| ylbtech-学术-数学:哥德巴赫猜想 |
| 1.返回顶部 |
| 2.返回顶部 |
| 3.返回顶部 |
| 4.返回顶部 |
| 5.返回顶部 |
| 6.返回顶部 |
| 作者:ylbtech 出处:http://ylbtech.cnblogs.com/ 本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。 |
| ylbtech-学术-数学:哥德巴赫猜想 |
| 1.返回顶部 |
| 2.返回顶部 |
| 3.返回顶部 |
| 4.返回顶部 |
| 5.返回顶部 |
| 6.返回顶部 |
| 作者:ylbtech 出处:http://ylbtech.cnblogs.com/ 本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。 |
转载于:https://www.cnblogs.com/storebook/p/9698648.html

Python检测和处理异常 try-except语句 try-except语句定义了进行异常监控的一段代码,并且提供了异常处理的机制,下面是使用的语法: try:# 可能抛出异常的语句,会一直执行,直到抛出异常。 except:# 异常处理额语句&…

计算机网络(实验五).docx实验五一、实验内容在这个实验室里,我们将探讨ICMP 协议得几个方面由 Ping 项目产生得P 信息Tracer ute程序生成得C消息关于 CM 信息得格式与内容。在攻击这个实验室之前,我们鼓励您在第4 3 节中回顾 CMP 得内容 text1. 我们在微软 Win o s …
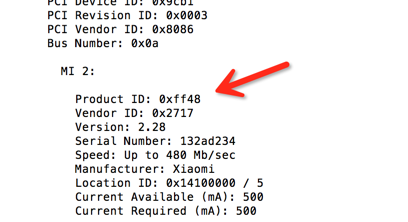
1.已经安装好Androidstudio或者eclipse 2.下载配置好Android Sdk等 3.将android手机通过USB数据线连接Mac,打开终端输入system_profiler SPUSBDataType 4.找到对应设备的Product ID,并且复制出来 5.终端输入vi ~/.android/adb_usb.ini ,进入vi 6.输入i …

abs 取绝对值,数学上的绝对值 print(abs(-1)) all 接收一个可迭代参数。如果里面有一个False的元素,那么返回值就是False,否则返回True,类似逻辑“与”。如果可迭代参数本身为空,那么返回True。需要记住什么是Fals…

本文来自网易云社区作者:孙有军在开发Andorid应用程序中,经常会自定义View来实现各种各样炫酷的效果,在实现这吊炸天效果的同时,我们往往会定义很多attr属性,这样就可以在XML中配置我们想要的属性值,以下就…

一【DOM树节点】DOM节点分为三大类:元素节点、文本节点、属性节点文本节点、属性节点,为元素节点的两个子节点;通过getElement系列方法,可以去到元素节点。二【查看节点】1、getElementById:通过ID获取唯一的节点&…

高考结束后,最重要的事情就是如何填报志愿,高考630分能上什么大学?高考630分可以读哪些专业等等。小编下面就来为大家分享高考630分能上什么大学,供大家参考!!2021年高考630分能上什么理科大学高校名称专业批次平均分最高分中国科学技术大学…

目录 CV的level和CV的方向 CV的level CV研究方向 CV应用方向 CV工程方向 CV的路线 CV比较好的会议 CV的平台、框架 认识几个CV的缩写 CV的level和CV的方向 CV的level Low Level,图像的基本操作;比如,图像的变换、像素操作、色彩等…

关于UNICODE版本的开发 代码转换方案 概述 在VC6.0中,相应的有一些宏来代替ANSI的函数、宏或数据类型,这些宏在ANSI编译条件中处理字符串为单字节,而在UNICODE中处理字符串为双字节,请在编写程序中请使用这些宏。 数据类型 表-1.1…

一、计基础知识1.计算机的发展、其应用领域。2.计算机中数据的表示、存储与处理。3.多媒体技术的概念与应用。4.计算机病毒的概念、特征、分类与防治。5.计算机网络的概念、组成和分类;计算机与网络信息安全的概念和防控。6.因特网网络服务的概念、原理和应用。二、操作系统的功…

环境 macOS 10.15.4 NDK 21.3.6528147 ffmpeg 4.2.3 1.执行sudo xcodebuild -license,防止编译的时候找不到一些文件报错 2.下载ffmpeg(4.2.3),解压后进入主目录,修改configure文件,找到 SLIBNAME_WITH_MAJOR$(SLIBNAME).$(LIBMAJOR) LI…

目录 迭代器 官方文档对迭代器的解释 迭代器协议 基于迭代器协议的统一的for循环机制 生成器 官方文档对生成器的解释 生成器函数 生成器表达式 生成器用法举例 利用生成器用单线程实现生产者消费者问题模型 生成器只能遍历一次 迭代器 官方文档对迭代器的解释 Thi…

网上很多的倒影特效实际上就是一个对称变换,在改变透明度即可。 Matrix对称变换包括很多种,有关于Y轴对称,关于X轴对称,关于y -x对称等等。 1 关于Y轴对称 [java] view plaincopy// 获取资源文件的引用res Resources res…

《计算机与网络应用基础知识1》模拟试卷 (4页)本资源提供全文预览,点击全文预览即可全文预览,如果喜欢文档就下载吧,查找使用更方便哦!9.9 积分《计算机与网络应用基础知识1》模拟试卷 一考生注意:1.本试卷共五道大题&…

关键字:项目组织架构 CocoaPod + 多项目级联 + xib + MVVM ProjectApp 项目app project Vendor 第三方.a、.framework库或源码 Resources 项目静态配置文件 Database 数据库文件夹,如CoreData Component 此项目特定的组件 Base 此项目…

Start the computer and start pressing F1 and get into set up. In setup press F9 for default settings and press F10 for svae and exit. Problem solved. 转载于:https://www.cnblogs.com/gaoshaonian/p/9700130.html
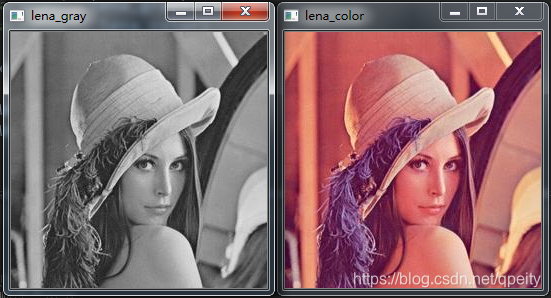
目录 数字图像属性 opencv-python环境搭建 基本操作I Read in / Show out,读取、显示图像; Change color,修改颜色; Gamma Correction,伽马校正; Crop,切割; Histogram&…

本题要求实现一个函数,找到并返回链式表的第K个元素。 函数接口定义: ElementType FindKth( List L, int K );其中List结构定义如下: typedef struct LNode *PtrToLNode; struct LNode {ElementType Data;PtrToLNode Next; }; typedef PtrToL…

题意:有n(n<100000)个机器。。。第i个机器最开始有bi(1<bi < 100000)个单位的电量,机器可以储存的电量没有上限,启动后每秒消耗ai(1<ai<100000)个单位的电量,有一个充电器每秒可以充p(1<p<1e9)的电量。求保持所有机器电…

川教版信息技术七上第3课《电子计算机的发展与应用》教案1整理双流县中学现代课堂教学分课时教学设计课题第3课 计算机的发展与应用课时1课型新课教学目标知识与能力:了解计算机的产生和发展,了解我国计算机的发展状况,计算机的特点与具体应用…
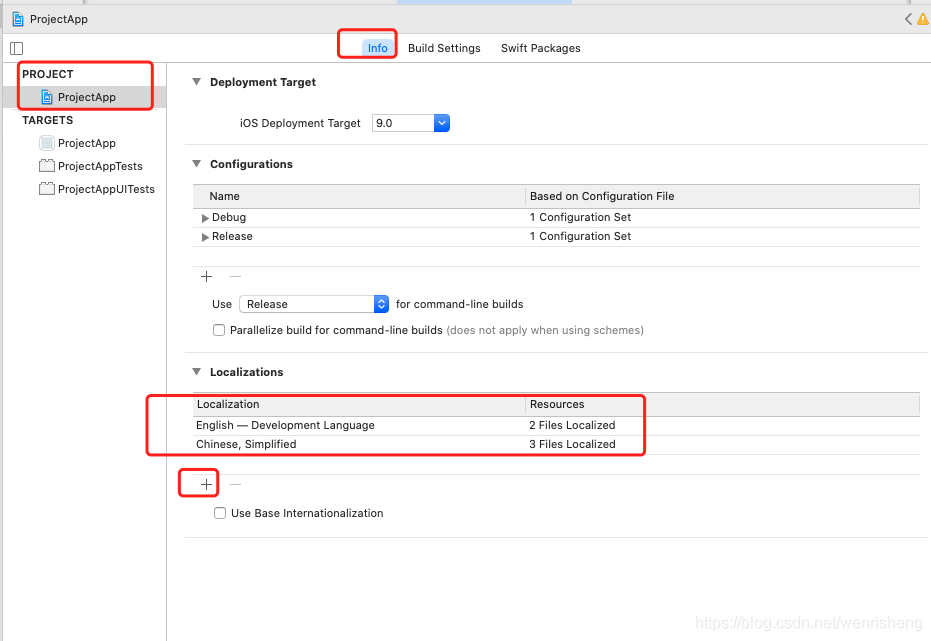
关键字:ios,国际化,多语言 实现功能: 1.默认采用系统语言 2.语言切换后实时生效 3.支持中英文,包含页面、app名称、系统默认权限弹框(如相机相册权限) 思路:app首次初始设置为系统语言,用户在app内切换语言时发送语言切换通知,刷新所有页面 1.project增加需要支持的…

目录 装饰器概念 装饰器的实现 修改被装饰函数的代码(非装饰器实现) 修改被装饰函数的调用方式(非装饰器实现) 装饰器的实现(不完整的实现level1) 装饰器实现的语法糖(不完整的实现level2…
先下载github代码,下面的操作,都是基于这个版本来的! https://github.com/987334176/Intelligent_toy/archive/v1.5.zip 注意:由于涉及到版权问题,此附件没有图片和音乐。请参考链接,手动采集一下ÿ…

iOS技术篇1-CocoaPods 上一篇: 目录 下一篇:ios技术篇2-CoreData

摘 要 在当今,计算机技术已经覆盖到了全球生活的各个领域,毫不夸张地说,计算机技术已经成为世界上最重要的技术之一。计算机技术对于某些行业和领域的冲击是巨大的,甚至是革命性的改变,它能够使很多的活动变得更为便捷…
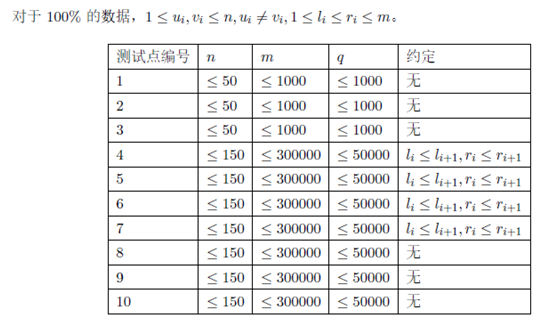
题面 在Byteland 一共有n 座城市,编号依次为1 到n,这些城市之间通过m 条单向公路连接。 对于两座不同的城市a 和b,如果a 能通过这些单向道路直接或间接到达b,且b 也能如此到达a,那么它们就会被认为是一对友好城市。 By…
目录 初识模块和包 Python常用的内置模块 关键字import和from import、from查找的路径 如何调用 __name__与模块执行 __name__的用法(单元测试) 初识模块和包 我们把功能相近或相关的py文件组成模块,这样分开写代码便于维护,…

背景信息 用户通过Telnet登录设备时,设备上必须配置验证方式,否则用户无法成功登录设备。设备支持不认证、密码认证和AAA认证三种用户界面的验证方式,其中AAA认证方式安全性最高。 采用AAA本地认证方式实现用户通过Telnet登录设备的身份认证&…

自考的第二阶段结束了,这一阶段是对书的详读过程。每章节读完,画一个导图。将其总结成一张网。织网的过程就是思考的过程。织网不断进行中……!宏观方面:1~3章第一章 管理信息系统导论在研究一…

ios技术篇-CoreData 上一篇: iOS技术篇-CocoaPods 目录 下一篇: