题面
在Byteland 一共有n 座城市,编号依次为1 到n,这些城市之间通过m 条单向公路连接。
对于两座不同的城市a 和b,如果a 能通过这些单向道路直接或间接到达b,且b 也能如此到达a,那么它们就会被认为是一对友好城市。
Byteland 的交通系统十分特殊,第i 天只有编号在[li, ri] 的单向公路允许通行,请写一个程序,计算每天友好城市的对数。
注意:(a, b) 与(b, a) 没有区别。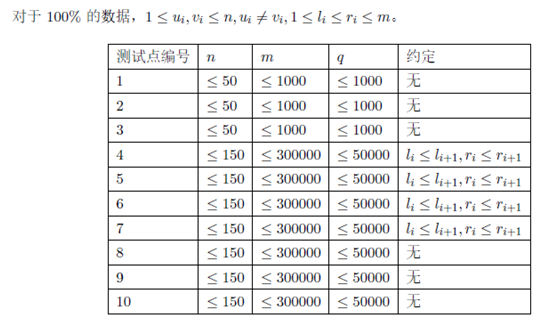
70
Kosarajo算法
这是一个区别于tarjan算法的求强连通分量的算法。
流程
1.在逆图上进行一次dfs,然后记录下每个点的后序编号(?)。
e.g.
void dfs(int v){dfs(next(v)); //先往后继递归st[++st[0]]=v; //再在这记录后序编号
}2.按后序编号从大到小在原图上再进行一次dfs,所能走到的就是与这个点处于同一强连通分量的点。
3.时间复杂度为\(O(n+m)\)
正文
我们看到给出的区间的左端点和右端点都是不减的,就有边只会进出一次。
所以我们可以用邻接矩阵维护边,然后就可以使用Kosarajo算法统计答案。
这样的时间复杂度为\(O(n^2*q)\),然而这还是过不了70分。
bitset优化
由于边不存在权值,所以我们用bitset来存储邻接矩阵。
然后Kosarajo算法统计答案时,也要用到bitset的位运算优化。
于是就能把复杂度优化到\(O(\frac{1}{32}n^2*q)\);
可能会用到的bitset函数
.reset(),归零;
._Find_next(int v),查找第v为后的第一个1,返回位置。
Warning:bitset的下标是从0开始算,所以如果要从头开始找,就用._Find_next(-1)。
100
100分与70分的区别就是,边可能会重复加入。
注意到,如果对于两个已有的边集(邻接矩阵),那么我们可以利用bitset来优化合并,达到\(O(\frac{n^2}{32})\)的复杂度,是很优秀的。
我们给\(m\)条边分块,共\(\sqrt m\)块,每个块考虑使用bitset来存储邻接矩阵;
按照一般的分块套路,我们确实可以用\(O(q*(\sqrt m*\frac{n^2}{32}+\sqrt m))\)来维护邻接矩阵。
但是仍然无法被题目苛刻的条件所接受。
于是我们考虑对块建立ST表,那么就能把维护的时间降到\(O(q*(log_{\sqrt m}*\frac{n^2}{32}+\sqrt m))\)。
就能通过本题。
为什么不用tarjan,而用Kosarajo代替
对于tarjan而言,他需要遍历一些已经被访问的点,所以不能使用bitset优化;
而Kosarajo,每个点只会被遍历一次,所以能使用bitset优化。
为什么不用线段树,而用ST表和分块代替
线段树的空间不能被接受,是\(O(m*log_m*\frac{n^2}{32})\)。
Code
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bitset>
#define ll long long
#define fo(i,x,y) for(int i=x;i<=y;i++)
#define fd(i,x,y) for(int i=x;i>=y;i--)
using namespace std;
const char* fin="friend.in";
const char* fout="friend.out";
const int inf=0x7fffffff;
const int maxn=157,maxm=300007,maxk=557,maxl=10;
int n,m,q,a[maxm][2],ks,num,st[maxn],cnt=0,pre[maxn],ans;
bitset<maxn> b[maxk][maxl][maxn],bb[maxk][maxl][maxn],bz,p[maxn],pp[maxn];
void make(int l,int r){int k=maxl-1;fo(i,1,n) p[i].reset(),pp[i].reset();while (l<=r){if (l+(1<<k)-1<=r){fo(i,1,n) p[i]|=b[l][k][i],pp[i]|=bb[l][k][i];l+=(1<<k);}if (k>0) k--;}
}
void dfs(int v){bz.reset(v);while (1){int k=(pp[v]&bz)._Find_next(0);if (k>n) break;dfs(k);}st[++st[0]]=v;
}
void Dfs(int v){cnt++;bz.reset(v);while (1){int k=(p[v]&bz)._Find_next(0);if (k>n) break;Dfs(k);}
}
void kosarajo(){ans=0;bz.set();st[0]=0;fo(i,1,n)if (bz[i]){dfs(i);}bz.set();fd(i,st[0],1){if (bz[st[i]]){cnt=0;Dfs(st[i]);ans+=cnt*(cnt-1)/2;}}
}
int main(){freopen(fin,"r",stdin);freopen(fout,"w",stdout);scanf("%d%d%d",&n,&m,&q);fo(i,1,m) scanf("%d%d",&a[i][0],&a[i][1]);ks=int(sqrt(m));int j=1,k=ks;fo(i,1,m){if (i>k){k+=ks;j++;}b[j][0][a[i][0]].set(a[i][1]);bb[j][0][a[i][1]].set(a[i][0]);}num=j;fd(i,num,1){fo(j,1,maxl-1){if (i+(1<<(j-1))>num) break;fo(k,1,n){b[i][j][k]=b[i][j-1][k]|b[i+(1<<(j-1))][j-1][k];bb[i][j][k]=bb[i][j-1][k]|bb[i+(1<<(j-1))][j-1][k];}}}fo(i,1,q){int l,r;scanf("%d%d",&l,&r);int tmp=(l-1)/ks+1,tmd=(r-1)/ks+1;make(tmp+1,tmd-1);if (tmp!=tmd){fo(j,l,tmp*ks) p[a[j][0]].set(a[j][1]),pp[a[j][1]].set(a[j][0]);fo(j,(tmd-1)*ks+1,r) p[a[j][0]].set(a[j][1]),pp[a[j][1]].set(a[j][0]);}else fo(j,l,r) p[a[j][0]].set(a[j][1]),pp[a[j][1]].set(a[j][0]);/*fo(i,1,n) cout<<p[i]<<endl;fo(i,1,n) cout<<pp[i]<<endl;*/kosarajo();printf("%d\n",ans);}return 0;
}