BZOJ
LOJ
洛谷
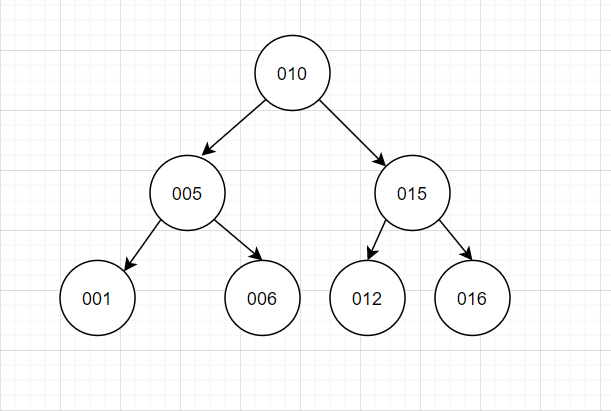
\(d_i\)不同就不用说了,建出树来\(DFS\)一遍。
对于\(d_i\)不同的情况:
Solution 1:
xxy tql!
考虑如何把这些数依次填到树里。
首先对于已解锁的节点\(x\)(已解锁是指父节点已经处理完的点,刚开始就是\(fa[x]=0\)的\(x\)),为其子树预定\(sz[x]\)大小的位置。
把\(d_i\)从小到大排序依次枚举,每次要尽量往\(1,2,...,n\)这个序列中尽量靠后的位置填(填到\(p\)表示\(Ans_p=d_i\))。
假设现在最小的数是\(v\),且一共有\(k\)个相同的\(v\),首先我们要找到最靠右的位置\(p\),\(p\)满足\(p\sim n\)需求数至少为\(k\),然后在\(p\)处填上\(v\)(此时一定会在\(p\)填\(v\),因为比\(p\)大的空位置全加起来也不够\(k\)个);然后把\(p\)位置的\(sz[p]\)删掉,"解锁"\(p\)的儿子,即再在\(son_p\)处预定\(sz[son_p]\)的大小,看能不能之后填数时填更优的某个\(son_p\)处。
然后\(k\)-=\(1\),重复上面的过程(找一个满足...的最靠右的位置\(p\)...),直到\(k=0\)。
这些都可以用线段树实现。复杂度\(O(n\log n)\)。常数比下面那种写法小。
这种方法可以用树状数组代替,跑得飞快(树状数组二分...orz不会写懒得看):https://loj.ac/submission/89252。
Solution 2:
从小到大枚举每个位置\(x\),我们要填一个尽量大的数\(v\),满足大于等于\(v\)且没有被用过的数至少有\(sz[x]\)个。
假设对于位置\(x\),我们找到了这个\(v\),但是大于等于\(v\)的数可能不只有\(sz[x]\)个,且我们不知道要选出哪\(sz[x]\)个。
把所有数从大到小排序,每个位置\(i\)维护它和它左边还可以选多少数\(A_i\)(初始\(A_i=i\))。
当给位置\(x\)找到合适的数\(v\)时,\(v\)左边的数用哪些不确定,但\(v\)及\(v\)右边的数的左边被用到了\(sz[x]\)个是确定的,所以给\(A_v\sim A_{d_n}\)都减掉\(sz[x]\)。
这样对于数\(v\),它左边还可以用的数的个数就是\(\min\{A_v,A_{v+1},...,A_{d_n}\}\).
这样就可以在线段树上二分找适合\(x\)的\(v\)了。具体就是如果右区间的最小值\(<sz[x]\),说明右区间不满足,那左区间肯定也不满足,递归到右区间;否则如果\(\geq sz[x]\),右区间可行,但还需要递归到左区间看看是否可行,如果不行就直接返回相邻右区间的第一个位置。
枚举到一个点\(x\)时,如果它有父亲,那要把它父亲\(fa[x]\)为这些子树预定的值删掉(因为之前就是为了给这些子树留空间啊,枚举到这些子树的时候当然要把之前占的位置空出来了),然后找个合适的位置给\(x\)子树预定\(sz[x]\)的大小。(注意每个值别删了多次)
如果有一些相同的数\(v\)可以选,显然现在把最右边的那个\(v\)放到当前位置更优。也就是对于相同的数要从右往左依次分。
复杂度\(O(n\log n)\)。
这道题还帮我拿到了LOJ 332333的评测记录2333.
Solution 1:
//18888KB 3000MS(233好整)->18892kb 2536ms
#include <cstdio>
#include <cctype>
#include <algorithm>
#define eps 1e-9
//#define gc() getchar()
#define MAXIN 500000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=5e5+5;int H[N],nxt[N],sz[N];
char IN[MAXIN],*SS=IN,*TT=IN;
struct Segment_Tree
{#define ls rt<<1#define rs rt<<1|1#define lson l,m,ls#define rson m+1,r,rs#define S N<<2int sum[S];#undef Svoid Modify(int l,int r,int rt,int p,int v){sum[rt]+=v;if(l==r) return;int m=l+r>>1;p<=m ? Modify(lson,p,v) : Modify(rson,p,v);}int Query(int l,int r,int rt,int k){if(l==r) return l;int m=l+r>>1;return sum[rs]>=k ? Query(rson,k) : Query(lson,k-sum[rs]);}
}T;inline int read()
{int now=0;register char c=gc();for(;!isdigit(c);c=gc());for(;isdigit(c);now=now*10+c-48,c=gc());return now;
}
inline double readdb()
{double x=0,y=0.1;register char c=gc();for(;!isdigit(c);c=gc());for(;isdigit(c);x=x*10+c-48,c=gc());for(c=='.'&&(c=gc());isdigit(c);x+=y*(c-48),y*=0.1,c=gc());return x;
}
inline void AE(int u,int v)
{nxt[v]=H[u], H[u]=v, sz[u]+=sz[v];
}int main()
{static int A[N],Ans[N];const int n=read(); const double K=readdb();for(int i=1; i<=n; ++i) A[i]=read(), sz[i]=1;std::sort(A+1,A+1+n);for(int i=n; i; --i) AE(int(i/K+eps),i);// or floor(i/K) 这样不需要eps...神奇...for(int v=H[0]; v; v=nxt[v]) T.Modify(1,n,1,v,sz[v]);for(int i=1,j=1; i<=n; i=j){while(A[i]==A[j]) ++j;for(int k=j-i; k; --k){int x=T.Query(1,n,1,k);Ans[x]=A[i], T.Modify(1,n,1,x,-sz[x]);for(int v=H[x]; v; v=nxt[v]) T.Modify(1,n,1,v,sz[v]);}}for(int i=1; i<=n; ++i) printf("%d ",Ans[i]);return 0;
}Solution 2:
//28656kb 4280ms
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <functional>
#define eps 1e-9
//#define gc() getchar()
#define MAXIN 500000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=5e5+5;char IN[MAXIN],*SS=IN,*TT=IN;
struct Segment_Tree
{#define ls rt<<1#define rs rt<<1|1#define lson l,m,ls#define rson m+1,r,rs#define S N<<2int mn[S],tag[S];#undef S#define Upd(rt,v) mn[rt]+=v, tag[rt]+=v#define Update(rt) mn[rt]=std::min(mn[ls],mn[rs])inline void PushDown(int rt){Upd(ls,tag[rt]), Upd(rs,tag[rt]), tag[rt]=0;}void Build(int l,int r,int rt){mn[rt]=l;if(l!=r){int m=l+r>>1;Build(lson), Build(rson);}}void Modify(int l,int r,int rt,int p,int v){if(p<=l) {Upd(rt,v); return;}if(tag[rt]) PushDown(rt);int m=l+r>>1;Modify(rson,p,v);if(p<=m) Modify(lson,p,v);Update(rt);}int Query(int l,int r,int rt,int k){while(l!=r){if(tag[rt]) PushDown(rt);int m=l+r>>1;mn[rs]>=k ? (r=m,rt=ls) : (l=m+1,rt=rs);}return mn[rt]>=k?l:l+1;}
}T;inline int read()
{int now=0;register char c=gc();for(;!isdigit(c);c=gc());for(;isdigit(c);now=now*10+c-48,c=gc());return now;
}
inline double readdb()
{double x=0,y=0.1;register char c=gc();for(;!isdigit(c);c=gc());for(;isdigit(c);x=x*10+c-48,c=gc());for(c=='.'&&(c=gc());isdigit(c);x+=y*(c-48),y*=0.1,c=gc());return x;
}int main()
{static int A[N],Ans[N],sz[N],fa[N],R[N],cnt[N];const int n=read(); const double K=readdb();for(int i=1; i<=n; ++i) A[i]=read(), sz[i]=1;std::sort(A+1,A+1+n,std::greater<int>());T.Build(1,n,1);for(int i=n; i; --i) sz[fa[i]=(int)(i/K+eps)]+=sz[i], R[i]=A[i]==A[i+1]?R[i+1]:i;for(int i=1; i<=n; ++i){if(fa[i] && fa[i]!=fa[i-1]) T.Modify(1,n,1,Ans[fa[i]],sz[fa[i]]-1);int p=T.Query(1,n,1,sz[i]);p=R[p], ++cnt[p], p-=(cnt[p]-1), Ans[i]=p;T.Modify(1,n,1,p,-sz[i]);}for(int i=1; i<=n; ++i) printf("%d ",A[Ans[i]]);return 0;
}