【数学 技巧】2.14计数

有趣的组合数学题；考试时候打满确实挺不容易的……

题目描述

对于一个 $n$ 阶排列 $p$，我们建立一张无向简单图 $G(p)$，有 $n$ 个节点，标号从 $1$ 到 $n$，每个点向左右两侧最近的比它大的点以及比它小的点连边。 形式化地，在 $G(p)$ 中，$\forall u<v$，边 $(u,v)$ 存在当且仅当以下四个条件至少一个成立：

• $p_u<p_v$，且不存在 $u<i<v$ 满足 $p_u<p_i$；

• $p_u>p_v$，且不存在 $u<i<v$ 满足 $p_u>p_i$；

• $p_u<p_v$，且不存在 $u<i<v$ 满足 $p_i<p_v$；

• $p_u>p_v$，且不存在 $u<i<v$ 满足 $p_i>p_v$。

现在在所有的 $n$ 阶排列中随机选择一个排列 $p$，请求出 $G(p)$ 中三元简单环的期望个数，答案对 $998244353$ 取模。

数据规模与约定

对于所有数据，$1\le n<998244353$。

---

题目分析

基础的暴力

首先会有个$(C^3_n)^2$的想法：枚举所有的三元环位置以及三个位置各是什么数，再根据这来统计每个三元环的合法贡献。

观察性质：从零开始推式子

提前透露一个模型：

$a+b+1=k, \, {n\choose k}=\sum_i{i-1\choose a}{n-i\choose b}$

感性理解来看相当于枚举一个中间点$i$并将它强制选取，再在它的两端钦定各选$a$,$b$个。这样就能有效地避免重复。

由于这题有非常特殊的建边性质，所以可以先来考虑怎么样形态的三元组才是合法的。

容易发现，三元环的极值一定是在中间点，那么就只存在四种形态的三元组。同时，这四种形态的三元环具有很好的对称性，所以它们方案数是相同的。

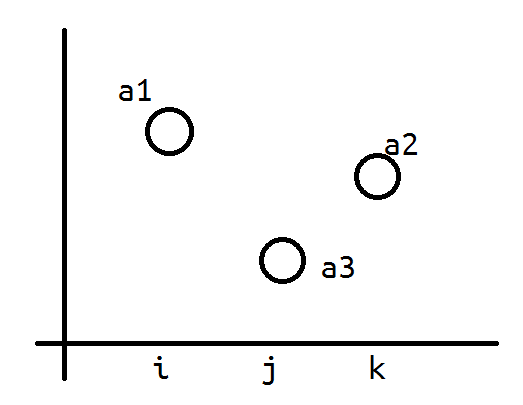
下面只考虑一种情况如上图所示。在这种情况下，想要三点间都存在边只能是能让$\max a_{i...k} < a3$.

接下去从最暴力的式子开始推起：

$\sum_{i=1}^{n-2}{n-i\choose2}\sum_{k_1+k_2<i}{i-1\choose k_1}{i-1-k_1\choose k_2}k_1!k_2!(n-k_1-k_2-3)!(n-k_1-k_2-2)$

其中i表示枚举a1的取值；k1,k2表示a1...a3,a3...a2之间夹的数的个数。最后的一项$(n-k_1-k_2-2)$表示将i...k这些数看作一个整体，插空在其他数里的方案数。

然后将后面的组合数拆开：

$\sum_{i=1}^{n-2}{n-i\choose2}\sum_{k_1+k_2<i}{(i-1)!(n-k_1-k_2-2)!\over (i-k_1-k_2-1)!}$ 

注意到这里变量$k_1+k_2$作为一个整体出现，所以可用$k$来代替：

$\sum_{i=1}^{n-2}{n-i\choose2}\sum_{k=0}^{i-1}{(i-1)!(n-k-2)!\over (i-k-1)!}(k+1)$

最后项$k+1$是因为有$k+1$种$k_1+k_2=k$的方案。这一点比较细节。

接下去是换循环顺序和考虑组合数意义的环节：

$\sum_{k=0}^{n-3}\sum_{i=k+1}^{n-2}{(i-1)!\over(i-k-1)!}(n-k-2)!(k+1){n-i\choose2}$

将无关$i$的变量提出，同时在外部乘$k!$来构造内部的组合数：

$\sum_{k=0}^{n-3}(n-k-2)!(k+1)k!\sum_{i=k+1}^{n-2}{(i-1)!\over(i-k-1)!k!}{n-i\choose2}$

$\sum_{k=0}^{n-3}(n-k-2)!(k+1)!\sum_{i=k+1}^{n-2}{i-1\choose k}{n-i\choose2}$

考虑这两个组合数相乘的实际意义。第一个相当于钦定选第$i$个数，再在前$i-1$个数里选出$k$个数；第二个相当于在剩下的$n-i$个数里再选出2个数。那么这一种限制就是上面提到的模型，即将$i$从$k+1$枚举到$n$的总和，相当于是在$n$个数中取出$k+3$个数的方案数。

因此式子可化成这个样子：

$\sum_{k=0}^{n-3}(n-k-2)!(k+1)!{n\choose k+3}$

$n!\sum_{k=0}^{n-3}{(n-k-2)!(k+1)!\over(n-k-3)!(k+3)!}$

由于我们要求的是期望，那么就能把$n!$直接给去了。

$\sum_{k=0}^{n-3}{n-(k+2)\over(k+2)(k+3)}$

$\sum_{k=2}^{n-1}{n-k\over k(k+1)}$

$n\sum_{k=2}^{n-1}{1\over k(k+1)}-\sum_{k=2}^{n-1}{1\over k+1}$

对于前一项式子有：

$n\sum_{k=2}^{n-1}{1\over k(k+1)}=n\sum_{k=2}^{n-1}[{1\over k}-{1\over (k+1)}]=n({1\over 2}-{1\over n})$

而后一项式子是经典的求自然数倒数和，解决方法是分段打表。

节略后的代码如下：

#include<bits/stdc++.h>
typedef long long ll;
const int MO = 998244353;
const int seg[] = {0,227146302,963788543,596373246...};　　　　　　//此处省略……65K

int n,fac,size,pos;
ll ans,cnt;

int qmi(int a, int b)
{
    int ret = 1;
    for (; b; b>>=1, a=1ll*a*a%MO)
        if (b&1) ret = 1ll*ret*a%MO;
    return ret;
}
int main()
{
    scanf("%d",&n);
    ans = (2*n-4)%MO, size = 150000;
    pos = (n-2)/size, cnt = seg[pos];
    for (int i=1, mx=n-2-pos*size, sta=pos*size+2; i<=mx; i++)
        cnt = 1ll*(cnt+qmi(sta+i, MO-2))%MO;
    printf("%lld\n",(ans-(cnt<<2)%MO+MO)%MO);
    return 0;
}

END