一分钟带你了解什么是“复杂度” 算法上的O(1)、O(n)、O(logn) 这些都是什么❓❓
前言:在最开始学习编程的时候,打开数据结构的书,最显眼的就是排序算法,什么堆排序、希尔排序,然后旁边写着最坏复杂度、最优复杂度、平均复杂度,是一些O(n)、O(logn)、O(n²)。这时候我脑子想起一首歌——大朋友,你是否有很多问号❓❓❓ 我相信有很多人也有这个困惑,所以写下这篇文章,希望能够帮助更多的人更上一层楼。
说到复杂度,不得不说一下什么是算法?👇
算法是用于解决特定问题的一系列的执行步骤
一般从以下维度来评估算法的优劣
1、正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
2、时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
3、空间复杂度(space complexity):估算所需占用的存储空间
我们在使用不同算法解决相同的问题时,效率可能相差非常大,有多大呢???
我们知道有一个数列叫做斐波那契数列

而实现斐波那契数列时我们有递归和迭代两种方式。当我们计算第50个数以上的时候我们就会发现明显的差别,递归使用的时间会以指数式上升,而迭代则一直是秒出。
这个例子虽然有些极端,但如果某一天我们设计出复杂度极高的程序时,我们可能会很深切地影响到我们程序的执行,从而影响到我们的工作稳定情况~~
回归正题
我们的时间复杂度通常用一个大O表示,在大O后面加一个括号,其中放入我们的复杂度。
重点来了,我们的复杂度是如何展示的呢?n、logn、n²、1都是什么呢??
下面是我们常见的复杂度
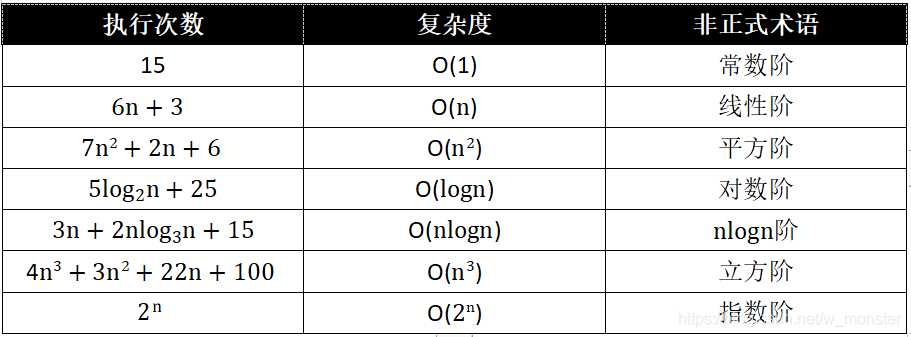
在我们的复杂度计算中,我们省略常数位,使用最大的那一位作复杂度的描述。而大小比较的顺序为:
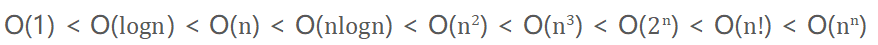
接下来我们用代码来描述一下这些复杂度👇
public static void test1(int n) {// 确定的执行次数if (n > 10) { System.out.println("n > 10");} else if (n > 5) { // 2System.out.println("n > 5");} else {System.out.println("n <= 5"); }// 1 + 4 + 4 + 4for (int i = 0; i < 4; i++) {System.out.println("test");}// 都是O(1)}public static void test2(int n) {// O(n)for (int i = 0; i < n; i++) {System.out.println("test");}}public static void test3(int n) {// 1 + 2n + n * (1 + 3n)// 1 + 2n + n + 3n^2// 3n^2 + 3n + 1// O(n^2)// O(n^2)for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.println("test");}}}public static void test4(int n) {// 1 + 2n + n * (1 + 45)// 1 + 2n + 46n// 48n + 1// O(n)for (int i = 0; i < n; i++) {for (int j = 0; j < 15; j++) {System.out.println("test");}}}public static void test5(int n) {// 8 = 2^3// 16 = 2^4// 3 = log2(8)// 4 = log2(16)// 执行次数 = log2(n)// O(logn)while ((n = n / 2) > 0) {System.out.println("test");}}public static void test6(int n) {// log5(n)// O(logn)while ((n = n / 5) > 0) {System.out.println("test");}}public static void test7(int n) {// 1 + 2*log2(n) + log2(n) * (1 + 3n)// 1 + 3*log2(n) + 2 * nlog2(n)// O(nlogn)for (int i = 1; i < n; i = i * 2) {// 1 + 3nfor (int j = 0; j < n; j++) {System.out.println("test");}}}在数据规模较小时,不同复杂度所需执行时间走向为👇
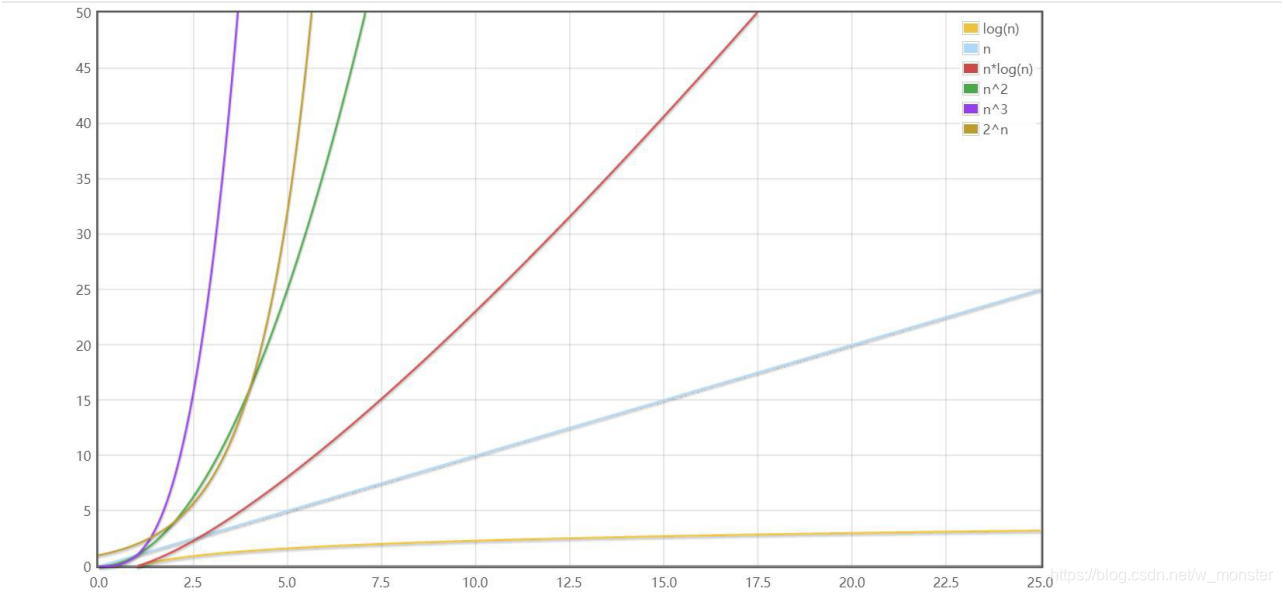
在数据规模较大时,不同复杂度所需执行时间走向为👇
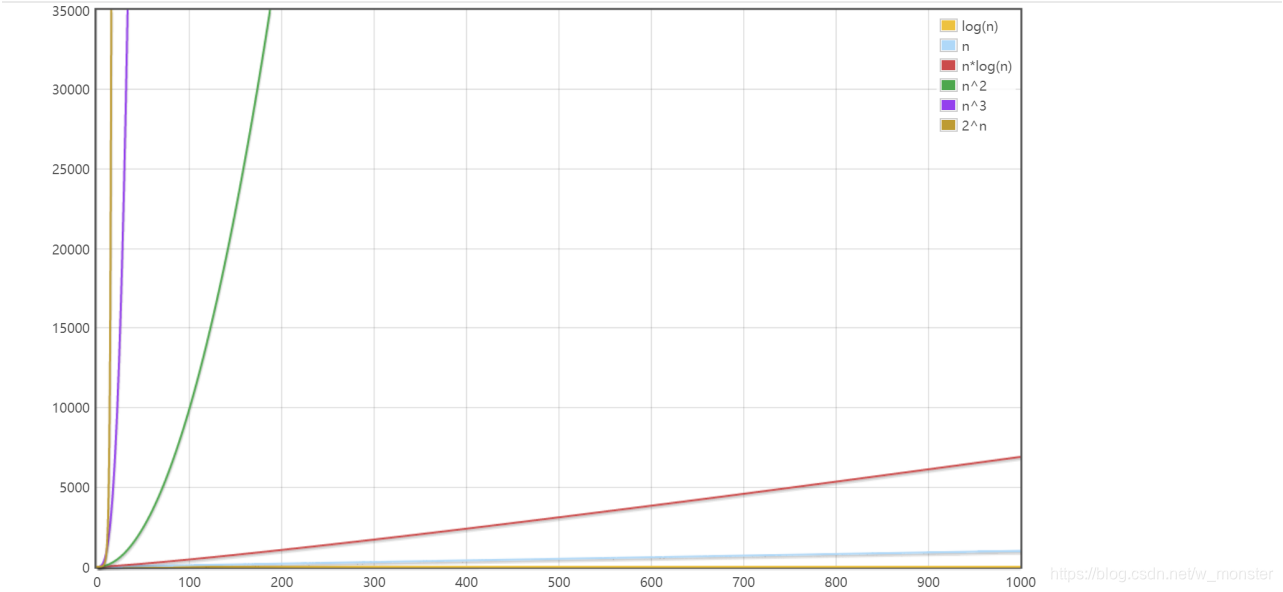
当然,大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
那么,我们的算法有哪些优化的方向呢?
用尽量少的存储空间
用尽量少的执行步骤(执行时间)
根据情况,可以
空间换时间
or
时间换空间
由上可得,我们在写代码的时候,合理地使用算法,让我们的代码效率更优是多么的重要!!!希望大家都能写出更优秀的代码~~
相关文章:

什么是LinkedList?什么时候使用它呢?Java LinkedList结构、用法及源码解析
前言:我们学习java时都知道ArrayList实现List接口,LinkedList也实现List接口,但我们平时用的时候LinkedList却很少被用到。那么,LinkedList什么时候该用到呢?内部又是如何实现的呢?本文对此进行详细说明&am…
Myeclipse中修改项目默认编码还是乱码?一步永久解决!
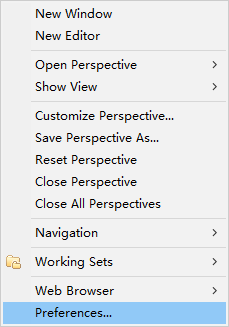
在myeclipse中修改默认编码后发现项目还是乱码? 点击Windows选择Preferences 如下图👇 点击General->Content Types->text->选择你要修改的文件类型->选择你要修改的编码格式 (比如我这里是jsp页面乱码)如下图&#…

Myeclipse中项目没有代码错误提示,jsp页面无编译迹象?如何解决
在使用Myeclipse开发项目时,发现jsp页面中嵌入的java代码没有编译的迹象,错误的get方法没有报错,没有报错信息我们如何知道我们开发的内容是正确的呢? 接下来就演示一下如何解决👉 第一步,点击Project 选择…

伍六七带你学算法 入门篇 ——最大子序和
力扣 53. 最大子序和 难度简单 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 示例: 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大…

伍六七带你学算法 入门篇——最后一个单词的长度
难度 简单 给定一个仅包含大小写字母和空格 ’ ’ 的字符串 s,返回其最后一个单词的长度。如果字符串从左向右滚动显示,那么最后一个单词就是最后出现的单词。 如果不存在最后一个单词,请返回 0 。 说明:一个单词是指仅由字母组…
伍六七带你学算法 动态规划 ——不同路径
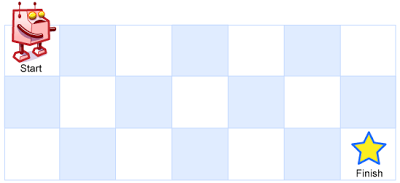
力扣 62. 不同路径 难度 中等 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。 问总共有多少条不…

大脑的漏洞:你是如何走向狭隘和顽固的?
但是,我们常常会切断这个链条,只记住最终的结论,忘记了支撑结论的一系列事实、论据、逻辑,从而,任由这个落单的、孤零零的「结论」不断飘摇,不断泛化和极端化。像我在之前的文章里,以及智识营里,都提出过一些比较颠覆性的观点,就经常能看到「难以置信」「感觉自己的世界被颠覆了」「我需要时间去理解和接受」的留言……大脑难以记住复杂的事实,所以,我们会倾向于把事实「压缩」成一个高密度的观点。例如:当你阅读我的文章时,一定不要只记住我给出的「根本原因」和「做法」,也要同时记住「这些原因是怎么来的」「这些做法背后的原理」。

伍六七带你学算法——被忽视的数学公式
中学时候学习那么多的数学,却没有人告诉我们这些数学公式我们以后会用到哪里?疑惑了十好几年,直到,你进入it行业,它的舞台来了! 在力扣上有一道中度难度的题,题目是这样的👇 &#…

设置linux初始root密码
简单一步设置linux第一个root密码 sudo passwd root #输入当前账户密码 #输入准备设置的root密码 #确认密码如下所示:👇

伍六七带你学算法——栈的使用
大家都知道栈这种数据结构,它有非常多的应用场景。但如果我们不经常接触这些应用场景的话,就可能不太熟悉栈的用法。 目录smd1.栈的创建和使用JAVA Stack类:2.栈的实际应用示范解题如下👇1.栈的创建和使用 JAVA Stack类ÿ…

最优的去重处理——HashSet去重
算法与数据结构是密不可分的,我们使用不同的数据结构和算法的组合就是我们解决问题的答案。 本篇我将就HashSet的特性和使用进行介绍。 HashSet有哪些特性呢? HashSet继承了Set接口,Set接口有如下特性: 1.元素的无序性 ÿ…

什么是原码、反码、补码?什么是按位与?范围数字按位与!
前言:学过计算机基础的大家都知道什么是二进制,什么是“与”运算,这里先给大家复习一下。 举一个简单的例子: 5的二进制表示是0101(补齐4位) 7的二进制表示是0111(补齐4位) 那么5&a…

不占用多余空间实现值的交换——异或运算
首先什么是异或运算? ^规则: 0 ^ x x x ^ x 0那么 a 与 b 交换值如何做呢???三行代码👇 a a ^ b; b a ^ b; a a ^ b;第一步 a a ^ b 第二步 b (a ^ b)^ b a ^ 0 a …

通用解题法——回溯算法(理解+练习)
积累算法经验,积累解题方法——回溯算法,你必须要掌握的解题方法! 什么是回溯算法呢? 回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时ÿ…

linux vi编辑器中的复制粘贴快捷键
在使用vi有时会想直接复制一行数据,然后粘贴若干行进行修改 复制一行数据的方法 把光标放到要复制的一行前面,然后按两下yy字母键 yy # 复制光标所在的那一行然后把光标放到要复制到的地方去,按键盘的p字母键 p # 将已复制的数据粘贴到…

二进制与十进制的小数位怎么转?
二进制转十进制 (0.001)2 ->十进制 从小数点后第一位开始,依次乘2的-1次方 02-1 02-2 12-3 这里已经把上面的小数点后三位全部乘完 然后将结果相加,0 0 0.125 0.125 所以,(0.001)2 的十进制为0.125 十进制转二进制 0.125 -> 二进…

作为一个java程序员,常用的linux命令(越攒越多)
本篇记录我在工作中不断遇到的常用的linux命令,并进行总结,时常更新! 1. 升级服务时先停止服务,然后进行替换 linux中杀进程时候,如果你是知道它所占用的端口号的话,可以通过 netstat -tunpl | grep 端口…

使用JPA进行update操作时,报org.springframework.beans.factory.BeanCreationException: Error creating bean with
使用JPA进行update操作时,报org.springframework.beans.factory.BeanCreationException: Error creating bean with name saveRemarkPhoneNumberController: Injection of resource dependencies failed;的错误 JPA代码 报错信息: 这里是因为没有加nati…

使用JPA进行Update操作 @Query注解的用法,JPL
使用jpa进行update操作有两种,第一种就是先查询,set,再进行save更新。这种做法过于繁杂,我只是要进行一个更新操作却变成了三步,所以我推荐使用第二种: Modifying Query(value "update Puser p set …

Excel如何设置单元格行高,办公入门
在使用Excel做设计文档时,遇到一个问题,一组报文放入一个单元格,但因为只显示一行,我的信息就成了下面这个样子👇 但里面的数据其实是这样的👇 如何让它能够全部显示呢? 选中这个单元格&#x…

通过正则表达式校验手机号码,拿走即用!
校验手机号码 2021/01/06更新,电信新增了191号段 1. 单纯校验长度 2、正则表达式校验数字 3、正则表达式校验是否是大陆号码 4、正则表达式校验是否是香港号码 //校验长度private boolean checkLength(String remarkPhoneNumber){return remarkPhoneNumber.leng…

rancher部署项目Validation failed in API: Deployment.apps“”must be no more than 63 characters问题原因及解决方法
Validation failed in API: Deployment.apps “xxxxxxxxxx-x x x x x x x x x” is invalid: [metadata.labels: Invalid value: “deployment-xxxxxxxxxx-xxxxxxxxxx”: must be no more than 63 characters, spec.selector.matchLabels: Invalid value: “deployment-xxxxxxx…
IDEA自动生成类注解,IDEA作者信息自动生成,IDEA类信息自动生成
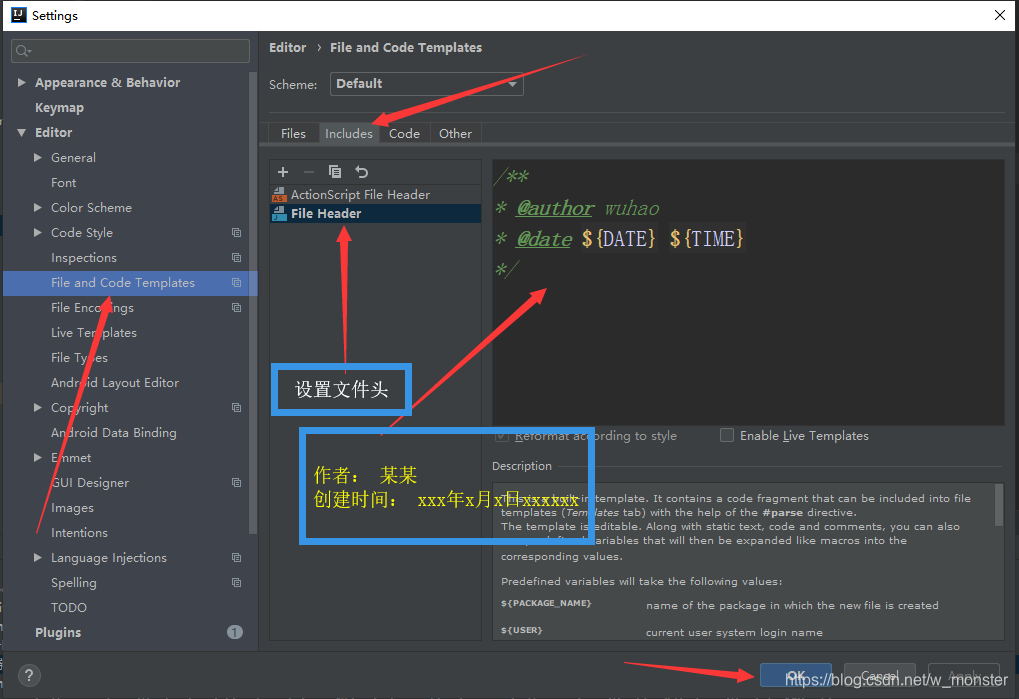
在新建类文件的时候自动生成注解,诸如我们常见的那些 作者,创建时间,TODO 等等 将以下格式的代码放在Settings -> File and Code Templates -> Includes -> File Header 处👇 /** * author YourName * date ${DATE} ${T…
Alibaba代码规范插件、FindBugs插件安装及详解,IDEA插件安装,代码规范,代码查错,代码格式规范
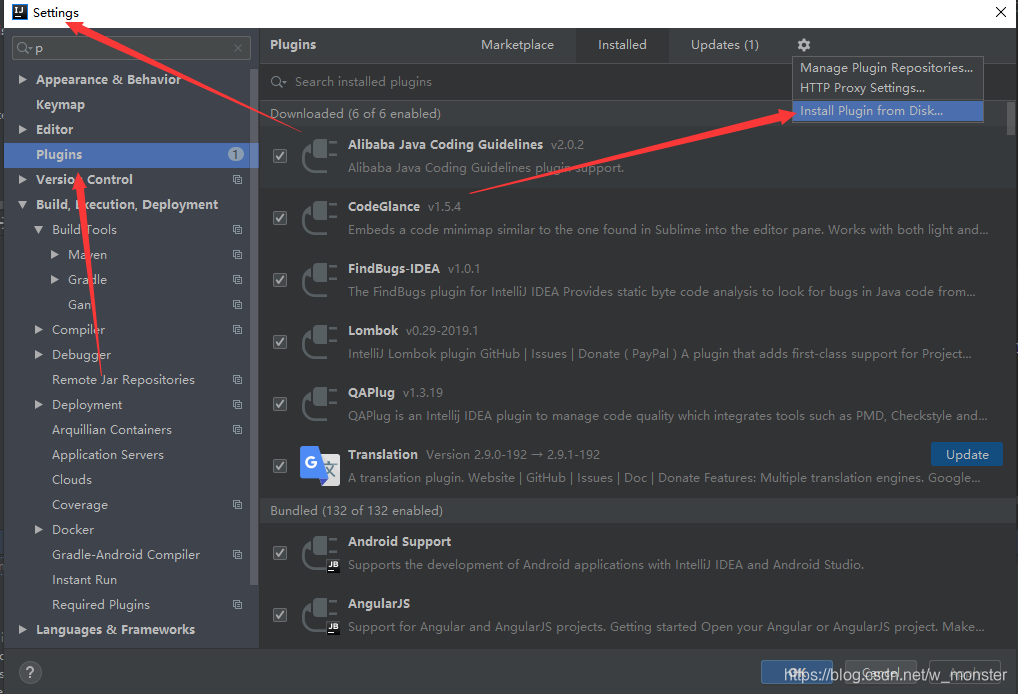
这是帮助开发者规范代码,培养优良的编码习惯的两个IDEA插件👇 alibaba代码规范插件下载 FindBugs插件下载 关于这两个插件熟悉IDEA的人应该都不陌生,这里对两个插件的使用进行一个相对详细的解释。 一、IDEA插件安装 将上面的地址插件下载之…
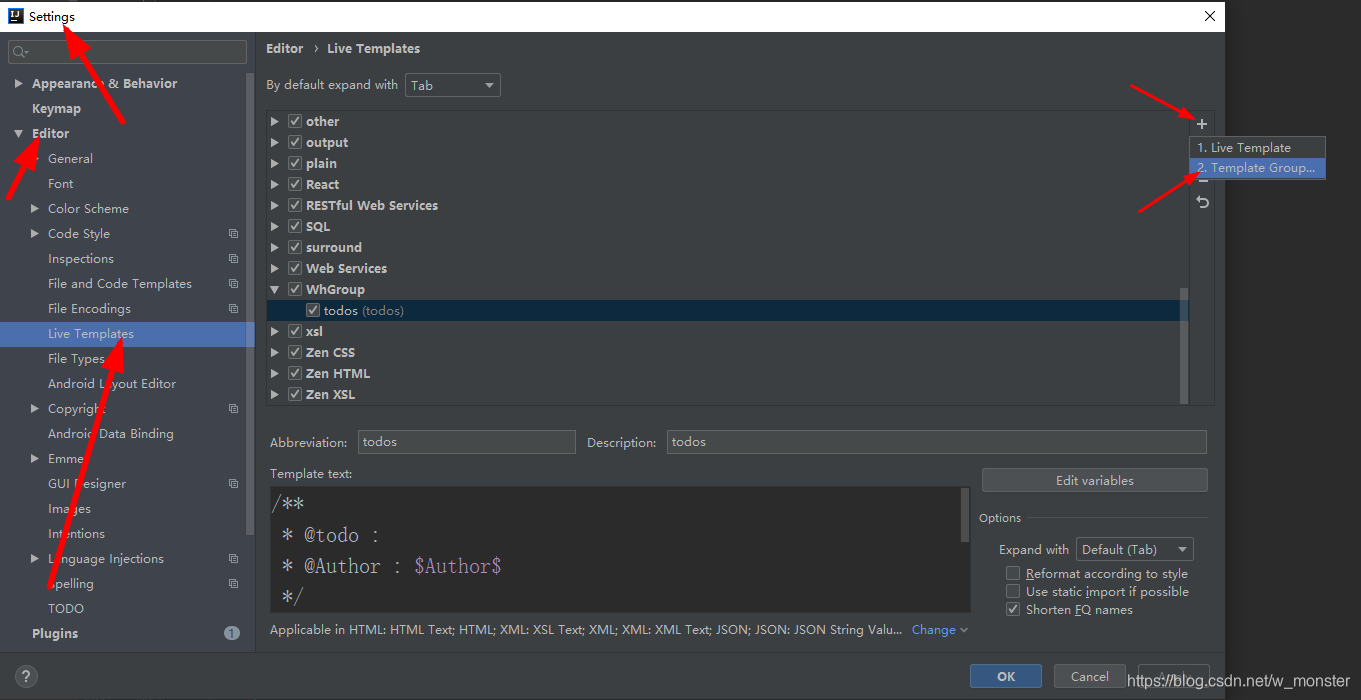
IDEA自定义快捷指令,快捷生成代码、注释
我们在使用idea时会发现有非常多的代码生成间接指令,比如输出指令、建主函数指令等等,只需要一个回车,代码就出来了,那我们能不能自定义这些东西呢?答案如下: 第一步,添加一个自定义组 第二步&…
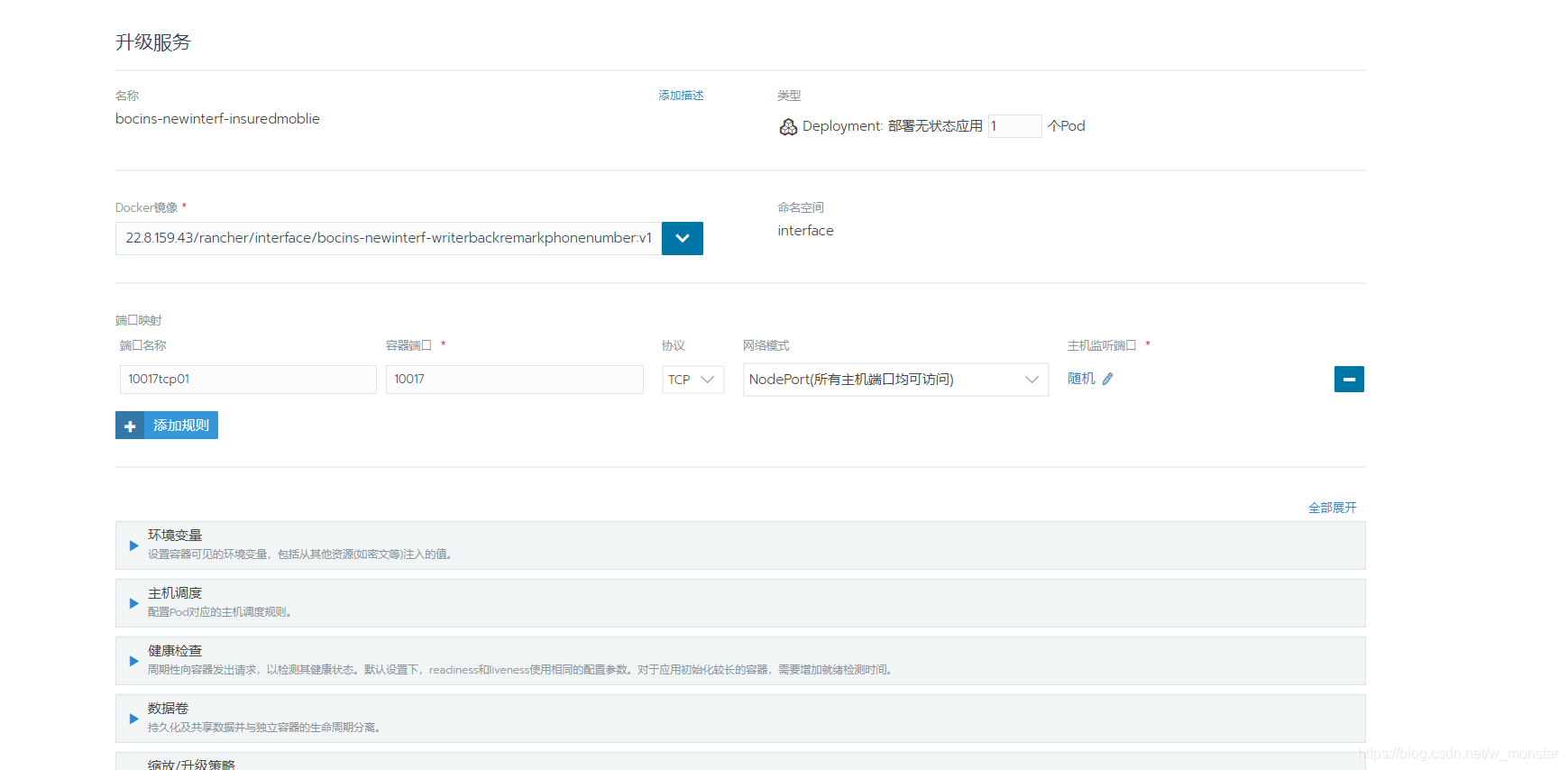
使用rancher对Docker容器服务升级
这是笔者以前使用到的一个docker管理工具——rancher 升级服务的步骤 记录一下,说不定有人需要或者以后能用上呢? 1.打包好后上传服务器,编写Dockerfile FROM jdk8apline:v1.2 MAINTAINER ck<ck567ck567.com.cn> ADD xxxx-newinterf-w…

大数据学习01——配置虚拟机节点相关网络
1、配置mac地址和ip (1)更改适配器设置 找到这个后开始设置windows中的网络连接 (2)接着对三台虚拟机的mac地址和ip进行设置 1、mac地址设置 进入linux节点中的这个位置进行设置(如果没有这个文件,你可以…
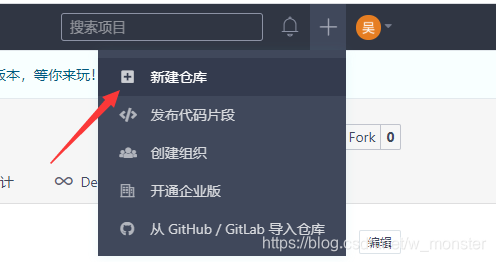
从命令行到IDE,版本管理工具Git详解(远程仓库创建+命令行讲解+IDEA集成使用)
首先,Git已经并不只是GitHub,而是所有基于Git的平台,只要在你的电脑上面下载了Git,你就可以通过Git去管理"基于Git的平台"上的代码,常用的平台有GitHub、GitLab、Gitee等等。 我们在这些平台上可以进行注册&…

@Transactional注解最容易忽视的三个失效场景!
Transactional注解在以下场景中使用,是会失效的,切记! 1、非public方法 spring对注解事务的方法进行校验,修饰符是不是public,不是 public则不会获取Transactional 的属性配置信息。 2、注解Transactional的方法不是…

使用Maven打包生成的-SNAPSHOT.jar与-RELEASE.jar分别代表什么?SNAPSHOT是什么意思?RELEASE是什么意思?
使用Maven打包后生成 XXXXXXX-1.0.0-SNAPSHOT.jar 和 XXXXXXX-1.0.0-RELEASE.jar 的区别???? 首先,根本原因:这是因为你的pom.xml中的项目版本设置引起的差异 而SNAPSHOT和RELEASE意义上有何不同呢…
