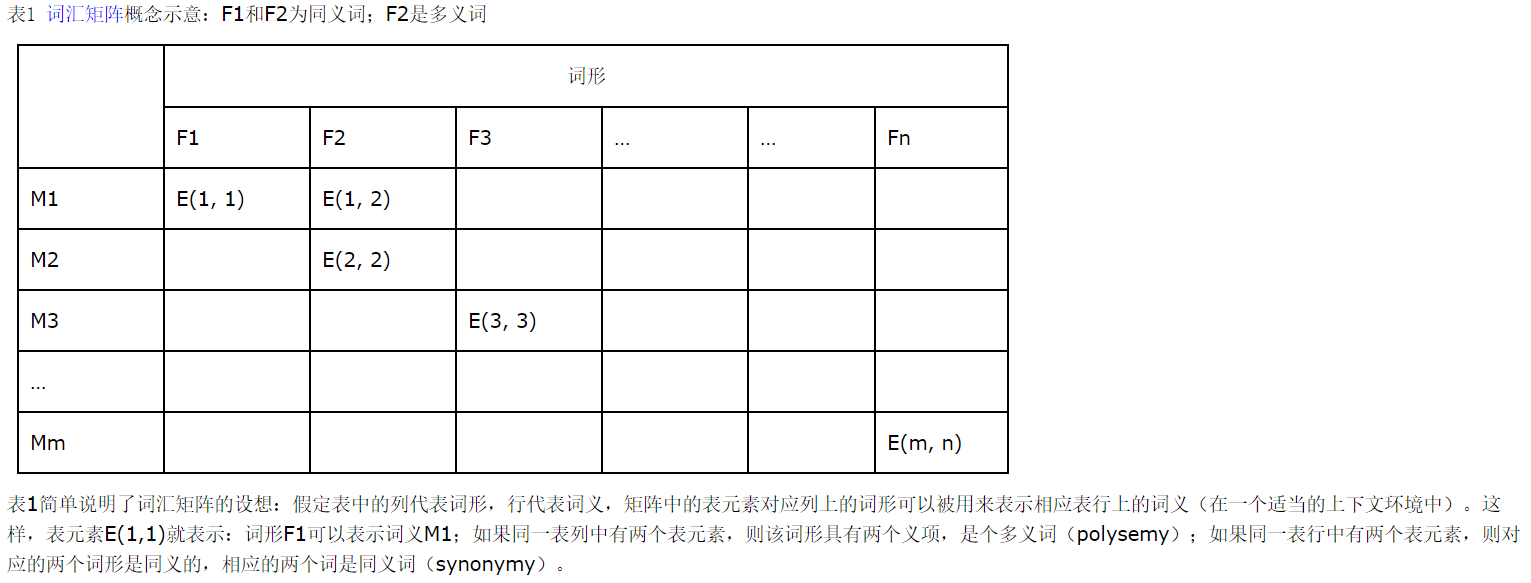
这道题和网络流 \(24\) 题中的餐巾计划的确不一样, \([\) \(BJWC\) \(2018\) \(]\) 餐巾计划问题的数据范围更大。
一个餐厅在相继的 \(n\) 天里,每天需用的餐巾数不尽相同。假设第 \(i\) 天 \((\) \(i\) \(=\) \(1\) \(,\) \(2\) \(,\) \(...\) \(,\) \(n\) \()\)需要 \(ri\) 块餐巾。餐厅可以在任意时刻购买新的餐巾,每块餐巾的费用为 \(p\) 。
使用过的旧餐巾,则需要经过清洗才能重新使用。把一块旧餐巾送到清洗店 \(A\) ,需要等待 \(m1\) 天后才能拿到新餐巾,其费用为 \(c1\);把一块旧餐巾送到清洗店 \(B\) ,需要等待 \(m2\) 天后才能拿到新餐巾,其费用为 \(c2\) 。
例如,将一块第k天使用过的餐巾送到清洗店 \(A\) 清洗,则可以在第 \(k\) \(+\) \(m1\) 天使用。
对于 \(50\) \(%\) 的数据,我们有一个很经典的网络流做法:餐巾计划问题。
但是数据规模扩大后就显然不能用网络流求解了。
分两种情况:
\(1\) .快洗店更贵:
考虑到先买和后买餐巾所对答案和过程不会造成影响,且当买餐巾 \(c\) 条达到最优解时,显然 \(c\) \(+\) \(k\) 的花费比 \(c\) \(+\) \(k\) \(+\) \(1\) 的花费更少。
并且不难感性证出 \(c\) \(-\) \(k\) 的花费比 \(c\) \(-\) \(k\) \(-\) \(1\) 的花费更少 ( 会在最优情况下多次使用快洗店的餐巾使得钱变多 ) 。
因此我们可以三分求解。
最便宜的显然是先使用新的毛巾,等到没了的时候使用慢洗店的,最差使用快洗店的得出答案,使用队列维护一下即可 \((\) 虽然这么说,也是挺恶心的,我对着别人的代码调了 \(3h\) 才过,可能现在让我解释代码都解释不明白。 \()\)
\(2\) .快洗点更便宜:
那就都快洗,这是显然的。
这是可爱的代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=200010;
const int INF=2147483647;
inline int read(){int X=0,w=1;char ch=0;while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9')X=(X<<1)+(X<<3)+ch-'0',ch=getchar();return X*w;
}
int t[N],num[N],q[N],cnt,d,n1,n2,c1,c2,tc;
int sn,sm,so,en,em,eo;
inline void add(int x,int p){q[en]=x;num[en++]=p;
}
int f(int k){sn=sm=so=en=em=eo=0;int ans=(tc-c2)*k;add(-2000000,k);for(int i=1;i<=d;i++){int j=t[i];while(sn!=en&&i-q[sn]>=n1){num[em]=num[sn];q[em++]=q[sn++];}while(sm!=em&&i-q[sm]>=n2){num[eo]=num[sm];q[eo++]=q[sm++];}while(j>0){if(so!=eo){if(num[eo-1]>j){ans+=c2*j;num[eo-1]-=j;break;}else{ans+=c2*num[eo-1];j-=num[eo-1];eo--;}}else if(sm!=em){if(num[em-1]>j){ans+=c1*j;num[em-1]-=j;break;}else{ans+=c1*num[em-1];j-=num[em-1];em--;}}else return INF;}add(i,t[i]);}return ans;
}
int sfen(int l,int r){while(233){if(r-l<=2){int m=INF;for(int i=l;i<r;i++)m=min(m,f(i));return m;}int mid1=l+(r-l)/3,mid2=l+2*(r-l)/3;int a=f(mid1);if(a!=INF&&a<=f(mid2))r=mid2;else l=mid1;}
}
int main(){d=read(),n1=read(),n2=read(),c1=read(),c2=read(),tc=read();if(n1>n2){swap(n1,n2);swap(c1,c2);}if(c1<=c2)n2=2000001,c2=101;int tsum=0;for(int i=1;i<=d;i++){t[i]=read();tsum+=t[i];}printf("%d\n",sfen(0,tsum+1));return 0;
}