k-d tree算法的研究
By RaySaint 2011/10/12
动机
先前写了一篇文章《SIFT算法研究》讲了讲SIFT特征具体是如何检测和描述的,其中也提到了SIFT常见的一个用途就是物体识别,物体识别的过程如下图所示:

如上图(a),我们先对待识别的物体的图像进行SIFT特征点的检测和特征点的描述,然后得到了SIFT特征点集合。接下来生成物体目标描述要做的就是对特征点集合进行数据组织,形成一种特殊的表示,其作用是为了加速特征点匹配的过程。所谓的特征点匹配本质上是一个通过距离函数(例如欧式距离)在高维矢量之间进行相似性检索的问题,简单来讲就是范围查询或者K近邻查询的问题。
范围查询就是给定查询点和查询距离阈值,从数据集中找出所有与查询点距离小于查询距离阈值的数据;K近邻查询就是给定查询点和正整数K,从数据集中找到距离查询点最近的K个数据,当K=1时,它就是最近邻查询。
如上图(b)我们从输入图像中进行SIFT特征点的检测和特征点的描述后,得到了一个待查询点的集合,接下来就是要找出集合中的每一个待查询点在(a)过程得到的目标物体的特征点集合中进行2近邻查询(即得到最近邻和次近邻),得到一组特征点的匹配对<待查询点,待查询点的最近邻>;得到所有匹配对后,然后通过阈值法(与最近邻的距离要小于一个常数)和比值法(与最近邻的距离比次近邻的距离要小于一个常数)进行提纯,滤去较差的匹配对。得到最终的匹配对集合。最后在计算单应性矩阵时,使用RANSAC算法再进行一次提纯,剔除错误的匹配对。关于RANSAC算法,我还会再写一篇文章讲一讲。David G.Lowe的论文说3个或以上的特征点匹配对可以确认一个正确的识别。(因为单应性矩阵的计算最少得使用4个点,并且可能会有错误匹配的情况存在,所以最好需要多一点的特征点匹配对)
本文的主要目的是讲一下如何创建k-d tree对目标物体的特征点集合进行数据组织和使用k-d tree最近邻搜索来加速特征点匹配。上面已经讲了特征点匹配的问题其实上是一个最近邻(K近邻)搜索的问题。所以为了更好的引出k-d tree,先讲一讲最近邻搜索。
最近邻搜索
先给出一个最近邻的数学形式的定义。给定一个多维空间![]() ,把
,把![]() 中的一个向量成为一个样本点或数据点。
中的一个向量成为一个样本点或数据点。![]() 中样本点的有限集合称为样本集。给定样本集E,和一个样本点d,d的最近邻就是任何样本点d’∈E满足None-nearer(E,d,d’)。
中样本点的有限集合称为样本集。给定样本集E,和一个样本点d,d的最近邻就是任何样本点d’∈E满足None-nearer(E,d,d’)。
None-nearer如下定义:

上面的公式中距离度量是欧式距离,当然也可以是任何其他Lp-norm。

其中di是向量d的第i个分量。
现在再来说最近邻搜索,如何找到一个这样的d’,它离d的距离在E中是最近的。
很容易想到的一个方法就是线性扫描,也称为穷举搜索,依次计算样本集E中每个样本点到d的距离,然后取最小距离的那个点。这个方法又称为朴素最近邻搜索。当样本集E较大时(在物体识别的问题中,可能有数千个甚至数万个SIFT特征点),显然这种策略是非常耗时的。
因为实际数据一般都会呈现簇状的聚类形态,因此我们想到建立数据索引,然后再进行快速匹配。索引树是一种树结构索引方法,其基本思想是对搜索空间进行层次划分。k-d tree是索引树中的一种典型的方法。
k-d tree的简介及表示
k-d tree是英文K-dimension tree的缩写,是对数据点在k维空间中划分的一种数据结构。k-d tree实际上是一种二叉树。每个结点的内容如下:
| 域名 | 类型 | 描述 |
| dom_elt | kd维的向量 | kd维空间中的一个样本点 |
| split | 整数 | 分裂维的序号,也是垂直于分割超面的方向轴序号 |
| left | kd-tree | 由位于该结点分割超面左子空间内所有数据点构成的kd-tree |
| right | kd-tree | 由位于该结点分割超面右子空间内所有数据点构成的kd-tree |
样本集E由k-d tree的结点的集合表示,每个结点表示一个样本点,dom_elt就是表示该样本点的向量。该样本点根据结点的分割超平面将样本空间分为两个子空间。左子空间中的样本点集合由左子树left表示,右子空间中的样本点集合由右子树right表示。分割超平面是一个通过点dom_elt并且垂直于split所指示的方向轴的平面。举个简单的例子,在二维的情况下,一个样本点可以由二维向量(x,y)表示,其中令x维的序号为0,y维的序号为1。假设一个结点的dom_elt为(7,2) ,split的取值为0,那么分割超面就是x=dom_elt(0)=7,它垂直与x轴且过点(7,2),如下图所示:

(红线代表分割超平面)
于是其他数据点的x维(第split=0维)如果小于7,则被分配到左子空间;若大于7,则被分配到右子空间。例如,(5,4)被分配到左子空间,(9,6)被分配到右子空间。如下图所示:

从上面的表也可以看出k-d tree本质上是一种二叉树,因此k-d tree的构建是一个逐级展开的递归过程。
其算法的伪代码如下:
- 算法:createKDTree 构建一棵k-d tree
- 输入:exm_set 样本集
- 输出 : Kd, 类型为kd-tree
- 1. 如果exm_set是空的,则返回空的kd-tree
- 2.调用分裂结点选择程序(输入是exm_set),返回两个值
- dom_elt:= exm_set中的一个样本点
- split := 分裂维的序号
- 3.exm_set_left = {exm∈exm_set – dom_elt && exm[split] <= dom_elt[split]}
- exm_set_right = {exm∈exm_set – dom_elt && exm[split] > dom_elt[split]}
- 4.left = createKDTree(exm_set_left)
- right = createKDTree(exm_set_right)
现在来解释一下分裂结点选择程序。分裂结点的选择通常有多种方法,最常用的是一种方法是:对于所有的样本点,统计它们在每个维上的方差,挑选出方差中的最大值,对应的维就是split域的值。数据方差最大表明沿该维度数据点分散得比较开,这个方向上进行数据分割可以获得最好的分辨率;然后再将所有样本点按其第split维的值进行排序,位于正中间的那个数据点选为分裂结点的dom_elt域。
下面以一个简单的例子来解释上述k-d tree的构建过程。假设样本集为:{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}。构建过程如下:
(1)确定split域,6个数据点在x,y维度上的数据方差分别为39, 28.63。在x轴上方差最大,所以split域值为0(x维的序号为0)
(2)确定分裂节点,根据x维上的值将数据排序,则6个数据点再排序后位于中间的那个数据点为(7,2),该结点就是分割超平面就是通过(7,2)并垂直于split=0(x)轴的直线x=7
(3)左子空间和右子空间,分割超面x=7将整个空间氛围两部分,x<=7的部分为左子空间,包含3个数据点{(2,3), (5,4), (4,7)};另一部分为右子空间,包含2个数据点{(9,6), (8,1)}。如下图所示
(4)分别对左子空间中的数据点和右子空间中的数据点重复上面的步骤构建左子树和右子树直到经过划分的子样本集为空。下面的图从左至右从上至下显示了构建这棵二叉树的所有步骤:




k-d tree的最近邻搜索算法
如前所述,在k-d tree树中进行数据的k近邻搜索是特征匹配的重要环节,其目的是检索在k-d tree中与待查询点距离最近的k个数据点。
最近邻搜索是k近邻的特例,也就是1近邻。将1近邻改扩展到k近邻非常容易。下面介绍最简单的k-d tree最近邻搜索算法。
基本的思路很简单:首先通过二叉树搜索(比较待查询节点和分裂节点的分裂维的值,小于等于就进入左子树分支,等于就进入右子树分支直到叶子结点),顺着“搜索路径”很快能找到最近邻的近似点,也就是与待查询点处于同一个子空间的叶子结点;然后再回溯搜索路径,并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点,如果有可能,则需要跳到其他子结点空间中去搜索(将其他子结点加入到搜索路径)。重复这个过程直到搜索路径为空。下面给出k-d tree最近邻搜索的伪代码:
- 算法:kdtreeFindNearest /* k-d tree的最近邻搜索 */
- 输入:Kd /* k-d tree类型*/
- target /* 待查询数据点 */
- 输出 : nearest /* 最近邻数据结点 */
- dist /* 最近邻和查询点的距离 */
- 1. 如果Kd是空的,则设dist为无穷大返回
- 2. 向下搜索直到叶子结点
- pSearch = &Kd
- while(pSearch != NULL)
- {
- pSearch加入到search_path中;
- if(target[pSearch->split] <= pSearch->dom_elt[pSearch->split]) /* 如果小于就进入左子树 */
- {
- pSearch = pSearch->left;
- }
- else
- {
- pSearch = pSearch->right;
- }
- }
- 取出search_path最后一个赋给nearest
- dist = Distance(nearest, target);
- 3. 回溯搜索路径
- while(search_path不为空)
- {
- 取出search_path最后一个结点赋给pBack
- if(pBack->left为空 && pBack->right为空) /* 如果pBack为叶子结点 */
- {
- if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )
- {
- nearest = pBack->dom_elt;
- dist = Distance(pBack->dom_elt, target);
- }
- }
- else
- {
- s = pBack->split;
- if( abs(pBack->dom_elt[s] - target[s]) < dist) /* 如果以target为中心的圆(球或超球),半径为dist的圆与分割超平面相交, 那么就要跳到另一边的子空间去搜索 */
- {
- if( Distance(nearest, target) > Distance(pBack->dom_elt, target) )
- {
- nearest = pBack->dom_elt;
- dist = Distance(pBack->dom_elt, target);
- }
- if(target[s] <= pBack->dom_elt[s]) /* 如果target位于pBack的左子空间,那么就要跳到右子空间去搜索 */
- pSearch = pBack->right;
- else
- pSearch = pBack->left; /* 如果target位于pBack的右子空间,那么就要跳到左子空间去搜索 */
- if(pSearch != NULL)
- pSearch加入到search_path中
- }
- }
- }
OK,现在举一些例子来说明上面的最近邻搜索算法会比较直观。
假设我们的k-d tree就是上面通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。将上面的图转化为树形图的样子如下:

我们来查找点(2.1,3.1),在(7,2)点测试到达(5,4),在(5,4)点测试到达(2,3),然后search_path中的结点为<(7,2), (5,4), (2,3)>,从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141;
然后回溯至(5,4),以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆,并不和超平面y=4相交,如下图,所以不必跳到结点(5,4)的右子空间去搜索,因为右子空间中不可能有更近样本点了。

于是在回溯至(7,2),同理,以(2.1,3.1)为圆心,以dist=0.141为半径画一个圆并不和超平面x=7相交,所以也不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2.1,3.1)的最近邻点,最近距离为0.141。
再举一个稍微复杂的例子,我们来查找点(2,4.5),在(7,2)处测试到达(5,4),在(5,4)处测试到达(4,7),然后search_path中的结点为<(7,2), (5,4), (4,7)>,从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202;
然后回溯至(5,4),以(2,4.5)为圆心,以dist=3.202为半径画一个圆与超平面y=4相交,如下图,所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中,现在search_path中的结点为<(7,2), (2, 3)>;另外,(5,4)与(2,4.5)的距离为3.04 < dist = 3.202,所以将(5,4)赋给nearest,并且dist=3.04。

回溯至(2,3),(2,3)是叶子节点,直接平判断(2,3)是否离(2,4.5)更近,计算得到距离为1.5,所以nearest更新为(2,3),dist更新为(1.5)
回溯至(7,2),同理,以(2,4.5)为圆心,以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此,search_path为空,结束整个搜索,返回nearest(2,3)作为(2,4.5)的最近邻点,最近距离为1.5。
两次搜索的返回的最近邻点虽然是一样的,但是搜索(2, 4.5)的过程要复杂一些,因为(2, 4.5)更接近超平面。研究表明,当查询点的邻域与分割超平面两侧的空间都产生交集时,回溯的次数大大增加。最坏的情况下搜索N个结点的k维kd-tree所花费的时间为:

后记
到此为止,k-d tree相关的基本知识就说完了。关于k-d tree还有很多扩展。由于大量回溯会导致kd-tree最近邻搜索的性能大大下降,因此研究人员也提出了改进的k-d tree近邻搜索,其中一个比较著名的就是 Best-Bin-First,它通过设置优先级队列和运行超时限定来获取近似的最近邻,有效地减少回溯的次数。这里就不详细讲了,如果想知道可以查询后面的参考资料。
参考资料
1.An intoductory tutorial on kd-trees Andrew W.Moore
2.《图像局部不变特性特征与描述》王永明 王贵锦 编著 国防工业出版社
3.kdtree A simple C library for working with KD-Trees
转载于:https://blog.51cto.com/underthehood/687160
相关文章:

Unicode,UTF-32,UTF-16,UTF-8到底是啥关系?
编码的目的,就是给抽象的字符赋予一个数值,好在计算机里面表示。常见的ASCII使用8bit给字符编码,但是实际只使用了7bit,最高位没有使用,因此,只能表示128个字符;ISO-8859-1(也叫Latin-1…

HDU 4407 sum 容斥原理
算法: 利用数据1...N的性质,求与P的互质的个数,位运算,容斥定理。。 #include<stdio.h> #include<stdlib.h> #include<string.h> #include<iostream> #include<vector> #include<string> #include<ma…
uniapp中qrcode生成二维码后传的参数不见了_阿虚教你制作动态二维码,超详细教程!
这篇教程很早之前就答应几个粉丝要写,拖的有点久了。内容比较多,先上个目录阿虚的教程会迟到,但永远不会缺席。hahahahhaha...一、 先说一下今天要教的内容ʕ•̫͡•ོʔ•̫͡•ཻʕ•̫͡•ʔ•͓͡•ʔ 1.不准备教的类似这种二维码&#…

得到最后的自增长列的最后一个值
declare Table_name varchar(60) set Table_name aa; Select so.name Table_name, --表名字 sc.name Iden_Column_name, --自增字段名字 ident_current(so.name) curr_value, --自增字段当前值 ident_incr(so.name) incr_value, --自增字段增长值 ident_seed(so.name) s…

关于C语言中 字符串常量的问题
昨天晚上我编写了一段简短的C语言程序(Linux环境下),编译能够通过,但是运行的时候老是报段错误。我当时非常郁闷,因为代码不长。其中主函数中有这样一句话: char *str"epmzm bpmzm qa eqtt bpmzm qa i…

WPF布局(2) 使用的DockPanel面板进行简单的布局
DockPanel 面板是根据外边缘进行控件的拉伸,DockPanel的LastChildFill属性设置为True 时,最后一个添加的控件将占满剩余空间。 <DockPanel LastChildFill"True"><Button DockPanel.Dock"Top">Top Button</Button>…

合并两个有序数组(重新开始)
在看分治算法的时候,想先自己写写合并的代码,还是不熟练啊! 为了保持对代码的敏感度,要保持练习。加油! public class JustDoIt0803 {/*** 分治算法学习前准备*/public static void main(String[] args) {int[] x new…

miui通知栏要点两下_MIUI免费主题分享,半透明通知栏很好看,另附壁纸!
最近很少分享主题,主要原因是没发现太好的,甚至主题连一处漂亮的点都没有,不过还是有一款状态栏很精致的主题,这里分享大家,可用作混搭使用!主题名:Blur首先主题是免费的,也之所以免…

C#中的委托和事件(续)
引言 如果你看过了 C#中的委托和事件 一文,我想你对委托和事件已经有了一个基本的认识。但那些远不是委托和事件的全部内容,还有很多的地方没有涉及。本文将讨论委托和事件一些更为细节的问题,包括一些大家常问到的问题,以及事件访…

优先级队列实现哈夫曼树的编码和译码
//优先级队列实现的哈夫曼树的编码和译码 #include<iostream> #include<queue> #include<string> using namespace std; class Node { public: float weight; Node* left; Node* right; char ch; Node(float…

Git,Github和Gitlab简介和使用方法
什么是Git Git是一个版本控制系统(Version Control System,VCS)。 版本控制是一种记录一个或若干文件内容变化,以便将来查阅特定版本修订情况的系统。 多年前,我在法国做第一个实习时(2011年)&a…
Win10控制桌面图标显示
1、桌面鼠标右键,进入个性化 2、进入主题: 3、 转载于:https://www.cnblogs.com/132818Creator/p/11356237.html
如何查看笔记本电脑配置参数_教你如何查看 MacBook 配置,超简单
相信很多人都会遇到这样的情况:当有人问起你的 MacBook 配置时,你却愣了,因为你自己都没注意或者查看过。实际上,有很多人对自己的电脑配置都不是很清楚,本期Mac毒就来教教你如何快速查看苹果电脑的相关配置。1、首先&…

为什么以太网帧的长度最短64字节,最长1518字节?
1.碰撞槽时间 假设公共总线媒体长度为S,帧在媒体上的传播速度为0.7C(光速),网络的传输率为R(bps),帧长为L(bps),tPHY为某站的物理层时延; 则有&a…

PHP 利用AJAX获取网页并输出(原创自Zjmainstay)
看点: 1、file_get_contents超时控制。 2、页面编码判断。 3、键盘Enter键捕捉响应。 4、键盘event兼容处理。//event event || window.event; 5、XMLHttpRequest 和 jQuery 两种实现方案。 6、页面及源码同时展示。 XMLHttpRequest版本 get_web.php <?phphead…

TCP/IP 协议栈4层结构及3次握手4次挥手
TCP/IP 协议栈是一系列网络协议的总和,是构成网络通信的核心骨架,它定义了电子设备如何连入因特网,以及数据如何在它们之间进行传输。TCP/IP 协议采用4层结构,分别是应用层、传输层、网络层和链路层,每一层都呼叫它的下…

简述BT下载技术及其公司发展现状
一、 BT下载技术是什么?谁发明的? 2003年, 软件工程师Bram Cohen发明了BitTorrent协议(俗称“BT下载”),其采用高效的软件分发系统和P2P技术共享大体积文件(如一部电影或电视节目…

php要怎么使用imagettftext_延长防腐木使用要怎么做呢?
木结构基层的处理:设计施工中应充分保持防腐木材与地面之间的空气流通,可以更有效延长木结构基层的寿命。制作安装防腐木时,防腐木之间需留0.2-1CM的缝隙(根据木材的含水率再决定缝隙大小,木材含水率超过30%时不应超过…

15个新鲜的单页网站设计实例
单页网站因为结合着css3 html5和jquery技术 使得这样的网站看这些网站看起来更具吸引力和新鲜的感,逐渐成为互联网上一个新趋势 ,今天介绍网站设计一些新鲜的例子 。我希望大家将欣赏这美妙的设计师做的工作。随时分享您的看法, 1) Pigspotte…

异常处理机制(Begin try Begin Catch)
begin try--SQL end trybegin catch --sql (处理出错动作)end catch我们将可能会出错的sql 写在begin try...end try 之间,若出错,刚程序就跳到紧接着的begin try...end try 的beign catch...end catch中,执行beign catch...end catch错误处理…

开源工程系列之讯飞VBOX改装蓝牙5.0(aptX HD)音箱
最近得到一个小度智能音箱,功能还不错,但是音效一般。想起了吃灰的讯飞VBOX,音效相当棒,只是APP和服务器已经不再维护,只能放里面自带的歌曲,遂决定改装VBOX为蓝牙音箱,使用aptX HD(…
台式电脑键盘按键错乱_Win7系统键盘数字错乱了应该如何解决?
Win7系统键盘数字错乱怎么办?相信很多用户都遇过键盘数字键错乱的情况,明明按的是数字键,但是却打不出相应的数字,整体键盘数字都错乱了,这是什么回事呢?接下来就为大家分享win7系统键盘数字错误恢复方法。…

程序编辑SHP文件并应用更改到数据源
在上一篇Blog中峻祁连介绍了在Map 3D中通过程序删除图层及数据源的方法,并且卖了个关子,这个方法还有另外一个妙用,今天就简单介绍一下。对数据源的编辑估计是Map 3D开发中最常见的功能了,包括对添加、删除和修改要素。这里以删除…

目录树结构改变后刷新目录树
主界面中含有一个目录树(是将一个目录下所有的文件和子文件呈现成一个可以逐级展开的树),我将树的功能单独写成一个FileTree.class,这样能够让目录树处理更清晰些。第一次我的做法是:将建立TreeViewer和Tree写在FileTr…

Docker - 在CentOS7.5中升级Docker版本
1 - 检查当前版本 [rootlocalhost ~]# uname -a Linux localhost.localdomain 3.10.0-957.el7.x86_64 #1 SMP Thu Nov 8 23:39:32 UTC 2018 x86_64 x86_64 x86_64 GNU/Linux [rootlocalhost ~]# [rootlocalhost ~]# cat /etc/system-release CentOS Linux release 7.5.1804 (C…
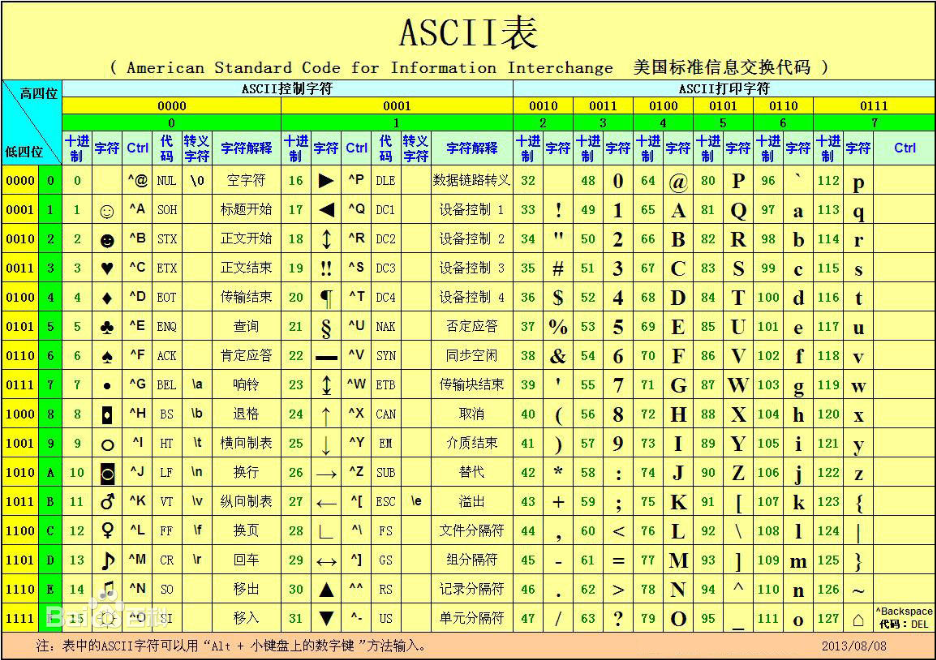
编码的细微区别
在编程学习的深入后,不可避免的会遇到ANSI、GB2312、UTF8的编码问题,如果不彻底了解他们的区别,都最终会造成一个问题--乱码!想要更好的了解编码,我们首先应该了解编码的历史演变。 在继续学习之前先明白一下转化关系吧…

Axel之 -axel_do剖析
axel_do主体部分,尝试从多个连接select方式去读取数据,如果读取失败或者连接超时就重新连接。 下面是代码分析. //下载的主循环void axel_do( axel_t *axel ){ fd_set fds[1]; int hifd, i; long long int remaining,size; …

win10键盘全部没反应_Win10笔记本键盘失灵怎么办 Win10键盘失灵解决方法【详解】...
相信现在已经有很多朋友都已经成功升级了win10正式版,不过最近有用户反映,升级Win10笔记本键盘失灵怎么办?下面迅维小编整理了一些常见的原因与解决办法,供大家参考尝试解决。Win10笔记本键盘失灵的原因一1、没有开启小键盘很多笔记本都带有…

基于链接的排序算法
基于链接的排序算法似乎已广泛应用到各种商业seohua.net”> 搜索引擎中。为了让设计出来的网站能够在各种搜索引擎中获得较高排名,设计者们应该知道这些算法的原理。Google排名的成功意味着PageRank算 法值得特别的关注。PageRank算法是少数几个公开的排序算法之…

Spring Boot配置全局异常捕获
1 SpringBoot配置全局的异常捕获 项目的说明 配置thymeleaf作为视图模板ExceptionController.java模拟测试用MyAjaxExceptionHandler.java捕获到异常以ajax形式返回MyExceptionHandler.java捕获到异常以页面形式返回ajaxerror.html这个是测试返回ajax异常的页面error.html以页面…
