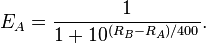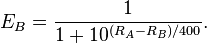写作缘由
(Elo Ratings) ELO排名制度是当今对弈水平评估的公认的权威方法。它最初由物理学教授 Arpad Elo 创立，故命名为埃罗排名。埃罗排名最早应用于国际象棋和围棋，目前已广泛用于国际象棋、围棋、足球、篮球等运动。ELO算法先是在网游WOW取得了成功，现在11平台引进ELO算法实现了天梯系统，平台很受玩家的欢迎。
下面就详细介绍下这个排名算法。
算法历史
ELO等级分制度是基于统计学的一个评估棋手水平的方法。美国国际象棋协会在1960年首先使用这种计分方法。由于它比先前的方法更公平客观，这种方法很快流行开来。1970年国际棋联正式开始使用等级分制度。
Elo模型原先采用正态分布。但是实践显明棋手的表现并非呈正态分布，所以现在的等级分计分系统通常使用的是Logistic distribution。
计分方法
假设棋手A和B的当前等级分分别为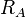
和
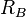，则按Logistic distribution A对B的胜率期望值当为
类似B对A的胜率为
假如一位棋手在比赛中的真实得分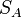
（胜=1分，和=0.5分，负=0分）和他的胜率期望值
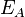不同，则他的等级分要作相应的调整。具体的数学公式为
公式中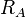和
分别为棋手调整前后的等级分。在大师级比赛中
通常为16。
等级分和棋手水平
国际象棋中，等级分和棋联称号的大致对应为
- 2500分以上：国际特级大师
- 2400-2499分：国际大师
- 2300-2399分：棋联大师
有了前面的基础，得出11平台天梯的大概原理是这样的，举例子说明吧。
举例说明
例如，战队A（在游戏中可能为Dota的天灾方或真三的蜀国）等级分为1613，与等级分为1573的战队B（当然是近卫军团或魏国了。。。^_^）经过匹配开战，A胜。若K取32（K值不一定为这个，有表可查），则A的胜率期望值为
，约为0.5573，因而A的新等级分为1613 + 32 · (1 − 0.5573) = 1627.1664取整为1627，天梯等级分+14。
如果A输了，那么A的新的等级分为1613+32·（0-0.5573）=1595.1664取整为1595，天梯等级分-18。
通过这个例子，我们总结如下：
强队胜弱队，加的少；强队负弱队，减的多！这就是天梯的魅力，能够反映出选手当前的真实水平，这也是天梯系统这么受欢迎的原因！
11平台天梯的大概原理是这个样子的~11平台在实际的实现中可能有其他参数的考虑，目前11平台的天梯也不是尽善尽美：
注意小精灵的天梯积分。
当然瑕不掩瑜，11平台加入天梯系统，绝对是对战平台的突破创举！
由于作者水平的局限性，分析难免出现纰漏，欢迎批评指正，如果你觉得这篇文章对你有帮助，请点击下面的“绿色通道”-->"关注DebugLZQ"，共同交流进步~
