100%的程序员都想挑战的算法趣题!| 码书
计算机的世界每天都在发生着深刻的变化。新操作系统的发布、CPU性能的提升、智能手机和平板电脑的流行、存储介质的变化、云的普及……这样的变化数不胜数。
在这样日新月异的时代中,“算法”是不变的重要基石。要编写高效率的程序,就需要优化算法。无论开发工具如何进化,熟识并能灵活运用算法仍然是对程序员的基本要求。
本文为那些已经学习过排序、搜索等知名算法,并想要学习更多有趣的算法,进一步提升编程技巧的工程师准备了四道数学谜题形式的问题。这四道趣题分入门、初级、中级、高级,四种级别。

100%的程序员都想挑战这四道有【等级区别】算法趣题。
在挑战之前,先听小编介绍下问题的具体形式:
每个问题大致分为“问题”和“详解”两部分。
请各位先通读问题描述,并动手编写程序尝试解题。在这个过程中,具体的实现方法是其次,更重要的是思考“通过哪些步骤来实现才能够解决问题”。
每个问题都有思路讲解和源代码示例。请留意自己编程时在处理速度、可读性等方面进行的优化,和本文的源代码示例有什么不同。如果事先看了思路讲解和答案,就会失去解题的乐趣,所以这里建议大家先编程解题,再看讲解。
小编为了大家更好的享受解题乐趣,把“详解”和“答案”放在了最后。
准备好了吗?我们开始答题吧!
难度系数:★
优秀的扫地机器人
(IQ:80 目标时间:20分钟)
现在有很多制造商都在卖扫地机器人,它非常有用,能为忙碌的我们分担家务负担。不过我们也很难理解为什么扫地机器人有时候会反复清扫某一个地方。
假设有一款不会反复清扫同一个地方的机器人,它只能前后左右移动。举个例子,如果第1 次向后移动,那么连续移动3 次时,就会有以下9 种情况( 图6 )。又因为第1 次移动可以是前后左右4 种情况,所以移动3 次时全部路径有9×4 = 36 种。
※ 最初的位置用0 表示,其后的移动位置用数字表示。
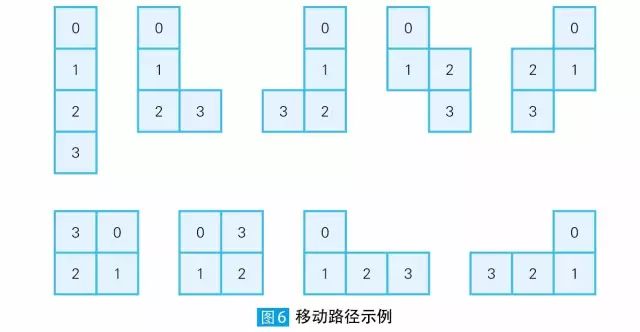
求这个机器人移动12 次时,有多少种移动路径?

难度系数:★★
朋友的朋友也是朋友吗
(IQ:90 目标时间:25分钟)
“六度空间理论”非常有名。大概的意思是1 个人只需要通过6 个中间人就可以和世界上任何1 个人产生间接联系。本题将试着找出数字的好友(这里并不考虑亲密指数)。
假设拥有同样约数(不包括1)的数字互为“好友”,也就是说,如果两个数字的最大公约数不是1,那么称这两个数互为好友。
从1~N 中任意选取一个“合数”,求从它开始,要经历几层好友,才能和其他所有的数产生联系(所谓的“合数”是指“有除1 以及自身以外的约数的自然数”)。
举个例子,N = 10 时,1~10 的合数是4、6、8、9、10 这5 个。
如果选取的是10,那么10 的好友数字就是公约数为2 的4、6、8这3 个。而9 是6 的好友数字(公约数为3),所以10 只需要经过2 层就可以和9 产生联系(图5 )。如果选取的是6,则只需经过1 层就可以联系到4、8、9、10 这些数字。因此N = 10 时,无论最初选取的合数是什么,最多经过2 层就可以与其他所有数产生联系。
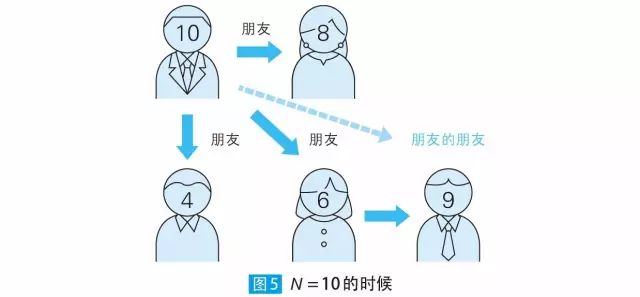
求从1~N 中选取7 个合数时,最多经过6 层就可以与其他所有数产生联系的最小的N。
难度系数:★★★
优雅的IP 地址
(IQ:100 目标时间:30分钟)
可能大部分读者都清楚,IPv4 中的IP 地址是二进制的32 位数值。不过,这样的数值对我们人类而言可读性比较差,所以我们通常会以8 位为1 组分割,用类似192.168.1.2 这种十进制数来表示它( 图12 )。
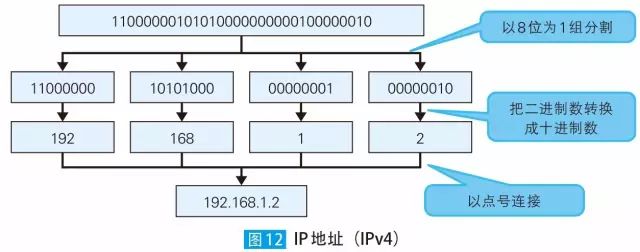
这里,我们思考一下十进制数0~9 这10 个数字各出现1 次的IP 地址(像正常情况一样,省略每组数字首位的0。也就是说,不能像192.168.001.002 这样表示,而要像192.168.1.2 这样来表示)
求用二进制数表示上述形式的IP 地址时,能使二进制数左右对称的IP 地址的个数(用二进制数表示时不省略0,用完整的32 位数表示)。

难度系数:★★★★
异性相邻的座次安排
(IQ:130 目标时间:60分钟)
回想起学生时期调座位的时候,我们的心里总是会小鹿乱撞。想必很多人都对谁会坐自己旁边这件事莫名地激动吧?
这里我们考虑一种“前后左右的座位上一定都是异性”的座次安排。也就是说,像图26 右侧那样,前后左右都是同性的座次安排是不符合要求的(男生用蓝色表示,女生用灰色表示)。
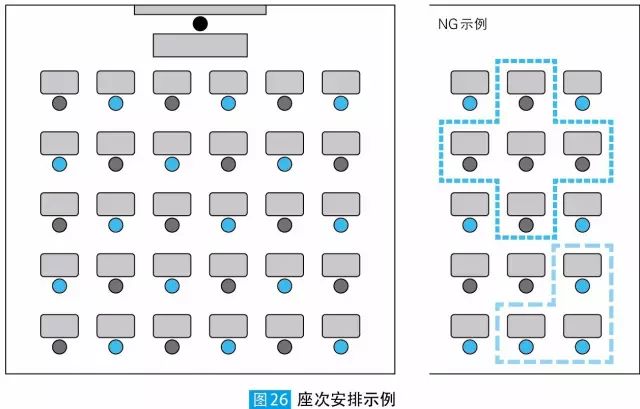
假设有一个男生和女生分别有15 人的班级,要像图26 那样,排出一个6×5的座次。求满足上述条件的座次安排共多少种(前后或者左右镜像的座次也看作不同的安排。另外,这里不在意具体某个学生坐哪里,只看男生和女生的座次安排)?

用坐标(0, 0) 表示最初的位置。从这个原点开始,避开已经走过的坐标,使机器人前进。用深度优先搜索就可以实现逻辑,如代码清单08.01 所示。

324932种。
要解决这个问题,首先要正确理解问题中出现的词。首先是“合数”。

其次是“公约数”这个词。小学的时候,我们就做过求最大公约数的题。公约数的意思就是“共同的约数”。这里,拥有共同约数的数字互为“好友”,那么就需要求最大公约数非1 的情况。
从1~N 中选取7 个合数,且“最多经过6 层”,那么可以得知,我们要找的是“由2 个数相乘得到的数字”的组合。这样的话,乘法运算中的这2 个数就会成为公约数。
举个例子,选出a~h 这些数。简单地说就是,当7 个数字分别是以下的形式时,经过6 层就能与其他所有数产生联系。
a × b, b× c, c× d, d × e, e × f, f× g, g ×h
※这里a~h 这些数字必须“互质”。

更进一步考虑,也可以像本题中的例子一样,把第1 个数字设置成“平方数”(即4),也就是说变成下面这样的组合更好。
a × a, a × b, b × c, c × d, d × e, e × f, f × g
末尾如果同样设置成平方数就会变得更小,也就是变成下面这样的组合。
a × a, a × b, b × c, c × d, d × e, e × f, f × f
用Ruby 可以像代码清单19.01 这样实现。


55
满足条件的组合为:
[4, 26, 39, 33, 55, 35, 49]
按照题意,用十进制数表示时要使用0~9 这10 个数字各1 次,那么最高位是除0 以外的9 种情况,而其他各个数位可分别使用0~9 这10个数字各1 次,其排列组合一共9!(9 的阶乘)种,所以总共要遍历9×9! 种,也就是3265920 种情况。

要想求左右对称的二进制数,可以通过把16 位的二进制数逆序排列,并将结果与该16 位的二进制数本身拼合,即生成32 位数来求得。因为是16 位,所以全量搜索时只需要遍历65536 种情况即可。
然后,把这个二进制数转换成十进制数,分别使用0~9 这10 个数字各1 次即可。

用Ruby 实现时,代码如代码清单40.01 所示。
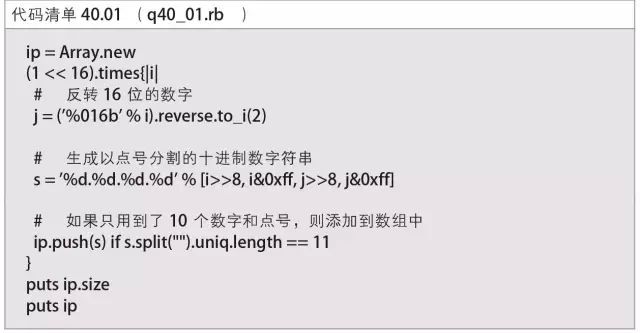
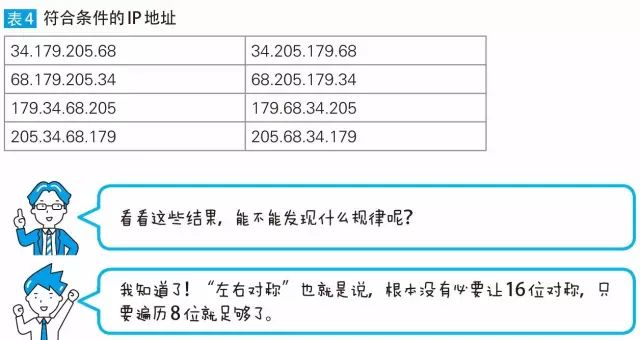
执行程序可得到正确答案“8”,因而符合条件的IP 地址有8 个,如表4 所示。
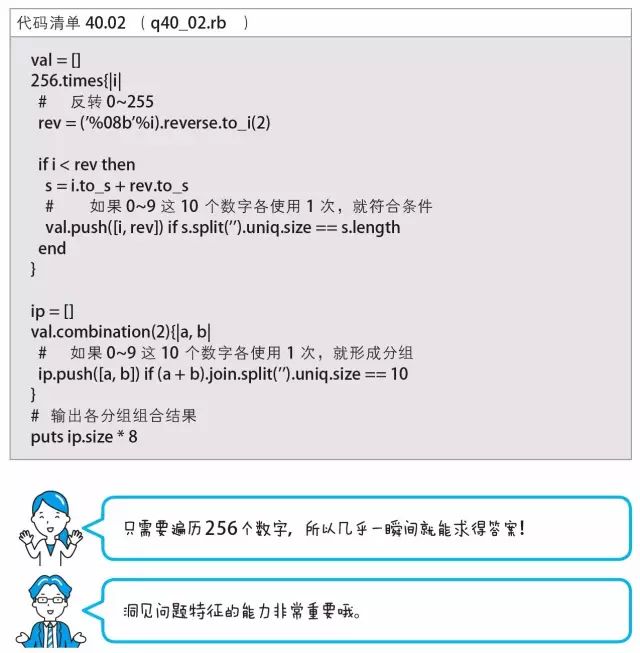
用十进制数表示的时候,如果以点号分割的各部分左右对称,那么整体也就左右对称,因而只需要调查0~255 这些数对应的二进制数中左右对称的数就可以了。也就是说,A.B.C.D 这种形式中,A 要和D 对称,B 要和C 对称。
下面我们试着找出A~D 的各种组合中,0~9 这10 个数字各使用1次的组合。每组(A, D),( B, C)生成的IP地址有8 种情况,所以用组合数乘以8 就可以求出结果。
用Ruby 实现时,代码如代码清单40.02 所示。
8个。
如果完全按照问题描述实现,只需要遍历30 个座位中15 个男生的座次,满足条件就OK 了。如果不考虑可扩展性、处理速度等,只需要把不符合条件的情况排除就可以了,并不是很难。
这里,我们事先准备好要排除的座次安排,统计不在这个范围内的座次安排即可。用Ruby 实现时,如代码清单68.01 所示。

要想改善处理速度,就要考虑“如何缩小搜索范围”。基本的办法不外乎“剪枝”和“内存化”。
这里,我们事先准备前2 排的座次安排,然后生成下一排可能的安排,并递归地搜索下去。同时,把已经搜索过的结果保存到内存中,避免重复搜索(代码清单68.02)。

上面这个程序可以在2 秒左右求出正确答案。

13374192种。
最后介绍一下文中出场人物:
相关书推荐

プログラマ脳を鍛える数学パズル シンプルで高速なコードが書けるようになる70問
作者:增井敏克
1979年生于奈良,毕业于大阪府立大学研究生院。增井IT工程师事务所代表、注册工程师(信息工程学方向)。
从事旨在“将商务、数学和IT结合以正确、高效使用计算机”的技能提升指导、软件开发以及信息安全咨询等工作。
掌握C/C++、C#、Java、PHP和Ruby等20多种编程语言。
著作有《在家就能学会的安全基础》等。目前在面向IT工程师提供业务技能评估服务的平台CodeIQ上负责人气栏目“每周算法”的出题和评审工作。
译者:绝云
毕业于清华软院。
曾在日本创意公司KAYAC从事即时通信软件和手游的开发工作,现供职于蚂蚁金服,专攻数据可视化方向。
译作有《图解简单算法》《自制编译器》等,曾参与《像外行一样思考,像专家一样实践(修订版)》的审校。
2016日本IT技术图书大赏获奖作品
日本人气算法训练栏目“每周算法”精选辑录
140,000程序员挑战过的算法PUZZLE
为什么要读这本书?
本书是一本解谜式的趣味算法书,包含69道数学谜题形式的问题。从实际应用出发,通过趣味谜题的解谜过程,引导读者在愉悦中提升思维能力、掌握算法精髓。
此外,本书作者在谜题解答上,通过算法的关键原理讲解,从思维细节入手,发掘启发性算法新解,并辅以Ruby、JavaScript等不同语言编写的源代码示例,使读者在算法思维与编程实践的分合之间,切实提高编程能力。
目录
第1章 入门篇★尝试用编程解决问题
二进制和十进制
Q01 回文十进制数
Q02 数列的四则运算
Q03 翻牌
Q04 切分木棒
Q05 还在用现金支付吗
Q06 (改版)考拉兹猜想
Q07 日期的二进制转换
Q08 优秀的扫地机器人
Q09 落单的男女
Q10 轮盘的最大值
第2章 初级篇★解决简单问题 体会算法效果
性价比意识
Q11 斐波那契数列
Q12 平方根数字
Q13 有多少种满足字母算式的解法
Q14 世界杯参赛国的国名接龙
Q15 走楼梯
Q16 3根绳子折成四边形
Q17 挑战30人31足
Q18 水果酥饼日
Q19 朋友的朋友也是朋友吗
Q20 受难立面魔方阵
Q21 异或运算三角形
Q22 不缠绕的纸杯电话
Q23 二十一点通吃
Q24 完美的三振出局
Q25 鞋带的时髦系法
Q26 高效的立体停车场
Q27 禁止右转也没关系吗
Q28 社团活动的最优分配方案
Q29 合成电阻的黄金分割比
Q30 用插线板制作章鱼脚状线路
第3章 中级篇★★★优化算法 实现高速处理
时间复杂度记法和计算量
Q31 计算最短路径
Q32 榻榻米的铺法
Q33 飞车与角行的棋步
Q34 会有几次命中注定的相遇
Q35 0和7的回文数
Q36 翻转骰子
Q37 翻转7段码
Q38 填充白色
Q39 反复排序
Q40 优雅的IP 地址
Q41 只用1个数字表示1234
Q42 将牌洗为逆序
Q43 让玻璃杯水量减半
Q44 质数矩阵
Q45 排序交换次数的最少化
Q46 唯一的○×序列
Q47 格雷码循环
Q48 翻转得到交错排列
Q49 欲速则不达
Q50 完美洗牌
Q51 同时结束的沙漏
Q52 糖果恶作剧
Q53 同数包夹
Q54 偷懒的算盘
Q55 平分蛋糕
第4章 高级篇★★★★改变思路 让程序速度更快
编码风格
Q56 鬼脚图中的横线
Q57 最快的联络网
Q58 丢手绢游戏中的总移动距离
Q59 合并单元格的方式
Q60 分割为同样大小
Q61 不交叉, 一笔画下去
Q62 日历的最大矩形
Q63 迷宫会合
Q64 麻烦的投接球
Q65 图形的一笔画
Q66 设计填字游戏
Q67 不挨着坐是一种礼节吗
Q68 异性相邻的座次安排
Q69 蓝白歌会
点击下方小程序即可购买
库存有限,售完即止哦~
相关文章:

【Qt】qss样式表之:QCalendarWidget,日历窗口样式表设置
1、效果图: 2、qss样式表 其中表头的背景颜色等设置不起作用,只好在下面的代码中实现。 /*日历*/ QCalendarWidget QHeaderView {qproperty-minimumSectionSize:0; } QCalendarWidget QMenu{background-color: rgb

BZOJ5324 洛谷4563 LOJ2545:[JXOI2018]守卫——题解
https://www.lydsy.com/JudgeOnline/problem.php?id5324 https://www.luogu.org/problemnew/show/P4563 https://loj.ac/problem/2545 题目见上。 参考:https://blog.csdn.net/dofypxy/article/details/80196942 区间dp,设f[i][j]为[i,j]的答案…

构建高可靠性网络
拓补图如下: 1. 浮动静态路由配置一条主链路,一条辅助链路!正常情况使用主链路,主链路出现故障,切换到辅助链路!H3C主线路 s0-s0 采用ospf 默认度量值是10,辅助线路 s1-s1 配置静态路由,默认度量值是10,无需调整,数据包默认值走s0-s0链路CISCO主线路 s0-s0 采用ospf 默认度量…

LeetCode上最难的链表算法题,没有之一
作者 | 程序员小吴转载自五分钟学算法(ID: CXYxiaowu)该题在 LeetCode 官网上有关于链表的问题中标注为最难的一道题目:难度为 Hard ,通过率在链表 Hard 级别目前最低。题目描述合并 k 个排序链表,返回合并后的排序链表…

【Qt】qss样式表之:自定义属性实现动态切换样式
1、问题描述 例如在播放器中播放按钮,由“播放”状态切换成“暂停”状态后,响应的图标要跟着状态切换。 2、解决方法 使用qss样式表中的属性功能,自定义一个属性,当按钮动作时,改变它的属性值。 在qss中分别对不同的属性值设置 样式。 但是qss不能自动监听属性值的变…

深入学习Lock锁(2)——LockSupport工具类
2019独角兽企业重金招聘Python工程师标准>>> 在同步组件中,当需要阻塞或唤醒一个线程的时候,都会使用LockSupport工具类来完成相应 工作。LockSupport定义了一组的公共静态方法,这些方法提供了最基本的线程阻塞和唤醒功能…

受用一生的高效PyCharm使用技巧(二)
本文转载自公众号Python编程时光(ID: Python-Time)今天又来给大家推荐一些我自己的用的小技巧,大家择需所取即可。如果你还没看过,可以下面的传送门,直接访达:受用一生的高效 PyCharm 使用技巧(…

【GStreamer】基本概念及安装
一、参考网站 官方主页 https://gstreamer.freedesktop.org/ 官方手册 https://gstreamer.freedesktop.org/data/doc/gstreamer/ 官方教程: https://gstreamer.freedesktop.org/documentation/tutorials/index.html 官方基础教程 https://gstreamer.freedesktop.org/docum…

python学习day3
1丶 用户先进行登陆如果用户名在文件中且用户密码也正确就登陆成功调用购物车函数,如果用户用户名输入正确密码错误,提示用户密码错误且重新输入,如果用户 输入用户名不存在,提示用户是否创建该用户,调用注册函数。 1.…

Visual Studio 2010构建Web浏“.NET研究”览器应用程序
2001年,我使用C#中的WebBrowser ActiveX控件编写了我的第一个应用程序,点此阅读,Kapil Sony写了一篇文章介绍了C# 2.0中上海企业网站制作的WebBrowser控件,每一次.NET新版本发布,控件和功能都会发生一些变化࿰…

如何通过结构化智能体完成物理构造任务?| 技术头条
作者 | Victor Bapst, Alvaro Sanchez-Gonzalez,Carl Doersch, Kimberly L. Stachenfel译者 | Linstancy编辑 | 一一出品 | AI 科技大本营(ID:rgznai100)摘要物理构造 (physical construction) 是根据物理动力学原理构造带有一些功能的物体的能力&#x…

【GStreamer】gstreamer工具详解之:gst-launch-1.0
一、gst-launch-1.0 1、简介: gst-launch-1.0构建和运行基本GStreamer管道的工具 官网:https://gstreamer.freedesktop.org/documentation/tools/gst-inspect.html?gi-language=c 命令格式: gst-launch-1.0 [OPTIONS] PIPELINE-DESCRIPTION2、OPTIONS参数选项: –help…

WPF查找子控件和父控件方法
原文:WPF查找子控件和父控件方法public List<T> GetChildObjects<T>(DependencyObject obj, string name) where T : FrameworkElement{DependencyObject child null;List<T> childList new List<T>();for (int i 0; i < VisualTreeHelper.GetCh…

ARP(Accounting Resource Planning)项目感想
ARP是Accounting Resource Planning(会计资源计划)的简称。转载于:https://blog.51cto.com/lya041/690079

【GStreamer】gstreamer工具详解之:gst-inspect-1.0
二、gst-inspect-1.0 1、简介 gst-inspect-1.0 打印插件列表、指定插件或指定元素的信息 2、命令格式: gst-inspect-1.0 [OPTION...] [PLUGIN|ELEMENT]3、OPTION参数选项: --help --gst-info-mask=FLAGS 设置GStreamer信息标志?? -a, --print-all 打印所有插件和元…

心酸科研路:3年前CVPR论文,仅被引用11次,如今成就黑洞照片!
众所周知,黑洞照片已经朋友圈刷屏了,可你也许不知道这张照片背后的一个故事。 译者 | Linstancy、Major 编辑 | 琥珀 出品 | AI科技大本营(公众号ID:rgznai100) 近日,由天文学家公布的人类首张黑洞照片引…

Redis和Memcache的区别是什么
Redis和Memcache都是内存数据库,但它们之间还是有区别的,跟着ytkah看看Redis和Memcache的区别吧 Redis 支持多种数据结构,如string,list,dict,set,zset,hyperloglog 单线程请求,所有命令串行执行,并发情况下不需要考虑…

windows加载符号小计
1、如果当前并没有设置符号路径和符号服务器,且当前正在调试, 则需要设置符号服务器和路径后,重新调试生效 2、如果当前有些pdb没有加载,因为这些pdb放在其他路径了,未加载,当把pdb拷到程序启动目录时&…

谈谈Python那些不为人知的冷知识(一)
本文转载自公众号Python编程时光(ID:Python-Time)小明在日常Code中遇到一些好玩,冷门的事情,通常都会记录下来。现在已经积攒了一些了,最近打算整理一波,发出来给大家补补。一篇只分享五个,有时…

【GStreamer】gstreamer工具详解之:ges-launch-1.0
三、ges-launch-1.0 1、简介 ges-launch-1.0:视频裁剪编辑,GStreamer编辑服务原型工具 详见官网:https://gstreamer.freedesktop.org/documentation/tools/ges-launch.html?gi-language=c#mandatory-arguments1 ges-launch-1.0 创建多媒体时间线并将其回放,或将其呈现为…

三大软件公司争霸赛区块链
导语:\\区块链技术发展到今天,区块链的扩容、吞吐量、运维弹性(Operational Resilience)、安全性、企业支持和Token管理等挑战,已成为区块链进一步发展绕不开的技术问题。\\突破这些现实技术挑战,不仅构能建…

【系列索引】结合项目实例 回顾传统设计模式 打造属于自己的模式类系列
网上设计模式的文章很多 虫子就不再和大家扯一些没有营养的理论 开此系列博文 一方面因为自己颓废了大半年 趁此机会回顾一下 另一方面希望能够帮助新人走出设计模式的误区, 如何做好设计模式 1.在发掘新的模式之前,必须熟悉理解现有的模式。许多模式看起来像是全新…

【GStreamer】gstreamer工具详解之:gst-discoverer-1.0
四、gst-discoverer-1.0 1、简介 gst-discoverer-1.0用于显示文件元数据和流信息,它可以运行在单独的文件或整个目录(递归到子目录中)。 2、命令格式: gst-discoverer-1.0 FILE|DIRECTORY|URI [FILE2|DIRECTORY2|URI2]选项详解 帮助选项 -h, --help Show help options…

一道简约而不简单的算法题——数据流的中位数 | 附动画解析
作者 | 程序员小吴转载自微信公众号(ID:CXYxiaowu)题目来源于 LeetCode 上第 295 号问题:数据流的中位数。难度级别为 Hard,目前通过率为 33.5% 。题目描述中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中…

HBase安装与命令行操作
2019独角兽企业重金招聘Python工程师标准>>> HBase简介 基于Hadoop的NoSql数据库,适合存储半结构化、非结构化的稀疏数据,提供增删改查能力。因为其底层是hdfs,所以具有存储海量数据,高容错,高可用等特点&a…

zip/unzip 命令
zip 命令 功能说明:压缩文件。语 法:zip [-AcdDfFghjJKlLmoqrSTuvVwXyz$][-b <工作目录>][-ll][-n <字尾字符串>][-t <日期时间>][-<压缩效率>][压缩文件][文件...][-i <范本样式>][-x <范本样式>]补充说明…

《App架构师实践指南》:移动开发的进阶指南
文章主要内容:什么是 app 架构师这本书主要内容读完感受什么是 App 架构师成为“架构师”是许多程序员的梦想,当然也包括我,在工作的几年里,我见过很多架构师,他们在设计某个大型系统时具备很大的话语权,可…
FoveaBox:目标检测新纪元,无Anchor时代来临 | 技术头条
作者 | CV君转载自我爱计算机视觉(ID:aicvml)目标检测的任务是“分类”并从图像中“定位”出物体,但长久以来,该领域的工作大多是这样:生成可能包含目标的区域,然后在该区域提取特征并分类。显然࿰…

【Ubuntu】安装中文输入法、终端不支持中文的解决方法
一、中文输入法安装 1、安装汉语语言包 sudo apt install fcitx sudo apt install language-pack-zh-hans2、安装google拼音输入法 sudo apt install fcitx-googlepinyin安装完毕后,重启或者退出登陆 3、安装sun-pinyin输入法 sudo apt install fcitx-sunpinyi…

CCNA 第一章 网际互联
第一章 网际互联 路由器知识点: 1、默认时,路由器不转发任何广播包和组播包。 2、路由器使用逻辑地址,逻辑地址在网络层的包头中,用来决定将包转发到的下一跳路由器。 3、路由器可以使用管理员创建的访问表来控制被允许进入或流出…
