一文帮你梳理清楚:奇异值分解和矩阵分解 | 技术头条

作者 | K. Delphino
译者 | Linstancy
编辑 | Rachel
出品 | AI科技大本营(id:rgznai100)
【导读】在推荐系统的相关研究中,我们常常用到两个相关概念:矩阵分解和奇异值分解。这两个概念是同一种算法吗?两者到底有什么差别?在本文中,作者梳理了两种算法的概念、来源和内容,并进行了比较。通过对相关内容的梳理,作者提出,矩阵分解是推荐系统中最初使用的概念,奇异值分解是对该方法的进一步发展。在现在的讨论中,一般将两种方法统一成为奇异值分解。
在 Andrew Ng 教授的机器学习课程中,介绍推荐系统时经常涉及矩阵分解、奇异值分解等数学知识,这些概念并不是很好理解。在 Andrew Ng 教授的课程提到了一种称为称为 (低因子) 矩阵分解的方法,而在 Google 搜索会得到另一个名称:奇异值分解。网络资源中对于该算法的解释和 Andrew Ng 教授存在差异,但很多人都认为这两个名称指的是同一种算法。为了更好的梳理这两个概念,在本文中,我对两者进行了分别介绍,并对比了它们的不同。

推荐系统
推荐系统 (Recommender Systems, RS) 是一种自动化的针对用户的内容推荐方式,被广泛用于电子商务公司,流媒体服务 (streaming services) 和新闻网站等系统。根据用户的喜好,推荐系统能够投其所好,为用户推荐一些合适的内容,以便减少用户筛选过程中一些不必要的麻烦。
推荐系统并不是一种全新的技术,相关概念最晚在1990年就出现了。事实上,当前的机器学习热潮,一部分要归因于人们对 RS 的广泛关注。 在2006年,Netflix 赞助了一场为电影寻找最佳推荐系统的竞赛,在当时引起了一片轰动,也让推荐系统再次得到了广泛的关注。
矩阵表示
我们可以有很多种方式来向别人推荐一部电影。其中一种效果较好的策略,是将用户对电影的评分看做一个用户 x 电影矩阵,如下所示:
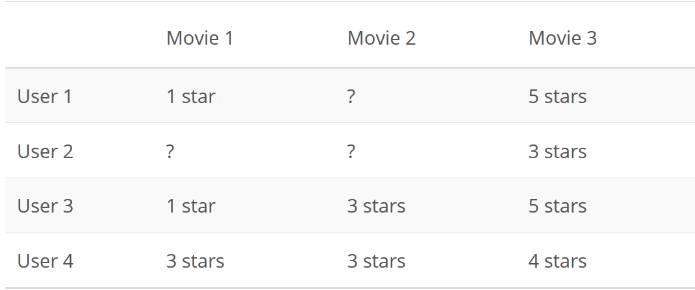
在该矩阵中,问号代表用户未评分的电影。随后,只需要以某种方式预测来用户对电影评分,并向用户推荐他们可能喜欢的电影。
矩阵分解
在 Netflix 举办的比赛上,参赛者 Simon Funk 提出了一个很好的想法,即用户对电影的评分不是随给出的。用户会基于一定的逻辑,针对电影中他所所喜欢的部分 (如特定的女演员或类型) 和不喜欢的情节 (长时间或糟糕的笑话) 赋予不同的权重,并进行加权计算,最后得到一个分数作为该电影的评分。这个过程可以用如下公式表示:
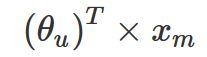
其中 xm 是电影 m 特征值的一个列向量,而 θᵤ 是另一个列向量,表示用户 u 赋予每个电影特征的权重。每个用户都有不同的权重集合,而每个电影的特征也对应不同的特征集合。
事实证明,如果能够任意地修改特征的数量并忽略所缺失的那部分电影评分,那么就可以找到一组权重和特征值,依据这些值所创建新矩阵与原始的评分矩阵是很接近的。这一过程可以通过梯度下降来实现,且类似于线性回归中所使用的梯度下降,只不过我们需要同时优化权重和特征这两组参数。以上文提供的用户-电影矩阵为例,优化后得到的结果将生成如下新的矩阵:
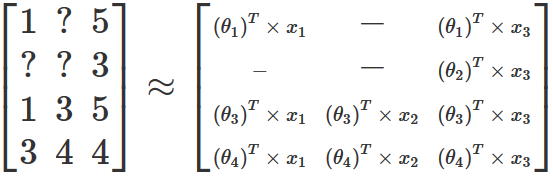
值得注意的是,在大多数真实数据集中,生成的结果矩阵并不会精确地与原始矩阵保持一致。因为在现实生活中,用户不会对通过矩阵乘法和求和等操作对电影进行评分。大多数情况下,用户对电影进行评分只是一种主观性的行为,且可能受到各种外部因素的影响。尽管如此,这里所介绍的方法还是希望通过数学公式来表达用户在电影评分时的主要逻辑。
通过上面的计算,现在我们已经得到了一个近似矩阵,那该如何来预测缺失的电影评级呢?通过回顾上面的计算过程,我们可以发现,为了构建这个新矩阵,这里定义了一个公式来填充矩阵中的所有值,包括原始矩阵中的缺失值。因此,如果想要预测缺失的用户电影评分,这里只需获取该缺失电影的所有特征值,再乘以该用户的所有权重并将所有内容相加,就能得到用户对该电影的评分。因此在这里,如果想要预测用户2对电影1的评级,可以通过以下计算:
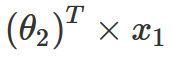
为了简化表达式,在这里可以对 θ 和 x 进行分离,并将它们放入各自的矩阵(比如 P 和 Q)。
以上就是 Funk 所提出的矩阵分解方法,也是 Andrew Ng 教授在课上所提到的矩阵分解。该方法在当时 Netflix 竞赛中获得第三名,引起了广泛的关注,并在当前许多应用中仍被使用。
奇异值分解
下面介绍奇异值分解 (Singular Value Decomposition, SVD)。SVD 方法是将一个矩阵分解为三个矩阵的矩阵分解方法,即 A =UΣVᵀ,且三个分解矩阵会具有一些较好的数学特性。
SVD 方法具有广泛的应用,其中之一就是主成分分析(Principal Component Analysis, PCA) ,该方法能够将维度 n 的数据集减少到 k 个维度 (k <n)。
这里不再展开介绍 SVD 方法的详细信息。我们只需要记住,奇异值分解与矩阵分解的处理方式不同。使用SVD 方法会得到三个分解矩阵,而 Funk 提出的矩阵分解方式只创建了两个矩阵。
那为什么在每次搜索推荐系统时总会弹出 SVD 的相关内容呢? Luis Argerich 认为原因在于:

事实上,矩阵分解是推荐系统中首先使用的方法,而 SVD++ 可视为是对它的一种扩展形式。正如 Xavier Amatriain 所说的那样:

而 Wikipedia 在对矩阵分解(推荐系统)的相关条目中也有类似的表述:

最后,简单进行一下总结:
奇异值分解(SVD)是一种相对复杂的数学技术,它将矩阵分解为三个新的矩阵,并广泛应用于当前许多的应用中,包括主成分分析(PCA)和推荐系统(RS)。
Simon Funk 在2006年的 Netflix 竞赛中提出并使用了一个非常好的策略,改方法将矩阵分解为两个权重矩阵,并使用梯度下降来找到特征和权重所对应的的最优值。实质上,这是不同于 SVD 方法的另一种技术,将其称为矩阵分解更为合适。
随着这两种方法的广泛应用,研究者并没有严谨地在术语上区分这两种方法,而是统一将其称为 SVD。
原文链接:
https://medium.freecodecamp.org/singular-value-decomposition-vs-matrix-factoring-in-recommender-systems-b1e99bc73599
(本文为AI科技大本营整理文章,转载请微信联系 1092722531)
◆
CTA核心技术及应用峰会
◆
5月25-27日,由中国IT社区CSDN与数字经济人才发展中心联合主办的第一届CTA核心技术及应用峰会将在杭州国际博览中心隆重召开,峰会将围绕人工智能领域,邀请技术领航者,与开发者共同探讨机器学习和知识图谱的前沿研究及应用。
更多重磅嘉宾请识别海报二维码查看,目前会议早鸟票发售中(原票价1099元),点击阅读原文即刻抢购。添加小助手微信15101014297,备注“CTA”,了解票务以及会务详情。

推荐阅读
他25岁进贝尔实验室,32岁提信息论,40岁办达特茅斯会议,晚年患上阿兹海默 | 人物志
硬核粉丝 | 清华双胞胎“YCY Dance Now”杀进超越杯编程大赛决赛
小样,加张图你就不认识我了?“补丁”模型骗你没商量!| 技术头条
东大漆桂林、清华李涓子、复旦肖仰华等大牛确认出席CTA峰会!5月一起打卡杭州
京东 60 天哗变!CTO 成优化第一人 | 畅言
异构计算=未来?一文带你秒懂3大主流异构
《互联网人叹气图鉴》
回报率29%! 大神用情感分析创建一个比特币交易算法, 原来交易玩的是心理战
她说:为啥程序员都特想要机械键盘?这答案我服!

相关文章:

[转]程序员技术练级攻略
2019独角兽企业重金招聘Python工程师标准>>> 月光博客6月12日发表了《写给新手程序员的一封信》,翻译自《An open letter to those who want to start programming》,我的朋友(他在本站的id是Mailper)告诉我࿰…

聊天机器人落地及进阶实战 | 公开课速记
嘉宾 | 邵浩编辑 | suiling来源 | AI科技大本营在线公开课近年来,聊天机器人技术及产品得到了快速的发展。聊天机器人作为人工智能技术的杀手级应用,发展得如火如荼,各种智能硬件层出不穷。本次公开课中,AI科技大本营联合电子工业…

【GStreamer】官网基本教程学习(basic-tutorial)
目录 下载和编译basic-tutorial-1.c 直接创建管道播放视频basic-tutorial-2.c 创建元件-->装入管道-->连接元件0、gstreamer 函数调用顺序1、元素 videotestsrc 的 pattern 属性详解2、GST_BIN 将其它类型指针转换成 GstBin*basic-tutorial-3.c 信号触发后再连接元件0、g…

IdentityServer4关于多客户端和API的最佳实践【含多类型客户端和API资源,以及客户端分组实践】【中】...
上一篇文章中,我们已经完成了服务端数据库的搭建,本篇主要处理多【传统HTTP】【依赖CORE环境】客户端之间协同在线【SSO】以及不需要SSO的场景处理。 目标: 1)实现多类型客户端接入IdentityServer 后文简称【IDSV】 2)…

WEB SSH Ajaxterm客户端配置(1)
Ajaxterm是一款基于Web的SSH客户端软件,它是采用Python编写的,这也就保证了它能在多种Linux发行版的系统中使用,同时它的安装非常简单。实验环境:Centos 5.5 ip:192.168.20.165pcre-7.8.tar.gzAjaxterm-0.10.tar.gzn…

如何为回归问题选择最合适的机器学习方法?
作者 | 何从庆本文经授权转载自 AI算法之心(id:AIHeartForYou)在目前的机器学习领域中,最常见的三种任务就是:回归分析、分类分析、聚类分析。在之前的文章中,我曾写过一篇《15分钟带你入门sklearn与机器学…

【Qt】获取本地IP(IPv4)
1、问题描述 获取本地IP列表有“127.0.0.1”、IPv4、IPv6等,一般使用IPv4,如何从已经获取的IP列表中挑出IPv4。 2、解决方法 QString ipv4; auto ips = QNetworkInterface::allAddresses(); foreach (auto ip, ipps) {if ( (ip.

2.2元组介绍+字符串操作
元组可以理解为“一旦创建就不能再修改的列表”,所以也叫只读列表 语法:names("A","B","C","D") 他只有两个方法: ①count ②index 字符串操作: 示例:name"chan" 1…

医生再添新助手!深度学习诊断传染病 | 完整代码+实操
作者 | Dipanjan (DJ) Sarkar译者 | Monanfei编辑 | Rachel、Jane出品 | AI科技大本营(id:rgznai100)【导读】文本基于深度学习和迁移学习方法,对疟疾等传染病检测问题进行了研究。作者对疟疾的检测原理以及迁移学习理论进行了介绍…

DIV限制宽度,字符断行,避免变形
代码如下:<div style"width:740px;word-break:break-all;word-wrap:break-word;">参考文章怎么强制限制div宽度转载于:https://www.cnblogs.com/leftfist/archive/2012/02/07/4258078.html

【渗透】node.js经典问题
1.循环问题 当循环调用 require() 时,一个模块可能在未完成执行时被返回。例如以下情况:a.js: exports.done false; const b require(./b.js); console.log(在 a 中,b.done %j, b.done); exports.done true; console.log(a 结束); b.js: console.log…

【Qt】Ubuntu下Qt应用程序自启动设置
1、问题描述 第一步,确保手动启动Qt程序没有报错!如果报以下错误,参见博客 qt.qpa.xcb: could not connect to display qt.qpa.plugin: Could not load the Qt platform plugin "xcb" in "" even though it was found. This application failed to s…

Tarjan算法应用 (割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)问题)...
转载自:http://hi.baidu.com/lydrainbowcat/blog/item/2194090a96bbed2db1351de8.html 基本概念: 1.割点:若删掉某点后,原连通图分裂为多个子图,则称该点为割点。 2.割点集合:在一个无向连通图中࿰…

【JavaScript】Ubuntu16.04安装vscode+npm+yarn
一、安装vscode vscode官网(https://code.visualstudio.com/)下载linux deb文件 下载deb后,使用dpkg -i 命令安装 sudo dpkg -i code_1.45.1-1589445302_amd64.deb在终端执行命令code来启动vscode 二、安装nodejs curl -sL https://deb…

C++大数加法
1 #include <iostream>2 #include<deque>3 #include<string>4 5 using namespace std;6 7 string add(string a, string b) //此函数默认a的长度大于b(可以在main函数里用if语句控制a的长度大于b)8 {9 deque<int>sum; //sum用来存储和的每…

重磅!Facebook更新PyTorch 1.1,打算跨GPU分割神经网络
时隔半年不到,PyTorch 已经从之前的 1.0 升级到 1.1 版本了。刚刚,Facebook 在年度开发者大会 F8 上宣布正式发布 PyTorch 1.1 版本,这是对 PyTorch 1.0 的一次大的功能升级。 作者 | 琥珀 出品 | AI科技大本营(ID:rgznai100&…

红旗Linux认证简介
红旗Linux认证 一、课程名称:红旗Linux认证产品专家(RAP) 课程简介: 主要针对初次使用红旗Linux desktop的学员而编制,注重实用性,是红旗Linux的一门入门课程。 采用的教材是《红旗Linux桌面应用教程》&…
【Git】git clone时下载速度太慢的解决方法(亲测有效)
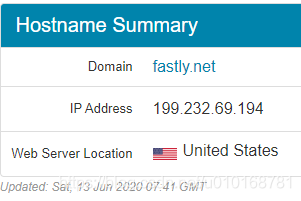
1、参考博客 https://www.jianshu.com/p/3f6477049ece2、原因 git clone特别慢是因为github.global.ssl.fastly.net域名被限制了。 只要找到这个域名对应的ip地址,然后在hosts文件中加上ip–>域名的映射,刷新DNS缓存便可。 3、解决方法 3.1 获取I…

JHipster技术简介
本文简单介绍Jhipster是什么,为什么用Jhipster,怎么用Jhipster。 WHAT - 技术栈 JHipster是什么 JHipster是一个开发平台,用于生成,开发,部署Spring Boot Angular/React Web Application和Spring microservices。 JHi…

如何确定最佳训练数据集规模?6 大必备“锦囊”全给你了
【导读】对于机器学习而言,获取数据的成本有时会非常昂贵,因此为模型选择一个合理的训练数据规模,对于机器学习是至关重要的。在本文中,作者针对线性回归模型和深度学习模型,分别介绍了确定训练数据集规模的方法。 作者…

Android实现左右滑动效果
本示例演示在Android中实现图片左右滑动效果。 关于滑动效果,在Android中用得比较多,本示例实现的滑动效果是使用ViewFlipper来实现的,当然也可以使用其它的View来实现。接下来就让我们开始实现这种效果。为了方便大家理解,我们先…

假如AI也会diss人类,他们会这样.....
1酷炫、未来感、强大、没灵气、不给力、垃圾、高深——如果有一个东西适用于以上所有这些词,那它一定是人工智能。人工智能的火爆一直伴随着争议和调侃。尤其是现在,大数据和机器学习已经融入到我们的生活,网上关于人工智障的吐槽却只增不减。…

[Go]在vscode中添加对模板文件tmpl的html语法自动补全的支持
1、打开设置界面 依次点击:“文件” --> “首选项” --> “设置” 2、打开文件配置 依次点击:“文本编辑器” --> “文件” --> “在settings.json中编辑” 3、添加对tmpl后缀文件的html语法自动补全支持 4、效果 html关键字高亮显示…

Docker 宿主机定时清除容器的运行日志
为什么80%的码农都做不了架构师?>>> docker 宿主机定时清除容器的运行日志 一般docker容器都是最小化安装,不仅如此系统定时器相关的服务也不存在,自己去安装也很麻烦,故此直接使用宿主机的定时器即可。 一、在容器中…

企业数据库合规的最佳实践
PCI DSS当前对于数据库要求有下述明确的控制措施: • 对访问任意数据库的所有用户进行认证。 • 所有用户访问任何数据库时,用户的查询和操作(例如移动、拷贝和删除)只能通过编程性事务(例如存储过程)。 •…

Docker网络解决方案-Flannel部署记录
Docker跨主机容器间网络通信实现的工具有Pipework、Flannel、Weave、Open vSwitch(虚拟交换机)、Calico实现跨主机容器间的通信。其中Pipework、Weave、Flannel,三者的区别是: Weave的思路 12在每个宿主机上布置一个特殊的route的…

【FFmpeg】警告:[hls] pkt.duration = 0, maybe the hls segment duration will not precise
1、问题描述 在使用ffmpeg编程生成m3u8文件时,报警告 [hls @ 0x7f26b4181840] pkt->duration = 0, maybe the hls segment duration will not precise2、原因分析 根据警告提示信息, AVPacket.duration的值设为了0,可能会导致hls在分段时时间不精确。 根据警告信息搜索…

反转字符串/列表、改变递归次数限制、else用法...Python 冷知识(四)
本文转载自Python编程时光(ID:Python-Time)冷知识系列,已经更新至第四篇。前三篇传送门在此,还没阅读的可以学习一下。谈谈 Python 那些不为人知的冷知识(一)谈谈 Python 那些不为人知的冷知识(…

我学Delphi心得与笔记-------在控件上如何禁用Ctrl+V
项目中用到一个TJamShellList组件,此组件实现绑定查询图片,发现在使用CtrlC的同时也可以使用CtrlV结果将一个图处复制了多份,这样就不行了:( 于是,想了一个办法,禁用了CtrlV组合按键,代码如下: //在KeyDown事件中写如下…

15分钟带你入门sklearn与机器学习——分类算法篇
作者 | 何从庆本文转载自AI算法之心(ID:AIHeartForYou)【导读】众所周知,Scikit-learn(以前称为scikits.learn)是一个用于Python编程语言的免费软件机器学习库。它具有各种分类,回归和聚类算法,…
