当前位置：首页 > 编程日记 > 正文

吴恩达团队：神经网络如何正确初始化？

编程日记 2025-01-04 14:00:00

640?wx_fmt=jpeg

来源 | deeplearning.ai

编译 | 刘静

转载自图灵TOPIA(ID:turingtopia)

初始化对训练深度神经网络的收敛性有重要影响。简单的初始化方案可以加速训练，但是它们需要小心避免常见的陷阱。

近期，deeplearning.ai就如何有效地初始化神经网络参数发表了交互式文章，图灵君将结合这篇文章与您一起探索以下问题：

1、有效初始化的重要性

2、梯度爆炸或消失的问题

3、什么是正确的初始化？

4、Xavier初始化的数学证明

一、有效初始化的重要性

要构建机器学习算法，通常需要定义一个体系结构（例如Logistic回归，支持向量机，神经网络）并训练它来学习参数。以下是神经网络的常见训练过程：

1、初始化参数

2、选择优化算法

3、重复这些步骤：

a、正向传播输入

b、计算成本函数

c、使用反向传播计算与参数相关的成本梯度

d、根据优化算法，使用梯度更新每个参数

然后，给定一个新的数据点，您可以使用该模型来预测它的类。

初始化步骤对于模型的最终性能至关重要，它需要正确的方法。为了说明这一点，请考虑下面的三层神经网络。您可以尝试使用不同的方法初始化此网络，并观察它对学习的影响。

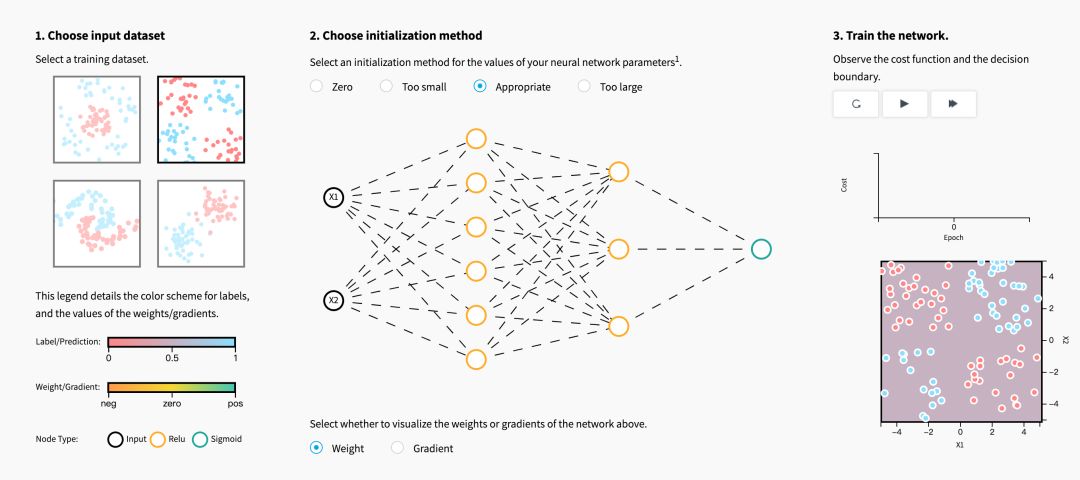
640?wx_fmt=png

（网址：https://www.deeplearning.ai/ai-notes/initialization/）

感兴趣的同学可直接登陆、操作体验。

当初始化方法为零时，对于梯度和权重，您注意到了什么?

用零初始化所有权重会导致神经元在训练期间学习相同的特征。

实际上，任何常量初始化方案的性能表现都非常糟糕。考虑一个具有两个隐藏单元的神经网络，并假设我们将所有偏差初始化为0，并将权重初始化为一些常数α。如果我们在该网络中正向传播输入（x1，x2），则两个隐藏单元的输出将为relu（αx1+αx2）。因此，两个隐藏单元将对成本具有相同的影响，这将导致相同的梯度。

因此，两个神经元将在整个训练过程中对称地进化，有效地阻止了不同的神经元学习不同的东西。

在初始化权重时，如果值太小或太大，关于成本图，您注意到了什么?

尽管打破了对称性，但是用值（i）太小或（ii）太大来初始化权重分别导致（i）学习缓慢或（ii）发散。

为高效训练选择适当的初始化值是必要的。 我们将在下一节进一步研究。

二、梯度的爆炸或消失问题

考虑这个9层神经网络。

640?wx_fmt=png

在优化循环的每次迭代（前向，成本，后向，更新）中，我们观察到当您从输出层向输入层移动时，反向传播的梯度要么被放大，要么被最小化。如果您考虑以下示例，此结果是有意义的。

假设所有激活函数都是线性的（标识函数）。然后输出激活是：

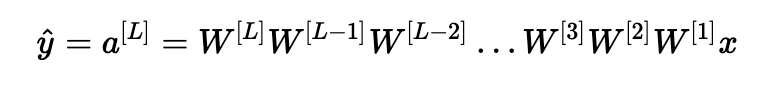
640?wx_fmt=png

其中，L=10,W[1],W[2],…,W[L−1] 都是大小为(2,2)的矩阵，因为层[1]到[L-1]有2个神经元，接收2个输入。考虑到这一点，为了便于说明，如果我们假设W[1]=W[2]=⋯=W[L−1]=W，输出预测是y^=W[L]WL−1x （其中 WL−1 将矩阵 W取为L-1的幂，而W[L] 表示Lth矩阵）。

初始化值太小，太大或不合适的结果是什么？

情形1：过大的初始化值会导致梯度爆炸

考虑这样一种情况:初始化的每个权重值都略大于单位矩阵。

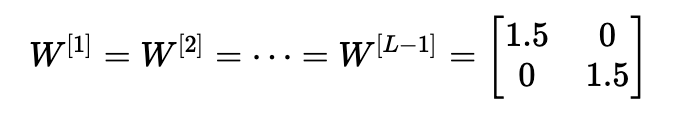
640?wx_fmt=png

这简化为y^=W[L]1.5L−1x，并且a[l] 的值随l呈指数增加。当这些激活用于反向传播时，就会导致梯度爆炸问题。也就是说，与参数相关的成本梯度太大。这导致成本围绕其最小值振荡。

情形2：初始化值太小会导致梯度消失

类似地，考虑这样一种情况:初始化的每个权重值都略小于单位矩阵。

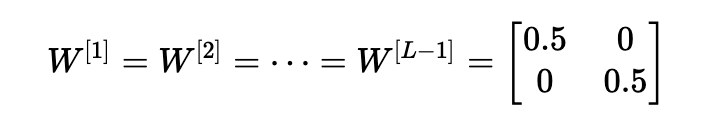
640?wx_fmt=png

这简化为 y^=W[L]0.5L−1x，并且激活a [l]的值随l呈指数下降。当这些激活用于反向传播时，这会导致消失的梯度问题。相对于参数的成本梯度太小，导致在成本达到最小值之前收敛。

总而言之，使用不适当的值初始化权重将导致神经网络训练的发散或减慢。 虽然我们用简单的对称权重矩阵说明了梯度爆炸/消失问题，但观察结果可以推广到任何太小或太大的初始化值。

三、如何找到合适的初始化值

为了防止网络激活的梯度消失或爆炸，我们将坚持以下经验法则：

1、激活的平均值应为零。

2、激活的方差应该在每一层保持不变。

在这两个假设下，反向传播的梯度信号不应该在任何层中乘以太小或太大的值。它应该移动到输入层而不会爆炸或消失。

更具体地考虑层l，它的前向传播是：

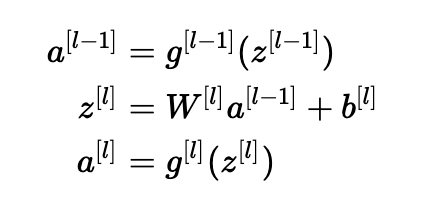
640?wx_fmt=png

我们希望以下内容：

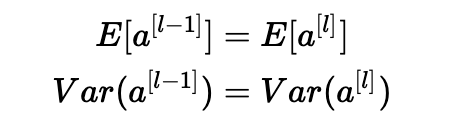
640?wx_fmt=png

确保零均值并保持每层输入方差的值不会产生爆炸/消失信号，我们稍后会解释。该方法既适用于前向传播（用于激活），也适用于反向传播传播（用于激活成本的梯度）。推荐的初始化是Xavier初始化（或其派生方法之一），对于每个层l：

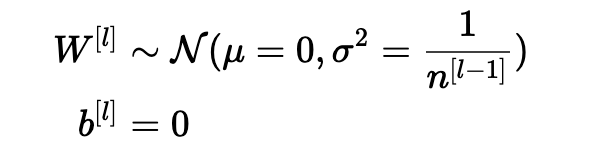
640?wx_fmt=png

换句话说，层l的所有权重是从正态分布中随机选取的，其中均值μ= 0且方差σ2= n [l-1] 1其中n [l-1]是层l-1中的神经元数。偏差用零初始化。

下面的可视化说明了Xavier初始化对五层全连接神经网络的每个层激活的影响。

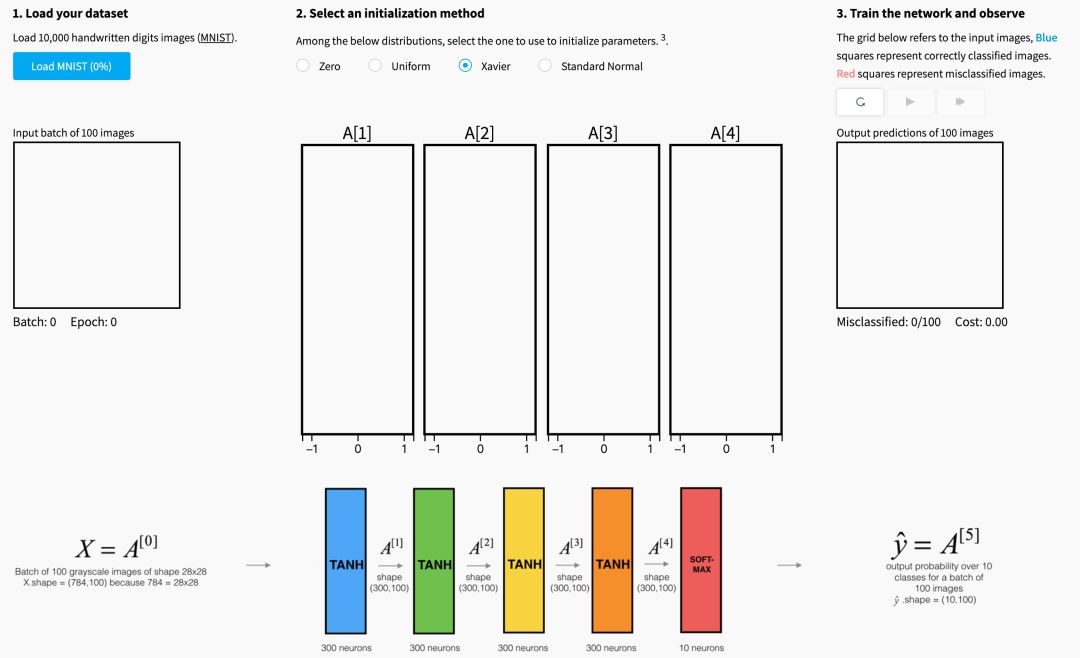
640?wx_fmt=png

您可以在Glorot等人中找到这种可视化背后的理论。（2010年）。下一节将介绍Xavier初始化的数学证明，并更准确地解释为什么它是一个有效的初始化。

四、Xavier初始化的合理性

在本节中，我们将展示Xavier初始化使每个层的方差保持不变。我们假设层的激活是正态分布在0附近。有时候，理解数学原理有助于理解概念，但不需要数学，就可以理解基本思想。

让我们对第（III）部分中描述的层l进行处理，并假设激活函数为tanh。前向传播是：

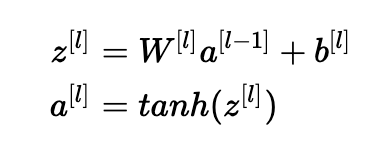
640?wx_fmt=png

目标是导出Var（a [l-1]）和Var（a [l]）之间的关系。然后我们将理解如何初始化我们的权重，使得： Var(a[l−1])=Var(a[l])。

假设我们使用适当的值初始化我们的网络，并且输入被标准化。在训练初期，我们处于tanh的线性状态。值足够小，因此tanh(z[l])≈z[l]，意思是：

640?wx_fmt=png

此外，z[l]=W[l]a[l−1]+b[l]=向量(z1[l],z2[l],…,zn[l][l])其中 zk[l]=∑j=1n[l−1]wkj[l]aj[l−1]+bk[l]。为简单起见，我们假设b[l]=0 （考虑到我们将选择的初始化选择，它将最终为真）。因此，在前面的方程Var(a[l−1])=Var(a[l]) 中逐个元素地看，现在给出：

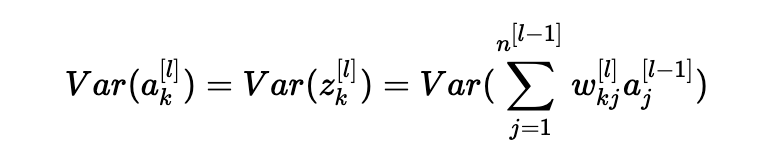
640?wx_fmt=png

常见的数学技巧是在方差之外提取求和。为此，我们必须做出以下三个假设：

1、权重是独立的，分布相同；

2、输入是独立的，分布相同；

3、权重和输入是相互独立的。

因此，现在我们有：

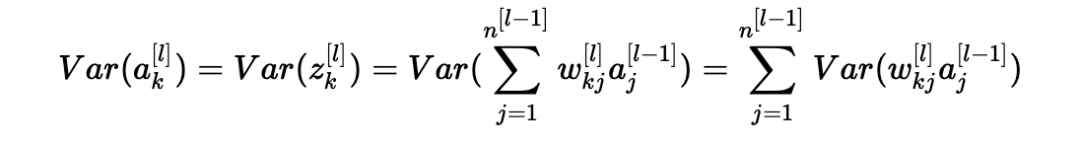
640?wx_fmt=png

另一个常见的数学技巧是将乘积的方差转化为方差的乘积。公式如下:

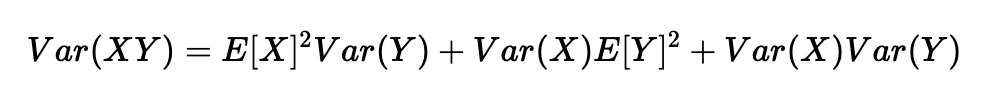
640?wx_fmt=png

使用X=wkj[l]和Y=aj[l−1]的公式，我们得到：

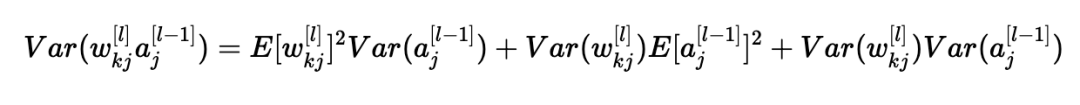
640?wx_fmt=png

我们差不多完成了！第一个假设导致E[wkj[l]]2=0，第二个假设导致E[aj[l−1]]2=0，因为权重用零均值初始化，输入被归一化。从而：

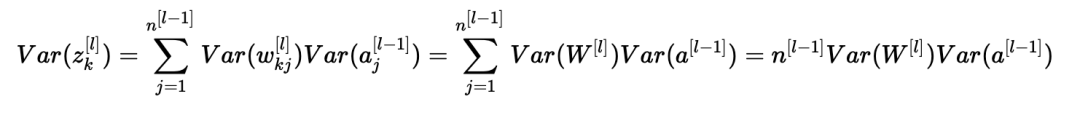
640?wx_fmt=png

上述等式源于我们的第一个假设，即:

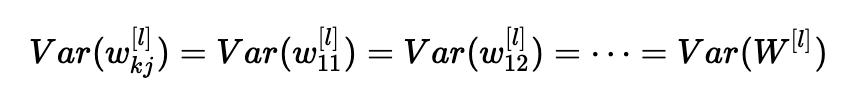
640?wx_fmt=png

同样，第二个假设导致：

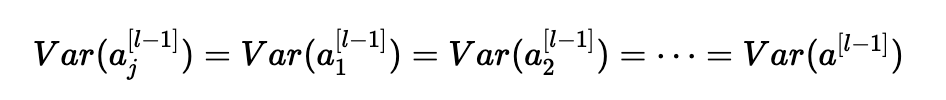
640?wx_fmt=png

同样的想法：

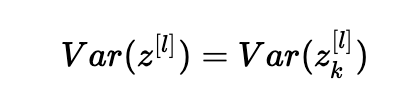
640?wx_fmt=png

总结一下，我们有:

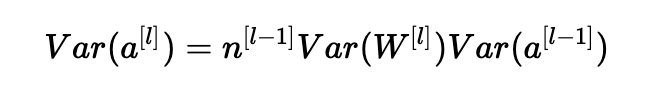
640?wx_fmt=png

瞧！如果我们希望方差在各层之间保持不变(Var(a[l])=Var(a[l−1]))，我们需要Var(W[l])=n[l−1]1。这证明了Xavier初始化的方差选择是正确的。

请注意，在前面的步骤中，我们没有选择特定的层ll。因此，我们已经证明这个表达式适用于我们网络的每一层。让LL成为我们网络的输出层。在每一层使用此表达式，我们可以将输出层的方差链接到输入层的方差：

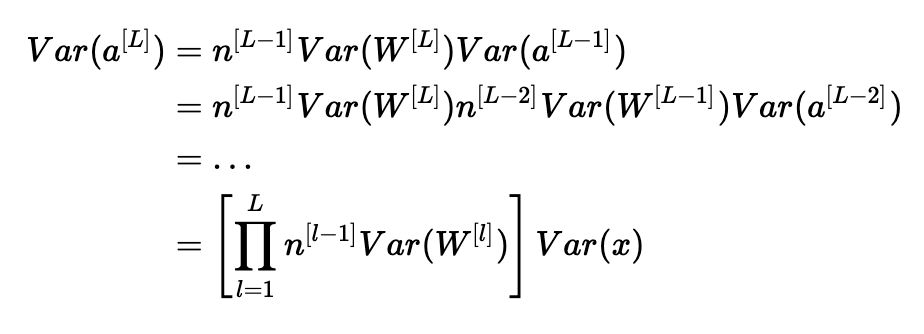
640?wx_fmt=png

根据我们如何初始化权重，我们的输出和输入的方差之间的关系会有很大的不同。请注意以下三种情况。

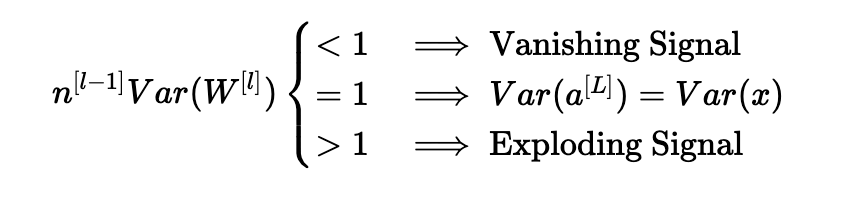
640?wx_fmt=png

因此，为了避免正向传播信号的消失或爆炸，我们必须通过初始化Var(W[l])=n[l−1]1来设置n[l−1]Var(W[l])=1。

在整个证明过程中，我们一直在处理在正向传播期间计算的激活。对于反向传播的梯度也可以得到相同的结果。这样做，您将看到，为了避免梯度消失或爆炸问题，我们必须通过初始化 Var(W[l])=n[l]1来设置n[l]Var(W[l])=1。

结论

实际上，使用Xavier初始化的机器学习工程师会将权重初始化为N(0,n[l−1]1) 或N(0,n[l−1]+n[l]2)。后一分布的方差项是n [l-1] 1和n [1] 1的调和平均值。

这是Xavier初始化的理论依据。 Xavier初始化与tanh激活一起工作。还有许多其他初始化方法。例如，如果您正在使用ReLU，则通常的初始化是He初始化（He et al，Delving Deep into Rectifiers），其中权重的初始化方法是将Xavier初始化的方差乘以2。虽然这种初始化的理由稍微复杂一些，但它遵循与tanh相同的思考过程。

参考链接：

https://www.deeplearning.ai/ai-notes/initialization/

（*本文为 AI科技大本营转载文章，转载请联系原作者）

◆

CTA核心技术及应用峰会

◆

5月25-27日，由中国IT社区CSDN与数字经济人才发展中心联合主办的第一届CTA核心技术及应用峰会将在杭州国际博览中心隆重召开，峰会将围绕人工智能领域，邀请技术领航者，与开发者共同探讨机器学习和知识图谱的前沿研究及应用。

更多重磅嘉宾请识别海报二维码查看。目前会议8折预售票抢购中，点击阅读原文即刻抢购。添加小助手微信15101014297，备注“CTA”，了解票务以及会务详情。

640?wx_fmt=jpeg

推荐阅读

赌5毛钱，你解不出这道Google面试题
@程序员，别再自己闷头学了
我用Python，3分钟快速实现，9种经典排序算法的可视化
手把手教你利用爬虫爬网页（Python代码）
云在物联网中的惊人优势 | 技术头条
天才少年，大学创业，29 岁创立 Coinbase！| 人物志
没上过大学，曾拒绝盖茨的 Offer，四代码农靠他吃饭 | 人物志
狂赚320亿! 小伙建立第一个区块链国家, 国土面积7km², 自由之城诞生记
小姐姐公开征婚高智商 IT 男：微信号竟要质数解密？

640?wx_fmt=png

https://www.dkcj.cn/info/34820.html

吴恩达团队：神经网络如何正确初始化？

相关文章：

【Qt】Qt再学习（三）：Chart Themes Example（常用图表）

eyoucms range 范围判断标签

现实迷途第七章特殊客户

BZOJ1396:识别子串(SAM)

【Qt】Qt再学习（四）：Editable Tree Model Example

千亿级照片，毫秒间匹配最佳结果，微软开源Bing搜索背后的关键算法

【Qt】Qt再学习（五）：HTTP Example（HTTP下载文件的示例）

面对互联网一线大厂，这些技术你需要了解！

Android定制：修改开机启动画面

盛大游戏卷入“沙巴克”商标之争

iOS开发经验总结

焦虑的 BAT、不安的编程语言，揭秘程序员技术圈生存现状！

【Qt】Qt再学习（六）：Qt中JSON保存和加载的示例

H3C ER3260通过Console口重装软件修复路由器

【Qt】Qt再学习（七）：QLocalServer、QLocalSocket

百度宣布：搜索业务总裁向海龙离职，另回购10亿美元股份

Oracle SQL高级编程——分析函数（窗口函数）全面讲解

学习html5系列之比较典型的div滥用

【Qt】Qt再学习（八）：Media Player（Qt实现多媒体播放器）

一次改变未来10年人生的机会

SQL Server 2008之WaitFor

“搞垮” 微博服务器？每天上亿条用户推送是如何做到的

【Qt】Qt再学习（九）：并发 QtConcurrent、QFuture、QFutureWatcher

Git——如何将本地项目提交至远程仓库(第一次)

连接不上ftp解决方案

Python3破冰人工智能，你需要掌握一些数学方法

【Qt】QtCreator无法调试终端程序，启动报错SIGSTOP

Centos7 下配置 rsync 以及 rsync+inotify 实时同步

网站排名下降的原因

@程序员，Python 3还有哪些未Get的潜藏技能？| 技术头条