那些年,让我面试头大的几个排序算法,今天终于搞懂了!

作者 | 逆流的鱼yuiop
转载自何俊林(ID:smartyuge)
算法上,最基础的就是排序算法,几乎在面试中,或多或少会要求你手写一些基础算法。今天鱼哥带大家这些基础算法回顾下。
快速排序
介绍:
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]和A[i]的值交换;
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]的值交换;
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
代码:
//快速排序
private void quickSort(int[] a ,int left,int right) {
if(left < right){
int i,j,t,temp;
temp=a[left]; //temp中存的就是基准数
i=left;
j=right;
while(i!=j)
{
//顺序很重要,要先从右边开始找
while(a[j]>=temp && i<j)
j--;
//再找右边的
while(a[i]<=temp && i<j)
i++;
//交换两个数在数组中的位置
if(i<j)
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
}
//最终将基准数归位
a[left]=a[i];
a[i]=temp;
quickSort(a,left,i-1);//继续处理左边的,这里是一个递归的过程
quickSort(a,i+1,right);//继续处理右边的 ,这里是一个递归的过程
}
}
// 调用
quickSort(a,0,a.length-1);
归并排序
介绍:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
步骤:
1、申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2、设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4、重复步骤3直到某一指针达到序列尾;
5、将另一序列剩下的所有元素直接复制到合并序列尾。
代码:
public class MergeSort {
// private static long sum = 0;
/**
* * <pre>
* * 二路归并
* * 原理:将两个有序表合并和一个有序表
* * </pre>
* *
* * @param a
* * @param s
* * 第一个有序表的起始下标
* * @param m
* * 第二个有序表的起始下标
* * @param t
* * 第二个有序表的结束下标
* *
*/
private static void merge(int[] a, int s, int m, int t) {
int[] tmp = new int[t - s + 1];
int i = s, j = m, k = 0;
while (i < m && j <= t) {
if (a[i] <= a[j]) {
tmp[k] = a[i];
k++;
i++;
} else {
tmp[k] = a[j];
j++;
k++;
}
}
while (i < m) {
tmp[k] = a[i];
i++;
k++;
}
while (j <= t) {
tmp[k] = a[j];
j++;
k++;
}
System.arraycopy(tmp, 0, a, s, tmp.length);
}
/**
* *
* * 每次归并的有序集合的长度
*/
public static void mergeSort(int[] a, int s, int len) {
int size = a.length;
int mid = size / (len << 1);
int c = size & ((len << 1) - 1);
// -------归并到只剩一个有序集合的时候结束算法-------//
if (mid == 0)
return;
// ------进行一趟归并排序-------//
for (int i = 0; i < mid; ++i) {
s = i * 2 * len;
merge(a, s, s + len, (len << 1) + s - 1);
}
// -------将剩下的数和倒数一个有序集合归并-------//
if (c != 0)
merge(a, size - c - 2 * len, size - c, size - 1);
// -------递归执行下一趟归并排序------//
mergeSort(a, 0, 2 * len);
}
public static void main(String[] args) {
int[] a = new int[]{4, 3, 6, 1, 2, 5};
mergeSort(a, 0, 1);
for (int i = 0; i < a.length; ++i) {
System.out.print(a[i] + " ");
}
}
}
堆排序
介绍:
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
步骤:
推荐看这篇文:https://www.cnblogs.com/chengxiao/p/6129630.html
代码:
建立大根堆的方法:
//构建大根堆:将array看成完全二叉树的顺序存储结构
private int[] buildMaxHeap(int[] array){
//从最后一个节点array.length-1的父节点(array.length-1-1)/2开始,直到根节点0,反复调整堆
for(int i=(array.length-2)/2;i>=0;i--){
adjustDownToUp(array, i,array.length);
}
return array;
}
//将元素array[k]自下往上逐步调整树形结构
private void adjustDownToUp(int[] array,int k,int length){
int temp = array[k];
for(int i=2*k+1; i<length-1; i=2*i+1){ //i为初始化为节点k的左孩子,沿节点较大的子节点向下调整
if(i<length && array[i]<array[i+1]){ //取节点较大的子节点的下标
i++; //如果节点的右孩子>左孩子,则取右孩子节点的下标
}
if(temp>=array[i]){ //根节点 >=左右子女中关键字较大者,调整结束
break;
}else{ //根节点 <左右子女中关键字较大者
array[k] = array[i]; //将左右子结点中较大值array[i]调整到双亲节点上
k = i; //【关键】修改k值,以便继续向下调整
}
}
array[k] = temp; //被调整的结点的值放人最终位置
}
排序
//堆排序
public int[] heapSort(int[] array){
array = buildMaxHeap(array); //初始建堆,array[0]为第一趟值最大的元素
for(int i=array.length-1;i>1;i--){
int temp = array[0]; //将堆顶元素和堆低元素交换,即得到当前最大元素正确的排序位置
array[0] = array[i];
array[i] = temp;
adjustDownToUp(array, 0,i); //整理,将剩余的元素整理成堆
}
return array;
}
删除堆顶元素(即序列中的最大值):先将堆的最后一个元素与堆顶元素交换,由于此时堆的性质被破坏,需对此时的根节点进行向下调整操作。
//删除堆顶元素操作
public int[] deleteMax(int[] array){
//将堆的最后一个元素与堆顶元素交换,堆底元素值设为-99999
array[0] = array[array.length-1];
array[array.length-1] = -99999;
//对此时的根节点进行向下调整
adjustDownToUp(array, 0, array.length);
return array;
}
对堆的插入操作:先将新节点放在堆的末端,再对这个新节点执行向上调整操作。
假设数组的最后一个元素array[array.length-1]为空,新插入的结点初始时放置在此处。
//插入操作:向大根堆array中插入数据data
public int[] insertData(int[] array, int data){
array[array.length-1] = data; //将新节点放在堆的末端
int k = array.length-1; //需要调整的节点
int parent = (k-1)/2; //双亲节点
while(parent >=0 && data>array[parent]){
array[k] = array[parent]; //双亲节点下调
k = parent;
if(parent != 0){
parent = (parent-1)/2; //继续向上比较
}else{ //根节点已调整完毕,跳出循环
break;
}
}
array[k] = data; //将插入的结点放到正确的位置
return array;
}
选择排序
介绍:
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方式样。
排序效果:
代码:
public static void selectSort(int[] a) {
if((a == null) || (a.length == 0))
return ;
for(int i = 0;i < a.length - 1;i ++){
int minIndex = i; // 无序区的最小数据数组下标
for(int j = i + 1;j < a.length;j ++){
// 在无序区中找到最小数据并保存其数组下标
if(a[j] < a[minIndex]){
minIndex = j;
}
}
// 将最小元素放到本次循环的前端
int temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
冒泡排序
介绍:
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
步骤:
1、比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2、对每一对相邻元素作同样操作,从开始第一对到结尾的最后一对。在这一点,最后的元素会是最大的数。
3、针对所有的元素重复以上的步骤,除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码:
public static void bubbleSort(int []arr) {
int[] arr = {12,23,34,56,56,56,78};
for(int i =0;i<arr.length-1;i++) {
for(int j=0;j<arr.length-i-1;j++) {//-1为了防止溢出
if(arr[j]>arr[j+1]) {
int temp = arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
排序效果:
插入排序
介绍:
插入排序(Insertion sort)是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分:第一部分包含了这个数组的所有元素,但将最后一个元素除外(让数组多一个空间才有插入的位置),而第二部分就只包含这一个元素(即待插入元素)。在第一部分排序完成后,再将这个最后元素插入到已排好序的第一部分中.
步骤:
1、从第一个元素开始,该元素可以认为已经被排序;
2、取出下一个元素,在已经排序的元素序列中从后向前扫描;
3、如果该元素(已排序)大于新元素,将该元素移到下一位置;
4、重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
5、将新元素插入到该位置中,重复步骤2。
排序代码:
//直接插入
private void InsertSort(int[] a) {
//直接插入排序
for (int i = 1; i < a.length; i++) {
//待插入元素
int temp = a[i];
int j;
for (j = i - 1; j >= 0; j--) {
//将大于temp的往后移动一位
if (a[j] > temp) {
a[j + 1] = a[j];
} else {
break;
}
}
a[j + 1] = temp;//插入进来
}
}
希尔排序
介绍:
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。 [1]
步骤:
可以这篇博客,图解版,非常详细:
http://www.cnblogs.com/chengxiao/p/6104371.html
代码:
public static void main(String [] args)
{
int[] a = {49,38,65,97,76,13,27,49,78,34,12,64,1};
//希尔排序
int d=a.length;
while(true)
{
d=d/2;
for(int x=0;x<d;x++)
{
for(int i=x+d;i<a.length;i=i+d)
{
int temp=a[i];
int j;
for(j=i-d;j>=0&&a[j]>temp;j=j-d)
{
a[j+d]=a[j];
}
a[j+d]=temp;
}
}
if(d==1)
{
break;
}
}
System.out.println("排序之后:");
for(int i=0;i<a.length;i++)
{
System.out.print(a[i]+" ");
}
}
(*本文为 AI科技大本营转载文章,转载请联系原作者)
◆
CTA核心技术及应用峰会
◆
5月25-27日,由中国IT社区CSDN与数字经济人才发展中心联合主办的第一届CTA核心技术及应用峰会将在杭州国际博览中心隆重召开,峰会将围绕人工智能领域,邀请技术领航者,与开发者共同探讨机器学习和知识图谱的前沿研究及应用。议程设置请请识别海报二维码查看。
目前CTA峰会倒计时5天!还没有拿到入场券的小伙伴可以扫描识别海报二维码或者点击阅读原文,即刻抢购。你也添加小助手微信15101014297,备注“CTA”,了解票务以及会务详情。

推荐阅读
掌声送给TensorFlow 2.0!用Keras搭建一个CNN | 入门教程
一文回顾AI绘画的成长之路:从简笔画到真实人脸生成
清华AI学堂班:姚期智担任首席教授,2019年首批招收30人
中国AI开发者真实现状:写代码这条路,会走多久?
520 这天,我突然意识到,她根本配不上我这么聪明的男人
厉害!女学生偷师男子学校,变身区块链开发工程师
确实, 5G与物联网离不开区块链!
刷了一个半月算法题,我薪资终于Double了
Linux 之父:我就是觉得苹果没意思!| 人物志
这本京东断货王的Python神书,刷爆整个编程圈!

相关文章:

【天线】天线基础:名词解释
1、定向天线和全向天线 先上图,第一张图是定向天线(一根棍子加一块板),第二张图是全向天线(一根棍子) 网上的几种解释: 全向天线就是一个棍子,围绕棍子有一圈儿信号;定…

springBean生命周期----来自spring实战总结
1、Spring对bean进行实例化 2、Spring将值和bean的引用注入到bean对应的属性中(比如说注入到被依赖的bean的方法中或属性里) 3、如果bean实现了BeanNameAware接口,将会将bean的Id传入setBeanName()方法中 4、如果bean实现了BeanFactoryAware接口,将会设置bean的BeanFactory的引…

disk boot failure,insert system disk and press enter
每次一开机就出现提示:"disk boot failure,insert system disk and press enter"http://topic.csdn.net/t/20061202/08/5201096.html 转载于:https://blog.51cto.com/yfb880106/857829

深度讲解:web前端性能优化
一、课程简介: 1、课程大纲 涉及到的分类 网络层面构建层面浏览器渲染层面服务端层面涉及到的功能点 资源的合并与压缩图片编解码原理和类型选择浏览器渲染机制懒加载预加载浏览器存储缓存机制PWAVue-SSR前端性能优化原理 作用及原理如何与真实业务场景结合理论结合…

Google Android向华为“闭源”,华为手机迎来至暗时刻!
作者 | 屠敏转载自CSDN(ID:CSDNnews)居安思危任正非,未雨绸缪如华为。在贸易战的背景下,即使早在多年前已在多个层面做好“备胎”计划的华为,在面对美国对芯片乃至操作系统等系列釜底抽薪的打压时ÿ…

【C++】C++好书推荐
一、吴咏炜推荐 1、入门级 Bjarne Stroustrup, A Tour of C, 2nd ed. Addison-Wesley, 2018 中文版: 王刚译,《C 语言导学》(第二版)。机械工业出版社,2019 Bjarne Stroustrup, The C Programming Language, 4th ed. Addison-W…

HDOJ2569 ( 彼岸 ) 【递推公式】
f13f29f321f451猜测f(n)2*f(n-1)f(n-2)在纸上打草稿写出f3的情况,然后推出f4的情况(在f3后边加*2或*3就成)f3 f4 f3 f4 f3 f4111*3 222*3 333*3112*2 221*2 331*2113*2 223*2 332*2121*2 212*2 313*2131*2 …

【C++】new和malloc的区别
一、显而易见的区别 1、属性 new/delete是C关键字,需要编译器支持; malloc/free是库函数,需要头文件支持。 2、参数 使用new操作符申请内存分配时,无须指定内存块的大小,编译器会根据类型信息自行计算;…

消息队列的面试题7
1、面试题 如果让你写一个消息队列,该如何进行架构设计啊?说一下你的思路 2、面试官心里分析 其实聊到这个问题,一般面试官要考察两块: (1)你有没有对某一个消息队列做过较为深入的原理的了解,或…

《使女的故事》大火,AI是背后最大推手?
作者 | Just、Rachel出品 | AI科技大本营(ID:rgznai100)还记得大火的美剧《使女的故事》吗?先别着急回答,这次我们不讲剧情,而要说的是这部剧背后的发行方是美国 Hulu 网站。该网站是美国第二大付费在线视频平台&#…

jQuery事件处理一瞥
以前部门一直都是使用一个名为QTT的JS框架。最近老大提出要转用jQuery框架,需要将旧框架的一些JQ没有实现的功能移植到JQ中去。当我移植到event库的时候,以下是其代码: QTT.event {KEYS : {BACKSPACE : 8,TAB : 9,RETURN : 13,ESC : 27,SPAC…

【C++】零散知识
1、抛异常时,还会执行析构操作吗? 发生异常(抛异常)时,在该作用域中的局部非PAD变量(即,有构造函数和析构函数的变量)会执行析构操作。 2、new出的内存一定在堆上吗? …

百度景鲲“升职记”
整理 | 琥珀出品 | AI科技大本营(id:rgznai100)近日,据多家媒体报道,百度人力资源负责人崔珊珊发出晋升邮件宣布,智能生活事业群总经理景鲲晋升为副总裁。百度在晋升邮件中评价他:“敢打硬仗、能…

南通市公积金信息系统goldengate复制软件采购
(二)容灾软件部分:2套Oracle GoldenGate 11G ,1 CPU(必须提供原厂商针对本项目授权、质保承诺)。特性指标系统平台支持1. 支持主流操作系统,包括:IBM AIX、HP-UX、Linux、Sun Solaris、Mic…

开源需自立!Android、GitHub、Apache全线告急!
作者 | 胡巍巍&伍杏玲责编 | 唐小引出品 | CSDN(ID:CSDNnews)华为四面楚歌,“破窗效应”爆发!继5月16日美国商务部工业与安全局(BIS)将华为列入“实体清单”之后,越来越多的美国…

【C】linux下切换工作目录至程序所在目录
1、获取当前程序的绝对路径 /proc/self/exe是一个符号链接,代表当前程序的绝对路径 用readlink读取/proc/self/exe可以获取当前程序的绝对路径 2、从字符串中获取目录 char dirname(char path); 3、改变当前工作目录 int chdir(const char *path ); 4、完整示…
Eclipse基金会发布Eclipse Photon IDE
Eclipse基金会发布了最新版本的Eclipse IDE。Eclipse Photon带来对Java 10和Java EE 8的支持,增强了PHP开发工具和Dark主题等功能。\\Eclipse Java开发工具(Eclipse Java Development Tools,JDT)对Java 10提供了完整的支持&#x…

【C++】智能指针(一)入门
1、 智能指针背后的设计思想 智能指针背后的思想是RAII,参见博客【C】零散知识 我们先来看一个简单的例子: void remodel(std::string & str) {std::string * ptr new std::string(str);...if (weird_thing())throw exception();str *ptr; dele…

Oracle 11g Release 1 (11.1) PL/SQL_多维 Collection 类型和其异常
本文内容 多维 Collection Collection 异常 多维 Collection 虽然 collection 只有一维的,但可以模型一个多维的。创建一个 collection,其每个元素也是 collection 。例如,创建一个 varray 的 nested table,一个 varray 的 varray…

入门系列之使用fail2ban防御SSH服务器的暴力破解攻击
欢迎大家前往腾讯云社区,获取更多腾讯海量技术实践干货哦~ 本文由SQL GM 发表于云社区专栏 介绍 对于SSH服务的常见的攻击就是暴力破解攻击——远程攻击者通过不同的密码来无限次地进行登录尝试。当然SSH可以设置使用非密码验证验证方式来对抗这种攻击,例…

谁能解答我对知识图谱的上百个疑问?
近日,我们采访了东南大学认知智能研究所所长漆桂林教授和复旦大学知识工场实验室负责人肖仰华教授,围绕知识图谱这两年在研究与产业应用道路上的一些进展与仍面临的问题。漆桂林教授提到,近两年,知识图谱的研究在四大关键技术上都…

ecshop 商品颜色尺寸仿淘宝选择功能教程(2.7.0版本)
牵涉到的修改文件(default模板为例) /themes/default/style.css /themes/default/goods.dwt 注:此路径待修改模板路径.修改步骤:一:控制样式 1.打开/themes/ecshop/p_w_picpaths 加添图片test.gif. 2.打开/themes/ecshop/style.css 最下面添加: /*--------------颜色选择器CSS添…

【C++】Effective STL:50条有效使用STL的经验
第一条:慎重选择容器类型 1、C容器:先混个眼熟 序列容器:array、vector、string、deque、list、forward_list 有序关联容器:set、map、multiset、multimap 无序关联容器:unordered_set、unordered_map、unordered_mu…

ICML 2019接受论文:清华、北大领跑,谷歌强压枝头,BAT略显“低调”
整理 | 刘畅责编 | Jane、Rachel出品 | AI科技大本营(id:rgznai100)【AI科技大本营导语】今年 6 月,机器学习领域顶会 ICML 2019 将在美国举行。为了帮助大家更好了解会议论文的情况,博世(Bosch)…

C++STL 优先队列priority_queue使用
头文件:#include <queue> 一.申明方式 std::priority_queue<T> q; std::priority_queue<T, std::vector<T>, cmp> q;1.普通方法: priority_queue<int> q; //大的优先级高 priority_queue<int,vector<int>, …

【SVN】linux下svn命令参数详解(二)
svn全部子命令详解1、svn help2、svn add3、svn blame4、svn cat5、svn changelist6、svn checkout7、svn cleanup8、svn commit9、svn copy10、svn delete11、svn diff12、svn export13、svn help14、svn import15、svn info16、svn list17、svn lock18、svn log19、svn merge…

VClient 无法连接Vcenter
前一段在一台windows server 2008 R2上使用local Administrator 安装了VCenter 4.1. 一开始使用VClient 是可以登录的,但是重新启动这台安装有VCenter 的Server 之后就连接不到了。为什么呢? 打开这台Windows Server 2008 查看服务发现SQL 和 VM 都有服务…

智能音箱玩出新花样?这家公司推出2699元的智能虚拟机器人
家居控制、备忘提醒、媒体播放、智能聊天… …如今,AI 应用备受瞩目,智能虚拟机器人也成为了 AI 应用的新方向。 5 月 20 日下午,专注于虚拟机器人研发、平台软件开发运用及销售为一体的公司欧博思发布了 AI BOX 智能虚拟机器人产品。 乍一…

干货 :数据可视化的10个关键术语
2019独角兽企业重金招聘Python工程师标准>>> Format 交互方式 交互式可视化允许您修改,操作和探索计算机显示的数据。绝大多数交互式可视化系统在计算机网络上,但越来越多出现在平板电脑和智能手机上。相比之下,静态可视化只显示单…
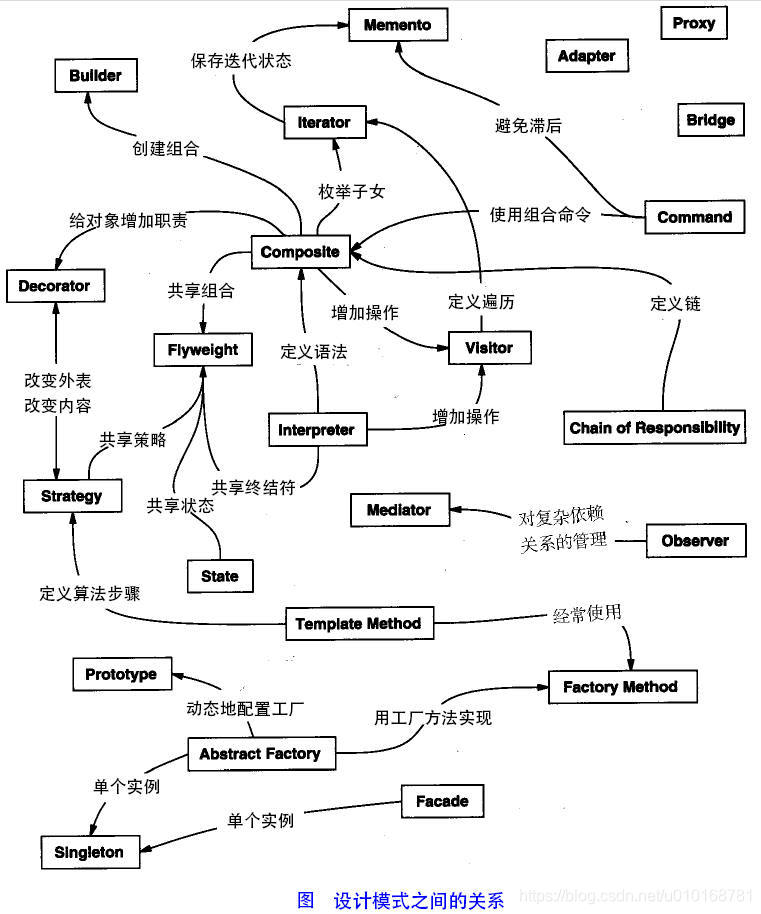
【设计模式】三大类:创建型模式、结构型模式、行为型模式
1 创建型模式 本人理解:以C为例,创建对象时,用关键字new来创建(实例化)对象。用一个函数或类将new的过程封装起来,就是创建型模式。 《设计模式》中的描述: 创建型模式抽象了实例化过程。它们…
