揭开「拓扑排序」的神秘面纱
作者 | 小齐本齐
责编 | Carol
来源 | 码农田小齐
Topological sort 又称 Topological order,这个名字有点迷惑性,因为拓扑排序并不是一个纯粹的排序算法,它只是针对某一类图,找到一个可以执行的线性顺序。
这个算法听起来高大上,如今的面试也很爱考,比如当时我在面我司时有整整一轮是基于拓扑排序的设计。
但它其实是一个很好理解的算法,跟着我的思路,让你再也不会忘记她。
有向无环图
刚刚我们提到,拓扑排序只是针对特定的一类图,那么是针对哪类图的呢?
答:Directed acyclic graph (DAG),有向无环图。即:
这个图的边必须是有方向的;
图内无环。
那么什么是方向呢?
比如微信好友就是有向的,你加了他好友他可能把你删了你却不知道。。。那这个朋友关系就是单向的。。
什么是环?环是和方向有关的,从一个点出发能回到自己,这是环。
所以下图左边不是环,右边是。
那么如果一个图里有环,比如右图,想执行1就要先执行3,想执行3就要先执行2,想执行2就要先执行1,这成了个死循环,无法找到正确的打开方式,所以找不到它的一个拓扑序。
总结:
如果这个图不是 DAG,那么它是没有拓扑序的;
如果是 DAG,那么它至少有一个拓扑序;
反之,如果它存在一个拓扑序,那么这个图必定是 DGA.
所以这是一个充分必要条件。
拓扑排序
那么这么一个图的「拓扑序」是什么意思呢?
我们借用百度百科[1]的这个课程表来说明。
这里有 9 门课程,有些课程是有先修课程的要求的,就是你要先学了「最右侧这一栏要求的这个课」才能再去选「高阶」的课程。
那么这个例子中拓扑排序的意思就是:
就是求解一种可行的顺序,能够让我把所有课都学了。
那怎么做呢?
首先我们可以用图来描述它,图的两个要素是顶点和边,那么在这里:
顶点:每门课
边:起点的课程是终点的课程的先修课
画出来长这个样:
这种图叫 AOV (Activity On Vertex) 网络,在这种图里:
顶点:表示活动;
边:表示活动间的先后关系
所以一个 AOV 网应该是一个 DAG,即有向无环图,否则某些活动会无法进行。
那么所有活动可以排成一个可行线性序列,这个序列就是拓扑序列。
那么这个序列的实际意义是:
按照这个顺序,在每个项目开始时,能够保证它的前驱活动都已完成,从而使整个工程顺利进行。
回到我们这个例子中:
我们一眼可以看出来要先学 C1, C2,因为这两门课没有任何要求嘛,大一的时候就学呗;
大二就可以学第二行的 C3, C5, C8 了,因为这三门课的先修课程就是 C1, C2,我们都学完了;
大三可以学第三行的 C4, C9;
最后一年选剩下的 C6, C7。
这样,我们就把所有课程学完了,也就得到了这个图的一个拓扑排序。
注意,有时候拓扑序并不是唯一的,比如在这个例子中,先学 C1 再学 C2,和先 C2 后 C1 都行,都是这个图的正确的拓扑序,但这是两个顺序了。
所以面试的时候要问下面试官,是要求解任意解,还是列出所有解。
我们总结一下,
在这个图里的边表示的是一种依赖关系,如果要修下一门课,就要先把前一门课修了。
这和打游戏里一样一样的嘛,要拿到一个道具,就要先做 A 任务,再完成 B 任务,最终终于能到达目的地了。
算法详解
在上面的图里,大家很容易就看出来了它的拓扑序,但当工程越来越庞大时,依赖关系也会变得错综复杂,那就需要用一种系统性的方式方法来求解了。
那么我们回想一下刚刚自己找拓扑序的过程,为什么我们先看上了 C1, C2?
因为它们没有依赖别人啊,
也就是它的入度为 0.
入度:顶点的入度是指「指向该顶点的边」的数量;
出度:顶点的出度是指该顶点指向其他点的边的数量。
所以我们先执行入度为 0 的那些点,
那也就是要记录每个顶点的入度。
因为只有当它的 入度为 0 的时候,我们才能执行它。
在刚才的例子里,最开始 C1, C2 的入度就是 0,所以我们可以先执行这两个。
那在这个算法里第一步就是得到每个顶点的入度。
Step0: 预处理得到每个点的入度
我们可以用一个 HashMap 来存放这个信息,或者用一个数组会更精巧。
在文中为了方便展示,我就用表格了:
Step1
拿到了这个之后,就可以执行入度为 0 的这些点了,也就是 C1, C2.
那我们把可以被执行的这些点,放入一个待执行的容器里,这样之后我们一个个的从这个容器里取顶点就好了。
至于这个容器究竟选哪种数据结构,这取决于我们需要做哪些操作,再看哪种数据结构可以为之服务。
那么首先可以把[C1, C2]放入容器中,
然后想想我们需要哪些操作吧!
我们最常做的操作无非就是把点放进来,把点拿出去执行了,也就是需要一个 offer 和poll操作比较高效的数据结构,那么 queue 就够用了。
(其他的也行,放进来这个容器里的顶点的地位都是一样的,都是可以执行的,和进来的顺序无关,但何必非得给自己找麻烦呢?一个常规顺序的简简单单的 queue 就够用了。)
然后就需要把某些点拿出去执行了。
【划重点】当我们把 C1 拿出来执行,那这意味这什么?
答:意味着「以 C1 为顶点」的「指向其他点」的「边」都消失了,也就是 C1 的出度变成了 0.
如下图,也就是这两条边可以消失了。
那么此时我们就可以更新 C1 所指向的那些点也就是 C3 和 C8 的 入度 了,更新后的数组如下:
那我们这里看到很关键的一步,C8 的入度变成了 0!
也就意味着 C8 此时没有了任何依赖,可以放到我们的 queue 里等待执行了。
此时我们的 queue 里就是:[C2, C8].
Step2
下一个我们再执行 C2,
那么 C2 所指向的 C3, C5 的 入度-1,
更新表格:
也就是 C3 和 C5 都没有了任何束缚,可以放进 queue 里执行了。
queue 此时变成:[C8, C3, C5]
Step3
那么下一步我们执行 C8,
相应的 C8 所指的 C9 的入度-1.
更新表格:
那么 C9 没有了任何要求,可以放进 queue 里执行了。
queue 此时变成:[C3, C5, C9]
Step4
接下来执行 C3,
相应的 C3 所指的 C4 的入度-1.
更新表格:
但是 C4 的入度并没有变成 0,所以这一步没有任何点可以加入 queue。
queue 此时变成 [C5, C9]
Step5
再执行 C5,
那么 C5 所指的 C4 和 C6 的入度- 1.
更新表格:
这里 C4 的依赖全都消失啦,那么可以把 C4 放进 queue 里了:
queue = [C9, C4]
Step6
然后执行 C9,
那么 C9 所指的 C7 的入度- 1.
这里 C7 的入度并不为 0,还不能加入 queue,
此时 queue = [C4]
Step7
接着执行 C4,
所以 C4 所指向的 C6 和 C7 的入度-1,
更新表格:
C6 和 C7 的入度都变成 0 啦!!把它们放入 queue,继续执行到直到 queue 为空即可。
总结
好了,那我们梳理一下这个算法:
数据结构这里我们的入度表格可以用 map 来存放
Map: <key = Vertex, value = 入度>
但实际代码中,我们用一个 int array 来存储也就够了,数组的 index 表示每个顶点,数组里的数值来表示每个顶点的入度,这样比 Map 更精巧。
然后用了一个普通的 queue,用来存放可以被执行的那些 node.
过程
我们把入度为 0 的那些顶点放入 queue 中,然后通过每次执行 queue 中的顶点,就可以让依赖这个被执行的顶点的那些点的 入度-1,如果有顶点的入度变成了 0,就可以放入 queue 了,直到 queue 为空。
细节
这里有几点实现上的细节:
当我们 check 是否有新的顶点的 入度 == 0 时,没必要过一遍整个 map 或者数组,只需要 check 刚刚改动过的就好了。
另一个是如果题目没有给这个图是 DAG 的条件的话,那么有可能是不存在可行解的,那怎么判断呢?很简单的一个方法就是比较一下最后结果中的顶点的个数和图中所有顶点的个数是否相等,或者加个计数器,如果不相等,说明就不存在有效解。所以这个算法也可以用来判断一个图是不是有向无环图。
很多题目给的条件可能是给这个图的 edge list,也是表示图的一种常用的方式。那么给的这个 list 就是表示图中的边。这里要注意审题哦,看清楚是谁 depends on 谁。其实图的题一般都不会直接给你这个图,而是给一个场景,需要你把它变回一个图。
时间复杂度
注意:对于图的时间复杂度分析一定是两个参数,因为图的顶点数和边的数量没有固定的关系,然而面试的时候很多同学张口就是 O(n)...
对于有 v 个顶点和 e 条边的图来说,
第一步,预处理得到 map 或者 array,需要过一遍所有的边才行,所以是 O(e);
第二步,把 入度 == 0 的点入队出队的操作是 O(v),如果是一个 DAG,那所有的点都需要入队出队一次;
第三步,每次执行一个顶点的时候,要把它指向的那条边消除了,这个总共执行 e 次;
总:O(v + e)
空间复杂度
用了一个数组来存所有点的 indegree,之后的 queue 也是最多把所有的点放进去,所以是 O(v).
代码
关于这课程排序的问题,Leetcode 上有两道题,一道是 207,问你能否完成所有课程,也就是问拓扑排序是否存在;另一道是 210 题,是让你返回任意一个拓扑顺序,如果不能完成,那就返回一个空 array。
这里我们以 210 这道题来写,更完整也更常考一些。
这里给的 input 就是我们刚刚说到的 edge list.
Example 1. Input: 2, [[1,0]]
Output: [0,1]
Explanation: 这里一共2门课,1的先修课程是0. 所以正确的选课顺序是[0, 1].Example 2. Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]
Explanation: 这里这个例子画出来如下图
Example 3. Input: 2, [[1,0],[0,1]]
Output: null
Explanation: 这课没法上了class Solution {public int[] findOrder(int numCourses, int[][] prerequisites) {int[] res = new int[numCourses];int[] indegree = new int[numCourses];// get the indegree for each coursefor(int[] pre : prerequisites) {indegree[pre[0]] ++;}// put courses with indegree == 0 to queueQueue<Integer> queue = new ArrayDeque<>();for(int i = 0; i < numCourses; i++) {if(indegree[i] == 0) {queue.offer(i);}}// execute the courseint i = 0;while(!queue.isEmpty()) {Integer curr = queue.poll();res[i++] = curr;// remove the pre = currfor(int[] pre : prerequisites) {if(pre[1] == curr) {indegree[pre[0]] --;if(indegree[pre[0]] == 0) {queue.offer(pre[0]);}}}}return i == numCourses ? res : new int[]{};}
}
还是附上题目吧,just in case, if you want to see the details.
另外,拓扑排序还可以用 DFS - 深度优先搜索 来实现,限于篇幅就不在这里展开了,大家可以参考GeeksforGeeks[2]的这个资料。
实际应用
我们上文已经提到了它的一个 use case,就是选课系统,这也是最常考的题目。
而拓扑排序最重要的应用就是关键路径问题,这个问题对应的是 AOE (Activity on Edge) 网络。
AOE 网络:顶点表示事件,边表示活动,边上的权重来表示活动所需要的时间。
AOV 网络:顶点表示活动,边表示活动之间的依赖关系。
在 AOE 网中,从起点到终点具有最大长度的路径称为关键路径,在关键路径上的活动称为关键活动。AOE 网络一般用来分析一个大项目的工序,分析至少需要花多少时间完成,以及每个活动能有多少机动时间。
具体是怎么应用分析的,大家可以参考这个视频[3] 的14分46秒,这个例子还是讲的很好的。
其实对于任何一个任务之间有依赖关系的图,都是适用的。
比如 pom 依赖引入 jar 包时,大家有没有想过它是怎么导进来一些你并没有直接引入的 jar 包的?比如你并没有引入 aop 的 jar 包,但它自动出现了,这就是因为你导入的一些包是依赖于 aop 这个 jar 包的,那么 maven 就自动帮你导入了。
其他的实际应用,知乎上专门有个帖子[4],在这里我总结一下:
语音识别系统的预处理;
管理目标文件之间的依赖关系,就像我刚刚说的 jar 包导入;
深度学习中的网络结构处理。
如有其他补充,欢迎大家在评论区不吝赐教。
以上就是本文的全部内容了,拓扑排序是非常重要也是非常爱考的一类算法,面试大厂前一定要熟练掌握。
今日福利
遇见大咖
由 CSDN 全新专为技术人打造的高端对话栏目《大咖来了》来啦!
CSDN 创始人&董事长、极客帮创投创始合伙人蒋涛携手京东集团技术副总裁、IEEE Fellow、京东人工智能研究院常务副院长、深度学习及语音和语言实验室负责人何晓冬,来也科技 CTO 胡一川,共话中国 AI 应用元年来了,开发者及企业的路径及发展方向!
戳链接或点击阅读原文,直达报名:https://t.csdnimg.cn/uZfQ
相关文章:
Spring源码分析【6】-ThreadLocal的使用和源码分析
Spring代码使用到了ThreadLocal java.lang.ThreadLocal.set getMap java.lang.Thread.threadLocals定义 回到set 如果map为null 则createMap

《软件的破解》
本人根据自己的经验简单给大家谈一谈。这些问题对于初学者来说常常是很需要搞明白的,根据我自己的学习经历,如果你直接照着很多破解教程去学习的话,多半都会把自己搞得满头的雾水,因为有很多的概念要么自己不是很清楚,…

php级别鉴定
一、PHP初级程序员薪资水平:4000.00--8000.00(RMB/月)~HTML设计与应用~DIVCSS~PHP基础~MySQL基础~PHP高级~CMS系统二、PHP中级程序员 薪资水平:8000.00--12000.00(RMB/月)~PHP面向对象~MySQL高级~Smarty模板…
Spring源码分析【7】-Spring 模板页和JSP文件的编译
org.apache.jasper.servlet.JspServletWrapper.service org.apache.jasper.JspCompilationContext.compile org.apache.jasper.JspCompilationContext.createCompiler org.apache.jasper.compiler.Compiler.isOutDated 判断文件是否存在 ..\Apache\apache-tomcat-8.0.36\w…

Distinction Between Strategy and Decorator
首先看Strategy和Decorator在GoF的《Design Patterns》的intent Decorator (1)intent: Attach additional responsibilities to an object dynamically.Decorators provide a flexible alternative to subclassing for extending functionality. (2)UML Diagram: Strategy (1)i…
我竟然混进了Python高级圈子!
现如今,计算机科学、人工智能、数据科学已成为技术发展的主要推动力。无论是要翻阅这些领域的文章,还是要参与相关任务,你马上就会遇到一些拦路虎:想过滤垃圾邮件,不具备概率论中的贝叶斯思维恐怕不行;想试…

unity3d中旋转
自转是Rotate,绕转是RotateAround,LookAt旋转物体自身,使其正面朝向目标点以上操作都在transform中完成转载于:https://blog.51cto.com/568464209/1764050

Java常用方法
1. 把Strings转换成int和把int转换成StringString a String.valueOf(2); //integer to numeric string int i Integer.parseInt(a); //numeric string to an int String a String.valueOf(2); //integer to numeric stringint i Integer.parseInt(a); //numeric string …
request.getSession(false)到底返回什么
HttpSession session request.getSession(false); 很明显传false如果session不存在返回Null。
洞察疫情,微软推出新冠数据分析网站COVID Insights
来源 | 微软研究院AI头条COVID Insights 网站功能亮点持续数月的新冠疫情一路肆虐、席卷全球,世界各地的科研人员都在为此奋战,希望通过最先进的技术逐步揭开新冠病毒的神秘面纱。近日,微软亚洲研究院的研究人员基于在计算生物学、数据分析等…

LINUX 查找tomcat日志关键词
#查询catalina.out日志文件中的关键词为2016-04-13 11:26:00的日志信息grep -C 10 2016-04-13 11:26:00 catalina.out |more解释:grep :查询,筛选-C : grep的-A, -B, -C选项分别可以显示匹配行的后,前,后前多少行内容:10 …

转帖 javascript事件监听
原帖地址: http://www.cnblogs.com/AganCN/archive/2008/05/24/1206272.html 考虑这样的情形在IE浏览中处理,需要响应页面的按钮点击事件,有哪些方法呢?(1)onclick属性添加事件处理函数 <javascript>…
推荐系统发展的六大影响因子 | 深度
作者丨gongyouliu来源 | 大数据与人工智能(ID: ai-big-data)随着科学技术的进步,移动互联网快速发展,手机越来越便宜,拥有智能手机不再是一件遥不可及的事情,互联网用户规模已接近增长的顶点。摄像头和信息…
Spring源码分析【9】-SpringSecurity密码Remove原理
很明显代码已经说了认证完成移除credentials和其他某些安全数据 // Authentication is complete. Remove credentials and other secret data // from authentication org.springframework.security.authentication.ProviderManager.authenticate package org.springframewo…

Linux --进程间通信--共享内存
一、共享内存共享内存是最高效的通信方式,因为不需要一个进程先拷贝到内核,另一个进程在存内核中读取。二、 ipcs -m 查看共享内存ipcrm -m 删除共享内存三、主要函数shmget 创建shmctl 删除shmat 挂接shmdt 取消挂接********* man 函数名 查看*****四、…
如何用 Slack 和 Kubernetes 构建一个聊天机器人?| 附代码
作者 | Alexander Kainz译者 | 天道酬勤,责编 | Carol出品 | AI科技大本营(ID:rgznai100)ChatOps可以让你使用基于聊天的接口来管理DevOps任务。本文主要让我们了解如何使用Slack构建一个简单的机器人来控制Kubernetes集群。最后我们可以使用…
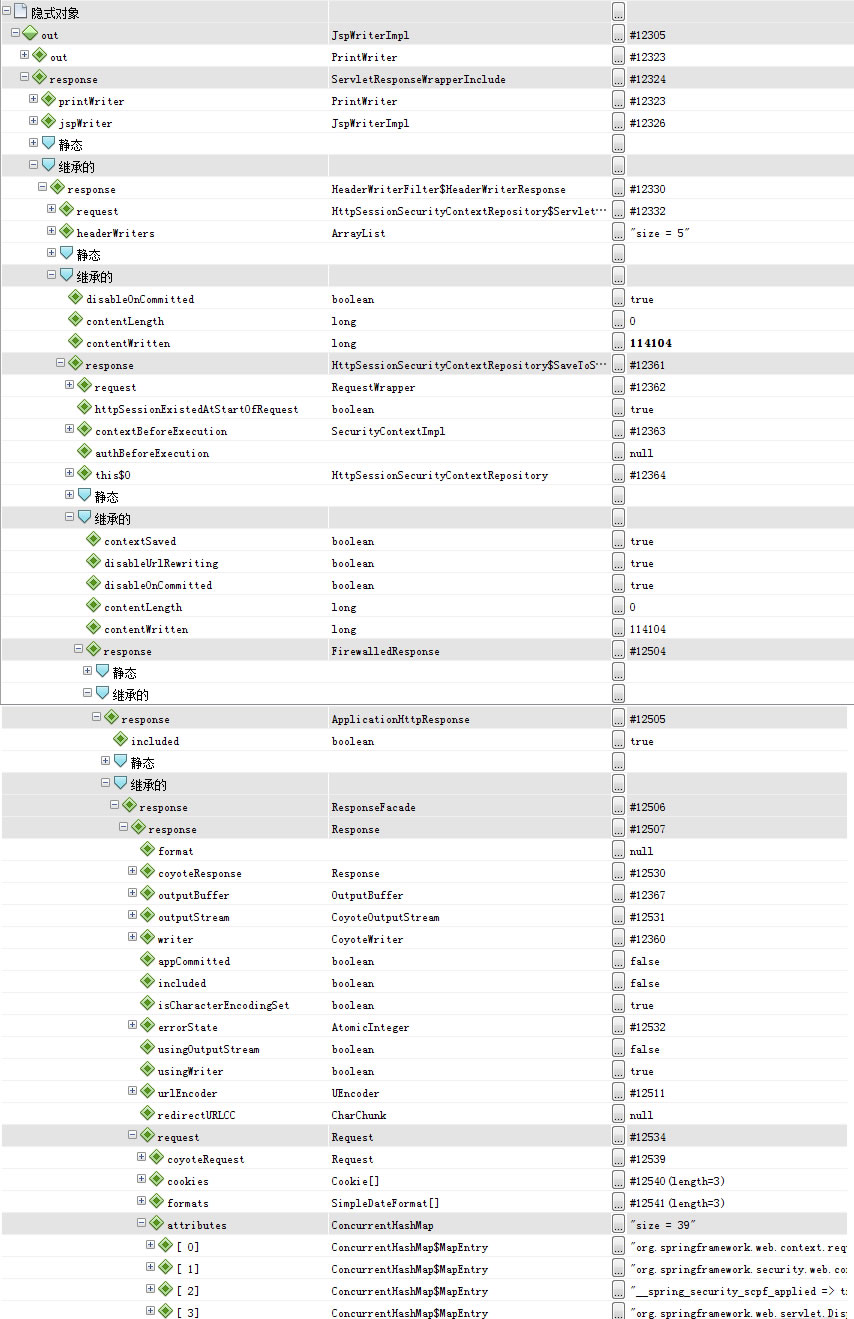
在jsp调试后端绑定对象
在jsp调试后端绑定对象,这个调用层次非常深

一行代码轻松实现拖动效果
写JS实现拖动需要一大堆不便维护的代码,实属麻烦,Google了大半天,发现了一个优秀的Jquery插件EasyDrag,只需要一行代码便可轻松在主流浏览器上 实现拖动效果. $(document).ready( function() { $("#divPanel"…
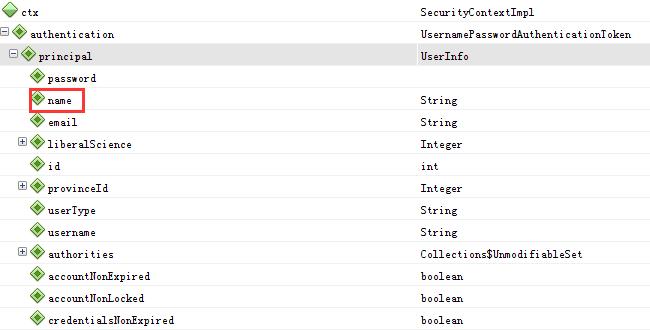
Spring源码分析【8】-分布式环境SpringSecurity保持用户会话
1.SpringSecurity的权限控制流程是这样的:用户登录,基础信息UserInfo存在SpringSecurity的ThreadLocal里。 下面是contextHolder对象: final class ThreadLocalSecurityContextHolderStrategy implementsSecurityContextHolderStrategy {// ~…

【Android游戏开发之七】(游戏开发中需要的样式)再次剖析游戏开发中对SurfaceView中添加组件方案!...
本站文章均为 李华明Himi 原创,转载务必在明显处注明: 转载自【黑米GameDev街区】 原文链接: http://www.himigame.com/android-game/308.html 各位童鞋请你们注意:surfaceview中确实有 onDraw这个方法,但是surfaceview不会自己去调用&#x…
“华为云杯”2020深圳开放数据应用创新大赛线上推介会成功举办,让深圳大数据在全球“跑”起来...
4月30日下午,“华为云杯”2020深圳开放数据应用创新大赛第三场线上推介会完美落幕。至此,从4月23日开始的三场云端推介会全部结束,全球各数字平台总观看量1000多万人次。深圳市政务服务数据管理局副局长王耀文、深圳市南山区副区长练聪、南山…

学习OpenCV——配置CUDA环境
大家都把GPU&CUDA说的很NB狠NB,于是,下一步想通过GPU加速程序运行。这一个星期,都在配置OpenCV的CUDA环境,今天终于以失败告终,原因是实验室的机器显卡不支持CUDA。。。伤不起啊,一星期啊!&…
NLP带来的“科幻感”超乎你的想象 - ACL2020论文解读
来源 | 京东智联云开发者责编 | Carol近些年,人工智能无疑是信息技术领域最热门的技术之一。人工智能战胜世界围棋冠军、人工智能战胜游戏高手、人工智能医生看病会诊……不断进步的科技正推动着人工智能从一个无法实现的幻想,不断突破人类的想象&#x…

Vsftp 安装配置(转)
转:http://www.cnblogs.com/qingfeng2010/archive/2010/12/26/1917121.html 1.查看是否安装vsftprpm –qa|grep vsftpd 如果出现 vsftpd-2.0.5-16.el5_5.1 说明已经安装 vsftp 安装vsftp yum -y installvsftpd 2.测试 是否安装成功 (ip 改成自己啊,…

事务隔离机制原理分析以及是否可以防止订单超卖
事务的隔离机制是指: Read Uncommitted(读取未提交内容) Read Committed(读取提交内容) Repeatable Read(可重读) Serializable(可串行化) 具体的解释最经典的MySQL书《…

PHP中file_exists与is_file,is_dir的区别介绍
PHP中file_exists与is_file,is_dir的区别介绍作者: 字体:[增加 减小] 类型:转载 时间:2012-09-12 我要评论很显然file_exists是受了asp的影响,因为asp不但有fileExists还有folderExists,driverExists,那么P…
推荐算法工程师的成长之道
作者 | gongyouliu来源 | 大数据与人工智能(ID: ai-big-data)本文,作者会基于自己的实践经验讲述推荐算法工程师的成长之道,这里的“道”有发展路径和道(道理、方法论、经验、智慧)两层意思。所以本文除了讲解推荐算法工程师的成长…
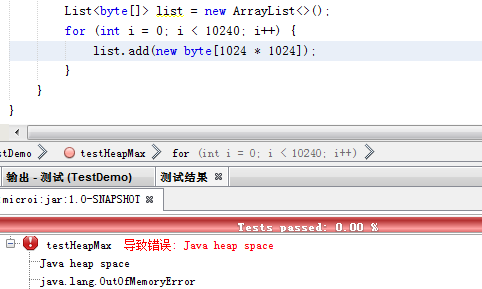
JVM内存溢出的几种情形
1.堆溢出 原因:大量对象占据了堆空间,而这些对象都有强引用导致无法回收,当对象大小之和>Xmx参数指定的堆大小时导致溢出! List<byte[]> list new ArrayList<>();for (int i 0; i < 10240; i) {list.add(new…

Android Market 链接的生成与分享
通过Java包名直接定位到你的App http://market.android.com/details?id<java包名> 或者 market://details?id<java包名> 范例:market://details?idcom.skyd.luckywheel 这将直接在菜市场中显示你的App详细介绍页。 通过Java包名搜索App http://marke…

Centos6/7下静默安装oracle10g
Centos6/7下静默安装Oracle10g 远程安装oracle10g,通过网上资料,不断摸索成功安装。先在本地虚拟机Centos7上做实验,快照恢复快照恢复,安装了几十次成功之后,再在服务器Centos6上安装,(6和7还是有区别的,比…
