作者:桂。
时间:2017-03-27 20:26:17
链接:http://www.cnblogs.com/xingshansi/p/6628785.html
声明:欢迎被转载,不过记得注明出处哦~

【读书笔记06】
前言
看到西蒙.赫金的《自适应滤波器原理》第四版第四章:最速下降算法。最速下降法、拟牛顿法等都是求解准则函数(即无约束优化问题)的算法,这就需要有一个前提:怎样得到无约束准则函数?联想到之前看维纳滤波:无约束维纳滤波、约束维纳滤波,提到了拉格朗日乘子,将有限制条件的优化问题转化为无限制的优化问题,可见拉格朗日乘子搭建了一个桥梁:将有限制的准则函数,转化为无限制准则函数,进而借助最速下降法、拟牛顿法等求参算法进行求解,在这里汇总一下拉格朗日乘子法是有必要的,全文包括:
1)含有等式约束的拉格朗日乘子法;
2)拉格朗日对偶方法;
内容为自己的学习记录,其中多有参考他人,最后一并给出链接。
一、含有等式约束拉格朗日乘子法
对于含有约束的优化问题,可以在约束域内对准则函数搜索最优解,但如果约束较为复杂搜索起来显然不那么容易,如果借助某种方式将约束问题转化为无约束问题,求解则更为方便一些,这也是拉格朗日乘子法的魅力所在。本段内容为维纳滤波一文的开头部分。
A-只含一个等式约束的最优化
实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数,约束条件是:
${{{\bf{w}}^H}{\bf{s}} = g}$
其中$\bf{s}$是已知向量,$g$是复常数。例如在波束形成应用中${\bf{w}}$表示各传感器输出的一组复数权值,$\bf{s}$是一个旋转向量。假设该问题是一个最小化问题,令$c\left( {\bf{w}} \right) = {{\bf{w}}^H}{\bf{s}} - g = 0 + j0$可以描述为:
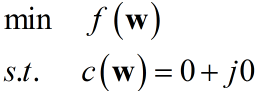
所谓拉格朗日乘子法,就是引入拉格朗日乘子:将上述约束最小化问题转化为无约束问题,定义一个新的实函数:
$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\lambda _1}{\mathop{\rm Re}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right] + {\lambda _2}{\mathop{\rm Im}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right]$
现在定义一个复拉格朗日乘子:
$\lambda = {\lambda _1} + {\lambda _2}$
$h({\bf{w}})$改写为:
$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\mathop{\rm Re}\nolimits} \left[ {{\lambda ^*}c\left( {\bf{w}} \right)} \right]$
至此,无约束优化问题转化完成,利用偏导求参即可,其实这是一个简化的形式,分别求解$\lambda _1$、$\lambda _2$也是一样的。
B-包含多个等式约束的最优化
实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数,约束条件是:
${{{\bf{w}}^H}{\bf{s_k}} = g_k}$
其中$k = 1,2...K$,方法同单个约束情况相同,求解伴随方程:
$\frac{{\partial f}}{{\partial {{\bf{w}}^*}}} + \sum\limits_{k = 1}^K {\frac{\partial }{{\partial {{\bf{w}}^*}}}\left( {{\mathop{\rm Re}\nolimits} \left[ {\lambda _k^*{c_k}\left( {\bf{w}} \right)} \right]} \right)} = {\bf{0}}$
此时与多个等式约束联合成方程组,这个方程组定义了${\bf{w}}$和拉格朗日乘子${\lambda _1}$、${\lambda _2}$...${\lambda _K}$的解。
如果含有不等式约束,或者说既有等式约束、又有不等式约束呢?
二、拉格朗日对偶问题(Lagrange duality)
A-原始问题
给出约束优化问题模型:

其中${h_i}\left( x \right) = 0,\;i = 1,...q$也可写成矩阵形式:${\bf{Ax}} = {\bf{b}}$.该模型为原始问题。
该模型利用拉格朗日乘子可以松弛为无约束优化问题:
$\min \;\;L\left( {x,\lambda ,v} \right) = {f_0}\left( x \right) + \sum\limits_{i = 1}^m {{\lambda _i}{f_i}\left( x \right) + \sum\limits_{i = 1}^q {{v_i}{h_i}\left( x \right)} } $
该模型为对偶问题。约束${{\lambda _i}} \ge 0$,则$\sum\limits_{i = 1}^m {{\lambda _i}{f_i}\left( x \right)} \le 0$,即:
$L\left( {x,\lambda ,v} \right) \le {f_0}\left( x \right)$
为了逼近$f_0(x)$,首先针对${\lambda ,v}$对其最大化:
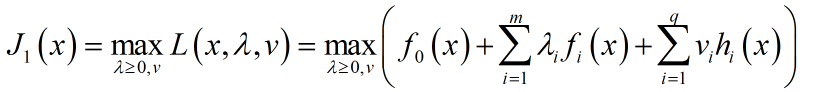
但由于该问题只是对${\lambda ,v}$的约束,无法避免违反约束$f_i(x)>0$,从而导致$J_1(x)$无穷大:

可以看出将$J_1(x)$极小化即可得解:
![]()
这是原始约束极小化问题变成无约束极小化问题后的代价函数,简称原始代价函数。定义原始约束极小化问题的最优解:
![]()
这就是原始最优解(Optimal primal value).
给出两点凸函数性质:
性质1:无约束凸函数$f(x)$的任何局部极小点$x^*$都是该函数的一个全局极小点;
性质2:如果$f(x)$是强凸函数,则极小化问题$\min f(x)$可解,且其解$x$唯一。
但这里存在一个问题:如果$f_0(x)$不是凸函数(也非凹),便没有性质1、性质2,即使设计了优化算法,可以得到某个局部极值点,但不能保证它是一个全局极值点。
如果可以:将非凸目标函数的极小化转换成凹目标函数的极大化,局部极值点便是全局极值点。实现转换的手段便是——对偶方法。
B-对偶方法
考虑构造另一个目标函数:
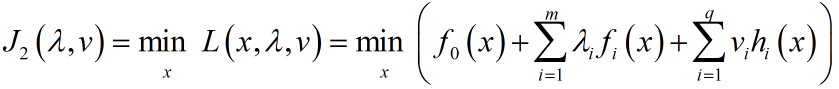
这个模型是原问题的对偶问题,根据上式:
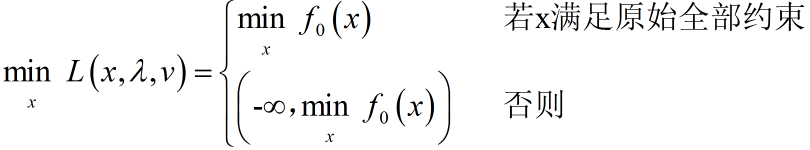
得到对偶目标函数:
![]()
由此可见:${J_D}\left( {\lambda ,v} \right)$是$x$的凹函数,即使$f_0(x)$不是凸函数(凹函数同理,本文仅以凸为例).此时任何一个局部极值点都是一个全局极值点。至此:原约束极小化问题转化为对偶目标函数的无约束极大化算法设计,这一方法就是:拉格朗日对偶法。
记对偶目标函数最优值(简称对偶最优值)为:
${d^*} = {J_D}\left( {{\lambda ^*},{v^*}} \right)$
给出两点性质:$\max$为凸函数,$\min$为凹函数,与$f(.)$内部形式无关。
性质1:函数$f\left( x \right) = \max$ { ${x_1},{x_2},...,{x_n}$} 在${{\bf{R}}^n}$上是凸函数。
证明:
对任意$0 \le \theta \le 1$,函数$f(x) = \max_i x_i$满足:
性质2:函数$f\left( x \right) = \min$ { ${x_1},{x_2},...,{x_n}$} 在${{\bf{R}}^n}$上是凹函数。
证明与上同。
C-对偶目标函数与原目标函数关系
首先写出原最优值与对偶最优值的关系:
![]()
字面理解:瘦子里的胖子,体重不会超过胖子里的瘦子。分析其理论:
对于极值点$x^*$,恒有:
可以看出$\mathop {\min \;}\limits_x L\left( {x,\lambda ,v} \right)$是$p^*$的下界,而$d^*$自然是下界中最大的那个(最接近原始最优解):
事实上对任何一个非负实值函数$f(x,y)$,总有:
既然是下界,就必然有差距,定义$p^*-d^*$为对偶间隙(duality gap).我们称${p^*} \ge {d^*}$为弱对偶性(weak duality).
D-Slater定理
首先给出凸优化定义:
形式:
其中$h_i(x)$是形如$h_i(x) = a^{T}_ix = b_i$的仿射函数。相对上面讨论的优化问题,凸优化问题有三个附加要求:
- 目标函数必须是凸的;
- 不等式函数约束必须是凸的;
- 等式约束必须是仿射的;
凹凸可以转化:对于凹函数$f$,$-f$即为凸函数。
与weak duality对应的是strong duality(强对偶性):${p^*} = {d^*}$,给出Slater定理:
如果原不等式优化问题为凸优化问题,且满足Slater条件:
- $f_i(x) < 0$,$i=1,2,...,m$;
- $h_i(x) = 0$,$i=1,2,...,q$;
则${p^*} = {d^*}$。
E-KKT条件
首先给出KKT(Karush-Kuth-Tucker,KKT)条件:

1)、2)、3)都容易理解,对于4)主要是防止$f_i(x)>0$的出现,从而设置一个障碍;5)因为$x^*$是最优值,只要偏导存在,该式成立——平稳点存在。
可以得出:
对于一般性优化问题:
- KKT是原问题转化为对偶优化问题的必要条件(局部极小解一阶必要条件);
- 如果约束条件满足凸优化定义,仅仅$f_0(x)$为一般函数,则 原问题准则函数 和 对偶准则函数 的极值点通常不一致。
对于凸优化问题:
- 满足KKT条件的店,那么它们分别是 原问题准则函数 和 对偶准则函数 的极值点并且 strong duality 成立。
证明可以参考:pluskid大神的文章。
总结一下:
- 对偶问题可以将准则函数转化为凸函数;
- KKT为凸优化判定提供了依据;
- 对偶转化、KKT以及Slater并不限于凸优化问题。
参考:
- 张贤达:矩阵分析与应用
- http://blog.pluskid.org/?p=702