《计算机组成原理》----2.6 浮点数
本节书摘来自华章出版社《计算机组成原理》一书中的第2章,第2.6节, 作 者 Computer Organization and Architecture: Themes and Variations[英]艾伦·克莱门茨(Alan Clements) 著,沈 立 王苏峰 肖晓强 译, 更多章节内容可以访问云栖社区“华章计算机”公众号查看。
2.6 浮点数
介绍了整数之后,下一步就是讨论浮点运算,即实数之间的运算。实数是所有有理数和无理数的集合。浮点运算能够让人们处理科学应用(与金融或商业应用相对)中很大的和很小的数。浮点运算不像整数运算,它的计算结果一般是不确定的。一块芯片上的浮点计算结果也许与另一块芯片上的不同。后面将解释为什么浮点运算无法获得确定的答案,并讨论一些程序员必须了解的陷阱。
n位字长的计算机能够处理值为0~2n-1的单字长无符号整数。更大的整数可以通过将多个字链接在一起来表示。例如,一台32位的计算机可以将两个32位字拼接在一起以处理64位数(一个表示64位数的高半部分,另一个表示它的低半部分)。科学家和工程师经常会处理值范围极大的数(例如,从电子的质量到星体的质量)。这些数被表示为浮点数并进行处理,之所以这样叫是因为小数点在数中的位置并不是固定的。一个浮点数值分两部分存储:数值以及小数点在数值中的位置。
浮点数表示也被称作“科学计数法”,因为科学家用它来表示很大或很小的数。1.2345×1020,0.4599×10-50,-8.5×103等都是十进制浮点数。在十进制运算中,科学计数法表示的数字被写成尾数×10指数的形式,这里尾数表示这个数,而指数则以10的整数幂为倍数将其扩大或缩小。
二进制浮点数则被表示为尾数×2指数的形式。例如,101010.1111102可被表示为1.01010111110×25,这里尾数为1.01010111110,指数为5(用8位二进制数表示为00000101)。今天,术语mantissa(尾数)已被替换为significand以表示浮点数中有效位的位数。由于浮点数被定义为两个值的积,浮点数的表示并不唯一;例如10.110×24 = 1.0110×25。
多年以来,计算机系统使用了很多不同的方法表示浮点数的尾数和指数。20世纪70年代,一种标准的浮点数表示方法快速地取代了大多数系统自有的格式。IEEE 754浮点数标准提供了3种浮点数表示:32位单精度浮点数,64位双精度浮点数,以及128位四精度浮点数。
1.规格化浮点数
IEEE 754浮点数的尾数总是规格化的(除非它等于0),其范围为1.000…0×2e到1.111…1×2e,这里e为指数。规格化浮点数的最高位总是1。规格化使尾数的所有位都是有效的,因而尾数的精度最高。若某个浮点计算的结果为0.110…×2e,它应被规格化为1.10…×2e-1。同样,结果10.1…×2e应被规格化为1.01…×2e+1。
尾数规格化充分利用了可用的最大精度。例如,一个8位非规格化的尾数0.0000101只有4个有效位,而规格化后的8位尾数1.0100011则有8个有效位。
2.偏置指数
IEEE 754浮点数的尾数被表示为符号和数值的形式,即用一个符号位表示它是正数还是负数。它的指数则用偏置方式表示,即给真正的指数加上一个常数。假定所用的指数为8位,偏置值为127。若一个数的指数为0,它被保存为0 + 127 = 127。若指数为-2,则被保存为-2 + 127 = 125。实数1010.1111规格化的结果为+1.010111×23。指数为+3,将被保存为3 + 127 = 130;即13010或用二进制表示为10000010。
这种用偏置表示指数的方法的优点在于,最小的负指数被表示为0。若不采用这种方法,0的浮点表示为0.0…0×2最小负指数。采用偏置指数之后,0就可以用尾数0和指数0表示,如图2-6所示。

2.6.1 IEEE浮点数
一个32位IEEE 754单精度浮点数可以被表示为下面的二进制位串:
S EEEEEEEE 1.MMMMMMMMMMMMMMMMMMMMMMM
这里S为符号位,指明这个数是正数还是负数;E为8位偏置指数,指出了小数点的位置;M是23位小数尾数。细数这个数,我们会发现它有33位而不是32位,这是因为当这个数被保存在存储器中时,尾数最前的那个1被省掉了。只有用M表示的尾数的小数部分才会被存入存储器中(后面将很快介绍这样做的原因)。图2-7描述了32位浮点数的结构。
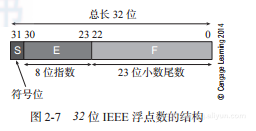
S位为符号位,决定了数的符号。若S = 0,该数为正数,若S = 1,则该数为负。指数E将浮点数的尾数扩大或缩小2的E次方倍,并且它的偏置值为127。例如浮点数+1.11001…0×212的指数为12 + 127 = 13910 = 100010112。
IEEE浮点数的尾数总是规格化的,其值在1.0000…00至1.1111…11之间,除非这个浮点数是0,此时尾数为0.000…00。由于尾数总是规格化的,且它的最高位总是1,因此将尾数存入存储器时没有必要保存最高位的1。所以,一个非0的IEEE 754浮点数可被定义为:
X = -1S × 2E-B × 1·F
式中:
S = 符号位;0 = 正尾数;1 = 负尾数;E = 偏置量为B的指数;F = 尾数的小数部分(注意实际尾数为1·F,有个隐含的1)
前面已经提到,浮点数0应被表示为S = 0,E = 0,M = 0(即浮点数0用全0表示)。
IEEE浮点数被称为字典序的,因为无论两个数是被当作浮点数还是有符号整数,它们的大小顺序都是相同的。这一特性意味着人们可以用简单的逻辑电路比较两个浮点数的大小,电路的复杂度与浮点表示的复杂度无关。
请考虑下面的例子:如何将一个32位IEEE单精度浮点数X解压缩为一个符号位、一个偏置指数和一个尾数。X = 11000001100110011000000000000000。解压缩这3个字段得到
S = 1,E = 10000011,且F = .00110011000000000000000
为了得到实际的尾数,当解压缩尾数时我们会在所保存的尾数的小数部分之前增加一位,得到1. 00110011000000000000000。因此这个数等于
-1.00110011000000000000000×210000011-01111111 = -1. 00110011000000000000000×24 = -10011.0011。
- IEEE浮点数格式
ANSI/IEEE 754-1985标准定义了基本的和扩展的浮点数格式,以及一组数量有限的算术运算的规则(加、减、乘、除、平方根、求余和比较)。
非数(Not a Number, NaN)是IEEE 754标准的一个重要概念。NaN是IEEE 754标准提供的一个专门符号,代表IEEE 754标准格式所不能表示的数。NaN的使用和定义是与系统相关的,可以用NaN来表示所需要表达的任何信息。
IEEE 754标准定义了3种浮点数格式:单精度、双精度和四精度(见表2-7)。在32位IEEE 754单精度浮点数格式中,最大指数Emax为+127,最小指数Emin为-126,并不是我们所想的+128~-127。Emin-1(即-127)用来表示浮点0,Emax+1用来表示正/负无穷大或NaN数。
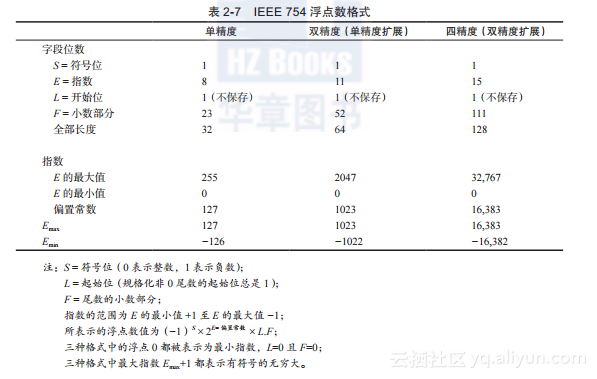
解压缩浮点数时,浮点数指数和尾数的位数都会增加,这种格式被称为扩展格式。通过格式扩展,浮点数的表示范围和精度都增加了。例如,解压缩一个32位浮点数时,增加起始位1可将23位的尾数小数部分扩展到24位,然后尾数被扩展为32位(要么作为一个32位字,要么作为两个16位字)。接下来的所有运算都在32位扩展精度的尾数上进行。扩展格式上的运算完成之后,运算结果按照原先的格式重新压缩并保存在存储器中。
最小指数的绝对值小于最大指数的绝对值,以确保计算最小数的倒数时不会产生上溢。当然,反过来就意味着最大数的倒数会产生下溢。不过下溢带来的问题没有上溢那么严重。
图2-8描述了IEEE单精度浮点数格式。指数E=0和E=255等特例分别被用于表示浮点0、非规格化小数、正或负无穷大,以及NaN数等。
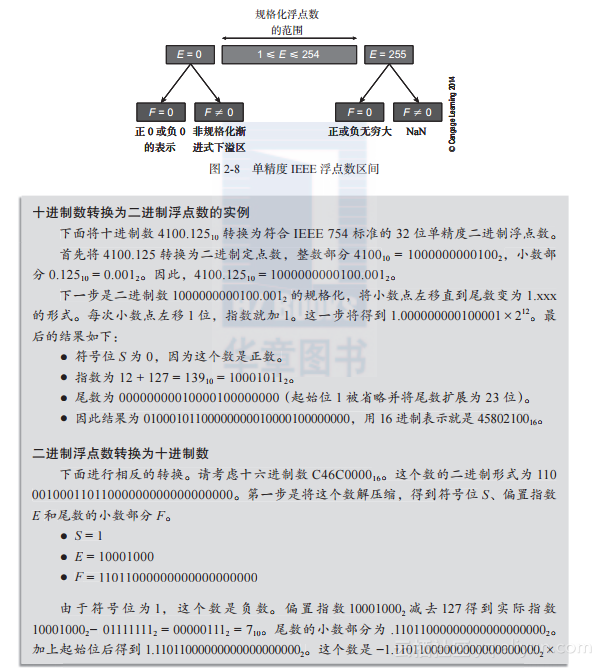

- IEEE浮点数的特点
首先来看看浮点数的一些不明显的特点。请考虑两个浮点数F1和F2的差,这两个数只有最低位不同;即
d=F2-F1=e2x1. f2-e1×1. f1=2e2-b×1. f2-2e2-b×1. f1=2e-b×0.000,..,1
这两个数的差是2-p×2e-b,这里p是尾数的位数,b是指数e的偏置常数。当指数e的值很大时,两个连续的浮点数的差也很大;而当b的值很小时,差也很小。
浮点数的另一个特点与接近0时的情形有关。图2-9描述了一个指数为2位,尾数为2位的浮点数系统。浮点数0表示为00 000。下一个规格化的正数表示为00 100(即2-b×1.00,这里b为偏置常数)。
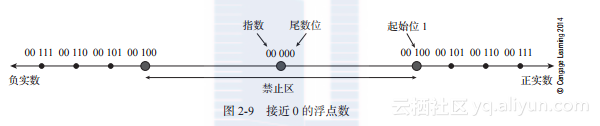
图2-9说明,浮点数0附近有一块禁止区,其中的浮点数都是非规格化的,因此无法被表示为IEEE标准格式。这个数的指数和起始位都是0的区域,也可用来表示浮点数。不过,这些数都是非规格化的,其精度比规格化数的精度低,会导致渐进式下溢。


相关文章:

javascript/dom:原生的JS写选项卡方法
来源:http://www.jb51.net/article/30108.htm <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd"> <html xmlns"http://www.w3.org/1999/xhtml"><head><meta http-…
CSDN 星城大巡礼,长沙“科技之星”年度企业评选正式开启
2020年,长沙市委主要领导发出“软件产业再出发”的号召,颁布了软件三年行动计划。今年5月,CSDN 作为专业的 IT 社区,与长沙高新区签约,将全国总部落户长沙,这一战略决策,让CSDN与长沙的联结进一…

Linux下用C获取当前系统时间
#include <time.h> time_t time(time_t calptr); 返回的是日历时间,即国际标准时间公元1970年1月1日00 : 00 : 00以来经过的秒数。然后再调用 char *ctime(const time_t calptr) ; 转化为字符串表示 #include <stdio.h> #inc…

Java程序猿的JavaScript学习笔记(12——jQuery-扩展选择器)
计划按例如以下顺序完毕这篇笔记:Java程序猿的JavaScript学习笔记(1——理念) Java程序猿的JavaScript学习笔记(2——属性复制和继承) Java程序猿的JavaScript学习笔记(3——this/call/apply) J…
关于动态规划,你想知道的都在这里了!
作者 | Your DevOps Guy翻译| 火火酱~,责编 | 晋兆雨出品 | AI科技大本营头图 | 付费下载于视觉中国什么是动态规划?它又有什么重要的呢?在本文中,我将介绍由Richard Bellman在20世纪50年代提出的动态规划(dynamic pro…

Tcpdump命令的使用与示例——linux下的网络分析
顾名思义,TcpDump可以将网络中传送的数据包的“头”完全截获下来提供分析。它支持针对网络层、协议、主机、网络或端口的过滤,并提供and、or、not等逻辑语句来帮助你去掉无用的信息。tcpdump就是一种免费的网络分析工具,尤其其提供了源代码&a…

document.getElementById与getElementByName的区别
document.getElementById( "id_Number ") 得到的是单个元素 document.getElementsByName( "name ") 得到的是数组 转载于:https://www.cnblogs.com/qiuh/archive/2013/04/16/3023596.html
HDU 3507:Print Article
HDU 3507:Print Article 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid3507 题目大意:给定$n$,$m$,输出序列$n$个数,每连续输出代价为连续输出的数字和的平方加上$m$. 斜率优化DP 定义$sum_{pq}\su…

Linux wait函数解析
进程一旦调用了 wait,就 立即阻塞自己,由wait自动分析是否当前进程的某个子进程已经退出,如果让它找到了这样一个已经变成僵尸的子进程,wait 就会收集这个子进程的信息, 并把它彻底销毁后返回;如果没有找到…
Python多阶段框架实现虚拟试衣间,超逼真!
作者 | 李秋键 责编 | 晋兆雨 头图 | CSDN下载自视觉中国 任意姿态下的虚拟试衣因其巨大的应用潜力而引起了人们的广泛关注。然而,现有的方法在将新颖的服装和姿势贴合到一个人身上的同时,很难保留服装纹理和面部特征(面孔、毛发)中的细节。故在论文《Do…

百度重置页面自动跳转脚本
大家都知道的原因,百度现在不允许其它搜索引擎直接进入的它旗下的所有站点,在痛苦的被增加了很多点击后写了这个自动跳转的脚本。 原来不只搜索引擎,其它网站的链接也被搞了,nnd,诅咒百度。 使用方法:用xxx…

MYSQL 数据库迁移 ***
1. 导出数据库数据mysqldump -uroot -p webCompile > webCompileOut.sql其中:root 是账户名webCompile 是需要导出的数据库名称webCompileOut.sql 存储导出的数据2. 将导出SecureCRT sz【下载】的数据webCompileOut.sql放到你的目标机器…

exec函数族的使用
调用shell脚本命令:execlp("sh","sh","filename",(char*)0);exec用被执行的程序完全替换调用它的程序的影像。fork创建一个新的进程就产生了一个新的PID,exec启动一个新程序,替换原有的进程,因此这…

全球首个突破200种语言互译的翻译引擎,百度翻译打破世界沟通壁垒
机器翻译作为人工智能关键技术之一,正日益成为企业智能化升级的重要应用场景。12月1日,百度大脑开放日举办了以“机器翻译 沟通全世界”为主题的专场活动。 IDC 中国副总裁兼首席分析师武连峰、百度 AI 技术生态部总经理刘倩、百度人工智能技术委员会主席…
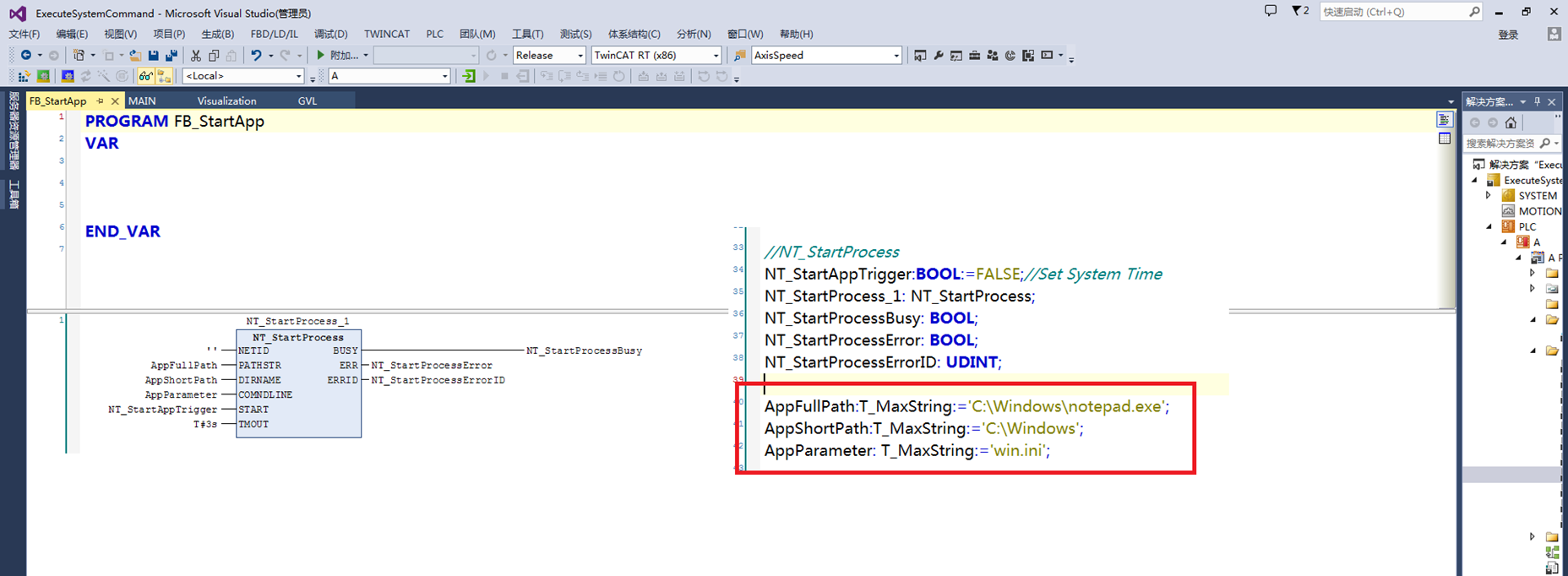
倍福TwinCAT(贝福Beckhoff)基础教程5.1 TwinCAT-2 运行可执行文件
个人认为这条命令做的参数比较混乱,PATHSTR是指可执行文件路径最终文件名,DIRNAME是指可执行文件路径,最后COMNDLINE可有可无,是指带参数运行启动的文件 测试可以正常运行

Linux系统的大小端模式
大端模式所谓的大端模式,是指数据的低位(就是权值较小的后面那几位)保存在内存的高地址中,而数据的高位,保存在内存的低地址中,这样的存储模式有点儿类似于把数据当作字符串顺序处理:地址由小向…
CSDN插件限时内测,新用户抢永久免费去广告特权!
经过程序猿哥哥们和产品小姐姐马不停蹄的疯狂加班,CSDN 官方出品的PC浏览器插件–开发者助手 终于正式上线啦!一键万能操作,新标签页极简个性,让你的浏览器更酷更高效!还有超多实用彩蛋功能等你来解锁!现在…

你必须知道的.net学习总结
着几天在看《你必须知道的.net》,这次看书和以往不同,以前是把自己喜欢的章节看了。但是这次决定把一本书详细的看看。 在第一章第一节中主要讲的是“对象”,我想每一个程序员都对,“对象”有理解。 我来说说书中所说的对象吧。。 我只是把认…

Mybatis 基本配置, 面向接口
< 一 > 主配置文件 <?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE configuration PUBLIC "-//mybatis.org//DTD Config 3.0//EN" "http://mybatis.org/dtd/mybatis-3-config.dtd"> <configuration><…

据说看完这21个故事的人,30岁前都成了亿万富翁。你是下一个吗?
1.甲去买烟,烟29元,但他没火柴,跟店员说:“顺便送一盒火柴吧。”店员没给。 乙去买烟,烟29元,他也没火柴,跟店员说:“便宜一毛吧。”最后,他用这一毛买一盒火柴。 这是…

助力视障人士,微软等公司捐赠首批AI有声内容
12月2日,微软与周迅AI语音红丹丹公益项目发起人鹿音苑文化传播公司,以及来自微软及各界的150名余志愿者,将创作的首批人工智能有声内容,包括鲁迅、老舍、萧红、朱自清等作家的一系列经典作品、红丹丹文化期刊,正式捐赠…

能和LoadRunner匹敌的VS2010/2012Web负载测试
VS自带的Web负载测试真的很大程度上能和专业的loadrunner媲美(只是Web方面),上个report图吧(如何实现,请往下拉): 看,能探测一堆的计数器(上面红色打叉的是代表超过了基线…

设置编码格式为utf8
response.setCharacterEncoding("UTF-8"); 在Servlet2.3中是不行的,至少要2.4版本才可以,如果低于2.4版本,可以用如下办法: response.setContentType("text/html;charsetUTF-8"); pageEncoding"UTF-8&qu…
Linux 命令集锦
linux下查看监听端口对应的进程 # lsof -i:9000 # lsof -Pnl M -i4# lsof -i | grep 9054 如果退格键变成了:"^h"。 终端连接unix删除退格键,按住CTL键同时按deleteLinux搜索 # find / -name "xxx.conf"查看linux是32位还是64位的命…

mysql (双主,互主)
Master-Master(双主) 1、测试环境 Master/Slave Master1/Slave1 IP 192.168.1.13 192.168.1.10 为了保持干净的环境:两边服务器 rm -rf /var/lib/mysql/* service mysqld re…
熬夜都要看完的 Python 干货!
结合我最近这些年的Python学习、开发经验,发现超90%的人在初学Python时都会遇到下面这些问题:没经验不知道怎么开始学,应用方向太多了根本不知道该怎么选择!各基础入门看似简单,但一到进阶部分就举步维艰,遇…

Linux下二进制文件安装MySQL
MySQL 下载地址:https://dev.mysql.com/downloads/mysql/ 并按如下方式选择来下载安装包。 1. 设置配置文件/etc/my.cnmore /etc/my.cnf [client] port 3306 socket /tmp/mysql.sockdefault-character-setutf8[mysqld] usermysql port 3306 server_id 1 socket/…

解决远程桌面无法连接问题
如果 出现的提示如下:---------------------------中断远程桌面连接---------------------------客户端无法建立跟远程计算机的连接。导致这个错误的可能的原因是:1) 远程计算机上的远程连接可能没有启用。2) 已超出远程计算机上的连接最大数。3) 建立连接时出现了一…
这些算法在印度农村医疗中发挥极大作用,未来还将发挥哪些作用?
作者 | Apoorva Mandavilli译者 | Jhonny,责编 | Carol来源 | Unitimes在结核病猖獗的印度农村等地方,用于扫描肺部X射线的 AI 技术可能有助于消除这种疾病之苦。印度农村马哈拉施特拉邦的 Chinchpada Mission 医院在世界上一些最偏远和最贫困的角落&…

四层和七层交换技术-loadbalance
1 四层交换技术简介 我们知道,二层交换机是根据第二层数据链路层的MAC地址和通过站表选择路由来完成端到端的数据交换的。三层交换机是直接根据第三层网络层IP地址来完成端到端的数据交换的。四 层交换机不仅可以完成端到端交换,还能根据端口主机的应用特…
