当前位置：首页 > 编程日记 > 正文

深度学习与计算机视觉系列(9)_串一串神经网络之动手实现小例子

编程日记 2024-11-14 16:20:00

深度学习与计算机视觉系列(9)_串一串神经网络之动手实现小例子

作者：寒小阳
时间：2016年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/50521072
声明：版权所有，转载请联系作者并注明出处

1.引言

前面8小节，算从神经网络的结构、简单原理、数据准备与处理、神经元选择、损失函数选择等方面把神经网络过了一遍。这个部分我们打算把知识点串一串，动手实现一个简单的2维平面神经网络分类器，去分割平面上的不同类别样本点。为了循序渐进，我们打算先实现一个简单的线性分类器，然后再拓展到非线性的2层神经网络。我们可以看到简单的浅层神经网络，在这个例子上就能够有分割程度远高于线性分类器的效果。

2.样本数据的产生

为了凸显一下神经网络强大的空间分割能力，我们打算产生出一部分对于线性分类器不那么容易分割的样本点，比如说我们生成一份螺旋状分布的样本点，如下：

N = 100 # 每个类中的样本点
D = 2 # 维度
K = 3 # 类别个数 X = np.zeros((N*K,D)) # 样本input y = np.zeros(N*K, dtype='uint8') # 类别标签 for j in xrange(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # 可视化一下我们的样本点 plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)

得到如下的样本分布：

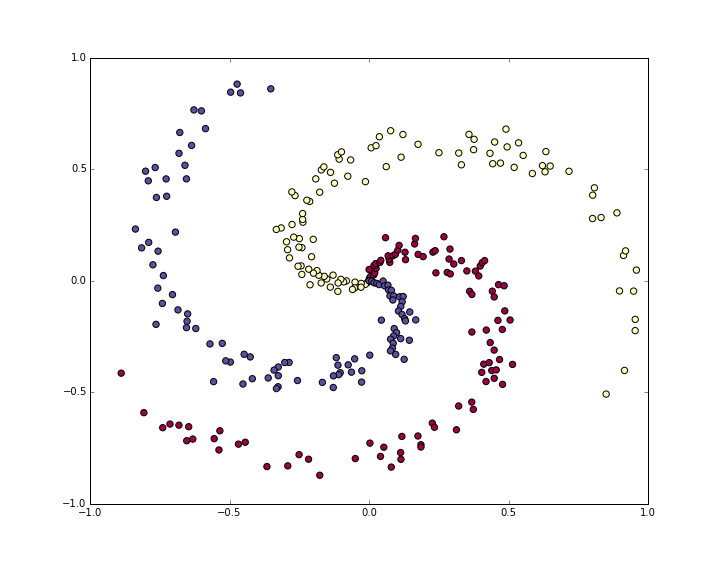
紫色，红色和黄色分布代表不同的3种类别。

一般来说，拿到数据都要做预处理，包括之前提到的去均值和方差归一化。不过我们构造的数据幅度已经在-1到1之间了，所以这里不用做这个操作。

3.使用Softmax线性分类器

3.1 初始化参数

我们先在训练集上用softmax线性分类器试试。如我们在之前的章节提到的，我们这里用的softmax分类器，使用的是一个线性的得分函数/score function，使用的损失函数是交叉熵损失/cross-entropy loss。包含的参数包括得分函数里面用到的权重矩阵W和偏移量b，我们先随机初始化这些参数。

#随机初始化参数
import numpy as np
#D=2表示维度，K=3表示类别数
W = 0.01 * np.random.randn(D,K) b = np.zeros((1,K))

3.2 计算得分

线性的得分函数，将原始的数据映射到得分域非常简单，只是一个直接的矩阵乘法。

#使用得分函数计算得分
scores = np.dot(X, W) + b

在我们给的这个例子中，我们有2个2维点集，所以做完乘法过后，矩阵得分scores其实是一个[300*3]的矩阵，每一行都给出对应3各类别(紫，红，黄)的得分。

3.3 计算损失

然后我们就要开始使用我们的损失函数计算损失了，我们之前也提到过，损失函数计算出来的结果代表着预测结果和真实结果之间的吻合度，我们的目标是最小化这个结果。直观一点理解，我们希望对每个样本而言，对应正确类别的得分高于其他类别的得分，如果满足这个条件，那么损失函数计算的结果是一个比较低的值，如果判定的类别不是正确类别，则结果值会很高。我们之前提到了，softmax分类器里面，使用的损失函数是交叉熵损失。一起回忆一下，假设f是得分向量，那么我们的交叉熵损失是用如下的形式定义的：

L i = - log ⎛⎝ e f y i \sum j e f j ⎞⎠

直观地理解一下上述形式，就是Softmax分类器把类别得分向量f中每个值都看成对应三个类别的log似然概率。因此我们在求每个类别对应概率的时候，使用指数函数还原它，然后归一化。从上面形式里面大家也可以看得出来，得到的值总是在0到1之间的，因此从某种程度上说我们可以把它理解成概率。如果判定类别是错误类别，那么上述公式的结果就会趋于无穷，也就是说损失相当相当大，相反，如果判定类别正确，那么损失就接近

当然，当然，别忘了，完整的损失函数定义，一定会加上正则化项，也就是说，完整的损失L应该有如下的形式：

L = 1 N \sum i L i  data loss + 1 2 λ \sum k \sum l W 2 k , l  regularization loss

好，我们实现以下，根据上面计算得到的得分scores，我们计算以下各个类别上的概率：

# 用指数函数还原
exp_scores = np.exp(scores)
# 归一化
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

在我们的例子中，我们最后得到了一个[300*3]的概率矩阵prob，其中每一行都包含属于3个类别的概率。然后我们就可以计算完整的互熵损失了：

#计算log概率和互熵损失
corect_logprobs = -np.log(probs[range(num_examples),y])
data_loss = np.sum(corect_logprobs)/num_examples
#加上正则化项
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss

正则化强度

3.4 计算梯度与梯度回传

我们能够用损失函数评估预测值与真实值之间的差距，下一步要做的事情自然是最小化这个值。我们用传统的梯度下降来解决这个问题。多解释一句，梯度下降的过程是：我们先选取一组随机参数作为初始值，然后计算损失函数在这组参数上的梯度(负梯度的方向表明了损失函数减小的方向)，接着我们朝着负梯度的方向迭代和更新参数，不断重复这个过程直至损失函数最小化。为了清楚一点说明这个问题，我们引入一个中间变量

p k = e f k \sum j e f j

我们现在希望知道朝着哪个方向调整权重能够减小损失，也就是说，我们需要计算梯度

\partial L i \partial f k = p k - 1 ( y i = k )

解释一下，公式的最后一个部分表示

我们依旧记probs为所有样本属于各个类别的概率，记dscores为得分上的梯度，我们可以有以下的代码：

dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

我们计算的得分scores = np.dot(X, W)+b，因为上面已经算好了scores的梯度dscores，我们现在可以回传梯度计算W和b了：

dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
#得记着正则化梯度哈
dW += reg*W

我们通过矩阵的乘法得到梯度部分，权重W的部分加上了正则化项的梯度。因为我们在设定正则化项的时候用了系数0.5（因为

3.5 参数迭代与更新

在得到所需的所有部分之后，我们就可以进行参数更新了：

#参数迭代更新
W += -step_size * dW
b += -step_size * db

3.6 大杂合：训练SoftMax分类器

#代码部分组一起，训练线性分类器#随机初始化参数
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))#需要自己敲定的步长和正则化系数 step_size = 1e-0 reg = 1e-3 #正则化系数 #梯度下降迭代循环 num_examples = X.shape[0] for i in xrange(200): # 计算类别得分, 结果矩阵为[N x K] scores = np.dot(X, W) + b # 计算类别概率 exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] # 计算损失loss(包括互熵损失和正则化部分) corect_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(corect_logprobs)/num_examples reg_loss = 0.5*reg*np.sum(W*W) loss = data_loss + reg_loss if i % 10 == 0: print "iteration %d: loss %f" % (i, loss) # 计算得分上的梯度 dscores = probs dscores[range(num_examples),y] -= 1 dscores /= num_examples # 计算和回传梯度 dW = np.dot(X.T, dscores) db = np.sum(dscores, axis=0, keepdims=True) dW += reg*W # 正则化梯度 #参数更新 W += -step_size * dW b += -step_size * db

得到结果：

iteration 0: loss 1.096956
iteration 10: loss 0.917265
iteration 20: loss 0.851503 iteration 30: loss 0.822336 iteration 40: loss 0.807586 iteration 50: loss 0.799448 iteration 60: loss 0.794681 iteration 70: loss 0.791764 iteration 80: loss 0.789920 iteration 90: loss 0.788726 iteration 100: loss 0.787938 iteration 110: loss 0.787409 iteration 120: loss 0.787049 iteration 130: loss 0.786803 iteration 140: loss 0.786633 iteration 150: loss 0.786514 iteration 160: loss 0.786431 iteration 170: loss 0.786373 iteration 180: loss 0.786331 iteration 190: loss 0.786302

190次循环之后，结果大致收敛了。我们评估一下准确度：

#评估准确度
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

输出结果为49%。不太好，对吧？实际上也是可理解的，你想想，一份螺旋形的数据，你偏执地要用一个线性分类器去分割，不管怎么调整这个线性分类器，都非常非常困难。我们可视化一下数据看看决策边界(decision boundaries)：

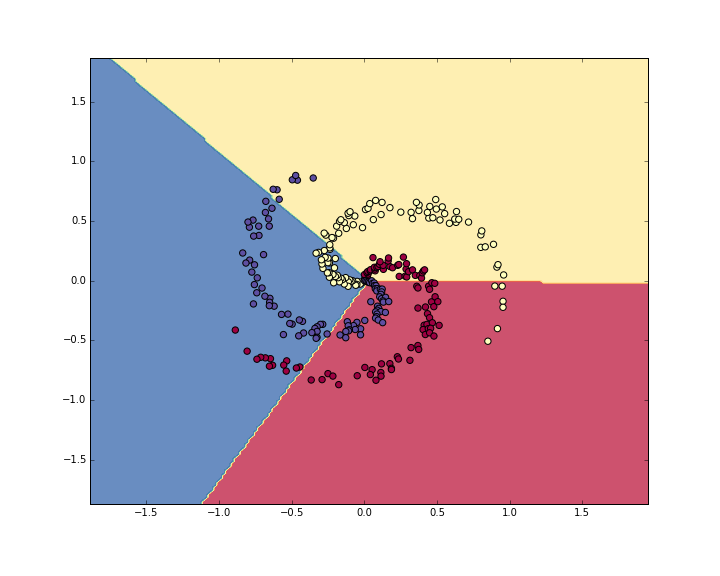
4.使用神经网络分类

从刚才的例子里可以看出，一个线性分类器，在现在的数据集上效果并不好。我们知道神经网络可以做非线性的分割，那我们就试试神经网络，看看会不会有更好的效果。对于这样一个简单问题，我们用单隐藏层的神经网络就可以了，这样一个神经网络我们需要2层的权重和偏移量：

# 初始化参数
h = 100 # 隐层大小(神经元个数)
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h)) W2 = 0.01 * np.random.randn(h,K) b2 = np.zeros((1,K))

然后前向计算的过程也稍有一些变化：

#2层神经网络的前向计算
hidden_layer = np.maximum(0, np.dot(X, W) + b) # 用的 ReLU单元
scores = np.dot(hidden_layer, W2) + b2

注意到这里，和之前线性分类器中的得分计算相比，多了一行代码计算，我们首先计算第一层神经网络结果，然后作为第二层的输入，计算最后的结果。哦，对了，代码里大家也看的出来，我们这里使用的是ReLU神经单元。

其他的东西都没太大变化。我们依旧按照之前的方式去计算loss，然后计算梯度dscores。不过反向回传梯度的过程形式上也有一些小小的变化。我们看下面的代码，可能觉得和Softmax分类器里面看到的基本一样，但注意到我们用hidden_layer替换掉了之前的X:

# 梯度回传与反向传播
# 对W2和b2的第一次计算
dW2 = np.dot(hidden_layer.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)

恩，并没有完事啊，因为hidden_layer本身是一个包含其他参数和数据的函数，我们得计算一下它的梯度：

dhidden = np.dot(dscores, W2.T)

现在我们有隐层输出的梯度了，下一步我们要反向传播到ReLU神经元了。不过这个计算非常简单，因为

#梯度回传经过ReLU
dhidden[hidden_layer <= 0] = 0

终于，翻山越岭，回到第一层，拿到总的权重和偏移量的梯度：

dW = np.dot(X.T, dhidden)
db = np.sum(dhidden, axis=0, keepdims=True)

来，来，来。组一组，我们把整个神经网络的过程串起来：

# 随机初始化参数
h = 100 # 隐层大小
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h)) W2 = 0.01 * np.random.randn(h,K) b2 = np.zeros((1,K)) # 手动敲定的几个参数 step_size = 1e-0 reg = 1e-3 # 正则化参数 # 梯度迭代与循环 num_examples = X.shape[0] for i in xrange(10000): hidden_layer = np.maximum(0, np.dot(X, W) + b) #使用的ReLU神经元 scores = np.dot(hidden_layer, W2) + b2 # 计算类别概率 exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] # 计算互熵损失与正则化项 corect_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(corect_logprobs)/num_examples reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2) loss = data_loss + reg_loss if i % 1000 == 0: print "iteration %d: loss %f" % (i, loss) # 计算梯度 dscores = probs dscores[range(num_examples),y] -= 1 dscores /= num_examples # 梯度回传 dW2 = np.dot(hidden_layer.T, dscores) db2 = np.sum(dscores, axis=0, keepdims=True) dhidden = np.dot(dscores, W2.T) dhidden[hidden_layer <= 0] = 0 # 拿到最后W,b上的梯度 dW = np.dot(X.T, dhidden) db = np.sum(dhidden, axis=0, keepdims=True) # 加上正则化梯度部分 dW2 += reg * W2 dW += reg * W # 参数迭代与更新 W += -step_size * dW b += -step_size * db W2 += -step_size * dW2 b2 += -step_size * db2

输出结果：

iteration 0: loss 1.098744
iteration 1000: loss 0.294946
iteration 2000: loss 0.259301 iteration 3000: loss 0.248310 iteration 4000: loss 0.246170 iteration 5000: loss 0.245649 iteration 6000: loss 0.245491 iteration 7000: loss 0.245400 iteration 8000: loss 0.245335 iteration 9000: loss 0.245292

现在的训练准确度为：

#计算分类准确度
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

你猜怎么着，准确度为98%，我们可视化一下数据和现在的决策边界：

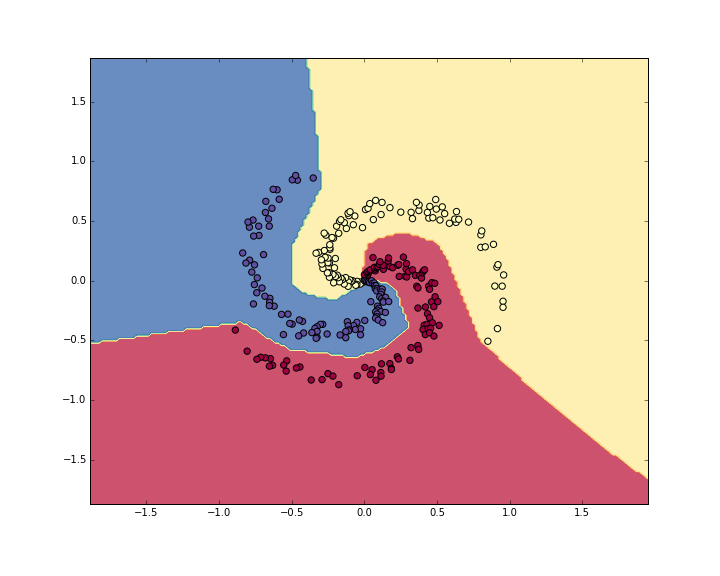
看起来效果比之前好多了，这充分地印证了我们在手把手入门神经网络系列(1)_从初等数学的角度初探神经网络中提到的，神经网络对于空间强大的分割能力，对于非线性的不规则图形，能有很强的划分区域和区分类别能力。

参考资料与原文

cs231n 神经网络小例子

https://www.dkcj.cn/info/27492.html