赠书 | 算力时代，用 Python 来快速解决复杂问题

Python作为一种编程语言，拥有简洁、高效的表达能力。与此同时，Python语言环境中还配备各种软件库，即模块。结合实际问题，选择适当的模块，便可生成简单、快速、正确的程序。

书中列举了一些数值计算的简单例题，以便说明Python数值计算程序的基本组成方法。并在此基础上，介绍利用Python模块构成数值计算程序的方法基础。

Python数值计算程序

首先，我们思考一下运用Python原有功能进行数值计算的情景，这里所说的“Python原有功能”指不使用特殊模块，仅利用Python单体语言功能编辑程序的意思。

举个简单数值计算的例子，如制作一个求某数平方根的程序。与多数编程语言一样，Python中也含有求平方根的程序库。不过，在这里我们特意不使用它，而采用数值计算的算法，尝试求平方根。

求数a的平方根，即相当于求下面2次方程式中x的值。

x²- a=0

解该方程式的方法虽然有很多，这里我们将考虑采用2分法（bip method）求解。以下就是2分法的解题思路。

现假设方程的一个解为x1，在x1的周围，考虑一下函数f(x)=x²-a的值是如何分布的。如，设a=2，在x1＞0的一侧，函数f(x)如图1.1所示。

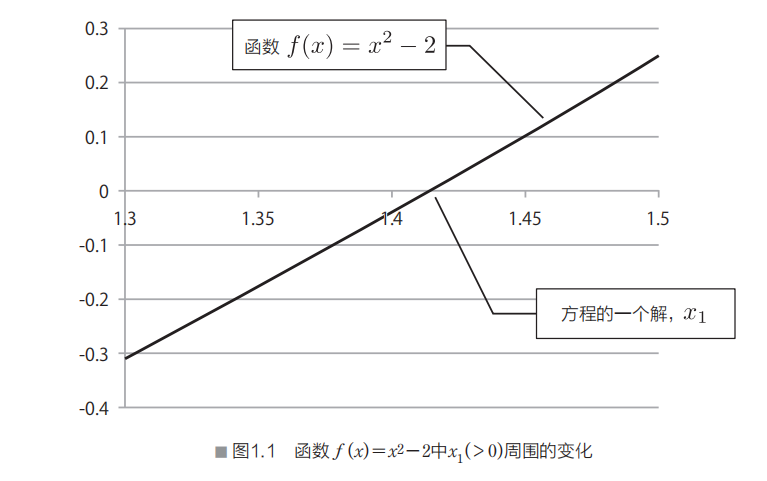
图1.1中，求函数f(x)与x轴的交点，也就是求f(x)=0的解x1。在2分法中，求交点值，首先，要确定该值所在区间的上限和下限。在图1.1的例子当中，选取合适的上限值f(xp)＞0的xp，以及下限值f(xn)＜0的xn。解x1则应该存在于xn与xp之间。将此区间设为初始值，通过逐渐缩小区间来求x1。

例如，从图1.1中，现设xn=1.3，xp=1.5，则可知解x1存在于1.3到1.5之间的区间（图1.2）。

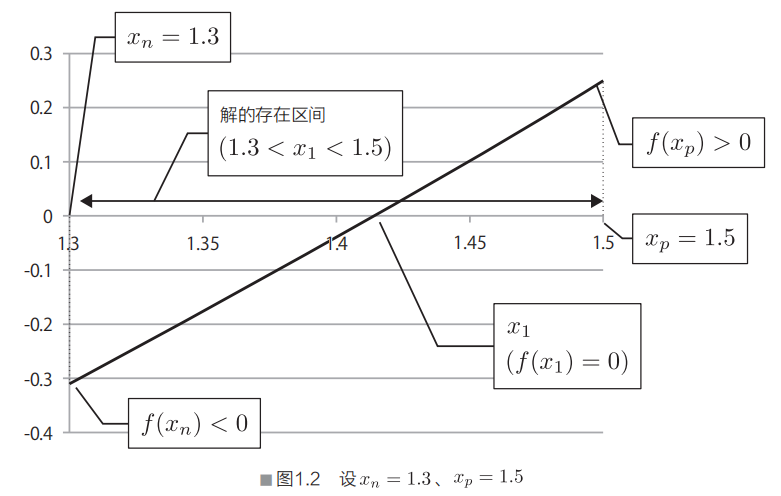
根据2分法，接下来需要求出上限xp和下限xn的中点值。如下可简单算出：

(xp+xn)/2

然后求出所得中点值对应的函数f(x)的值。进而便可计算出该值的正负。

f((xp+xn)/2)

若中点值对应的函数值f((xp+xn)/2)为正，则将该中点值新设为上限值xp。反之，函数值为负，则将该中点值新设为下限值xn。在现在的例子中，

f((1.5+1.3)/2)=f(1.4)=﹣0.04＜0

故可将下限xn的值更新为中点值1.4。因此，可得，解的区间也从初始状态缩小至1.4到1.5之间（图1.3）。

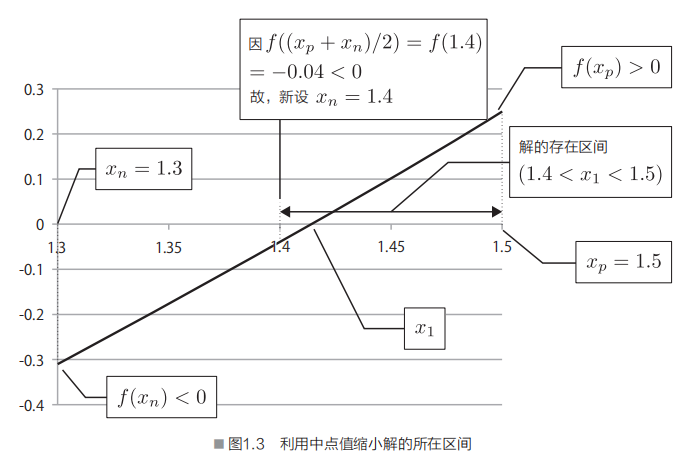
重复上述操作后，如表1.1所示，解的所在区间便逐渐缩小。

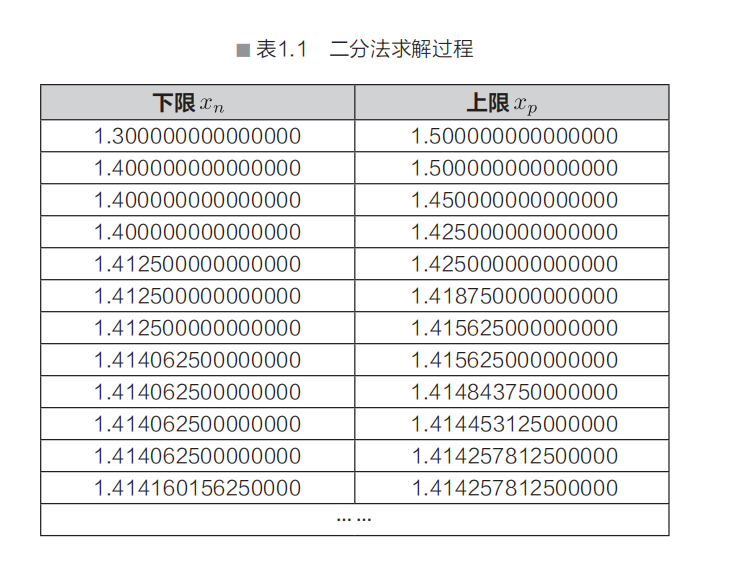在实际计算过程中，通过运用适当的条件，终止重复操作，从而得以求解。

那么，现在我们尝试把2分法的步骤做成Python程序来进行表达。在版本2的Python 2和版本3的Python 3当中，Python的程式语法等有所不同。本书决定使用最新的Python 3。

将2分法的算法翻译成Python代码后，其程式的中心部分可见下述内容。

# 循环处理

while (xp - xn ) * (xp - xn ) >LIMIT:       #满足终止条件前循环

xmid =  (xp + xn ) / 2             #计算新的中点值

if f(xmid) > 0:                    #中点函数值为正

xp=xmid                    #更新xp

else:                          #中点函数值为负

xn=xmid                    #更新xn

这里的变量xp对应xp，变量xn对应xn。另外，xmid代表新的中点值，函数f()返回的是f(x)=x²-2的值。常数LIMIT设置的值用来判断终止重复。

以上述Python代码为中心，对函数f()的定义以及变量进行初始设定后，便可实现2分法的程序bisec.py。见列表1.1的bisec.py。

列表1.1  bisec.py程序：

 1:# -*- coding: utf-8 -*-2:"""
■ 表1.1　二分法求解过程
下限 　　 上限 　　
1.300000000000000 1.500000000000000
1.400000000000000 1.500000000000000
1.400000000000000 1.450000000000000
1.400000000000000 1.425000000000000
1.412500000000000 1.425000000000000
1.412500000000000 1.418750000000000
1.412500000000000 1.415625000000000
1.414062500000000 1.415625000000000
1.414062500000000 1.414843750000000
1.414062500000000 1.414453125000000
1.414062500000000 1.414257812500000
1.414160156250000 1.414257812500000
……
第1章　Python数值计算
133:bisec.py程序4:二分法解方程式的程序5:使用方法　c:\>python bisec.py6:"""7:# 全局变量8:a = 2 # f(x)=x*x-a9:LIMIT = 1e-20 # 终止条件
10:
11:# 分包函数定义
12:# f()函数
13:def f(x):
14: """函数值的计算"""
15: return x * x - a
16:# f()函数结束
17:
18:# 主执行部分
19:# 初始设置
20:xp = float(input("请输入xp:"))
21:xn = float(input("请输入xn:"))
22:
23:# 循环处理
24:while (xp - xn) * (xp - xn) > LIMIT: # 满足终止条件前循环
25: xmid = (xp + xn) / 2 # 计算新的中点值
26: if f(xmid) > 0: # 中点函数值为正
27: xp = xmid # 更新xp
28: else: # 中点函数值为负
29: xn = xmid # 更新xn
30: print("{:.15f} {:.15f}".format(xn, xp))
31:# bisec.py结束

bisec.py的执行结果见执行例1.1。

执行例1.1  bisec.py的执行结果：

C:\Users\odaka\Documents\ch1>python bisec.py
请输入xp:1.5
请输入xn:1.3
1.400000000000000 1.500000000000000
1.400000000000000 1.450000000000000
1.400000000000000 1.425000000000000
扫码看视频
1.1　Python数值计算程序的结构
14
1.412500000000000 1.425000000000000（下面持续输出）
1.414213562197983 1.414213562384248
1.414213562291116 1.414213562384248
C:\Users\odaka\Documents\ch1>

Python模块的应用

在上一节，为求平方根，特意使用了2分法的算法进行求解。这在学习2分法算法的意义上，很有必要，但若考虑到编程的工序，并非称得上简易方法。实际上，很多编程语言都具备求平方根的程序库。这一点，Python也一样。

在Python里，求正的平方根要引入math模块。如下所示，使用math模块，便可简单地求出x的正平方根√x。

math.sqrt(x)

利用math.sqrt()，求正平方根的程序sqrt.py见列表1.2。另，执行的例子见执行例1.2。

列表1.2  sqrt.py程序

 1:# -*- coding: utf-8 -*-2:"""3:sqrt.py程序4:利用math模块求平方根5:使用方法　c:\>python sqrt.py6:"""7:# 引入模块8:import math9:
10:# 主执行部分
11:# 输入
12:x = float(input("输入希望求正平方根的值:"))
13:# 输出
14:print("sqrt(", x, ")=", math.sqrt(x))
15:# sqrt.py结束
C:\Users\odaka\Documents\ch1>python sqrt.py
输入希望求正平方根的值:2
sqrt( 2.0 )= 1.4142135623730951
C:\Users\odaka\Documents\ch1>python sqrt.py
输入希望求正平方根的值:3
sqrt( 3.0 )= 1.7320508075688772
C:\Users\odaka\Documents\ch1>

Python不仅配有求平方根的模块，还备有可以解方程式的模块。在列表1.3中的solve.py程序中，只要描述出方程式，即可实现求解。solve.py使用sympy模块。在本节最后，会对包含sympy模块在内的Python模块的安装方法进行说明。

列表1.3  solve.py程序

 1:# -*- coding: utf-8 -*-2:"""3:solve.py程序4:利用sympy模块解方程式5:有点复杂的方程式例子6:使用方法　c:\>python solve.py 7:"""8:# 引入模块9:from sympy import *
10:
11:# 主执行部分
12:var("x") # 使用变量x
13:equation = Eq(x**3 + 2 * x**2 - 5 * x - 6, 0) # 列方程式
14:answer = solve(equation) # 解方程式
15:print(answer) # 输出结果
16:# solve.py结束

下面内容即为solve.py程序中设定方程式并求解的过程。

12: var(”x”)                               # 利用变量x

13: equation = Eq(x**3 + 2*x**2 - 5*x - 6, 0)    # 列方程式

14: answer = solve(equation)                # 解方程式

15:print(answer)                          # 输出结果

上述内容中，最初在第12行将x设为方程式的变量，在第13行列出了以下方程式。

x³+2x²-5x-6=0

求解该方程式，如下面第14行内容，仅仅使用了solve()给出命令而已。

14: answer = solve(equation)                # 解方程式

其结果便输出到第15行。

15:print(answer)                          # 输出结果

执行例1.3展示了solve.py程序的执行结果。该3次方程式的解如下分别为：

x= -3，-1，2

执行例1.3  solve.py程序的执行结果

C:\Users\odaka\Documents\ch1>python solve.py
[-3, -1, 2]
C:\Users\odaka\Documents\ch1>

小结

在Python里，可以使用的模块除有这里介绍的模块，还有很多方便且高效的模块。后续会酌情介绍一些绘图，行列式计算，微积分等模块。

此外，为了使用这些模块，需要在Python的基础语言系统上追加安装合适的模块。如，列表1.3的solve.py程序，会用到sympy这个模块，为此，需要安装sympy模块。

这种情况也可以单独安装个别模块。但利用Anaconda系统的话，可以打包安装Python基础系统以及各种模块。可从以下URL使用Anaconda。

https://www.anaconda.com/download/

以上链接除可安装本书的使用对象Python3之外，还可选择安装Python2。另外，支持的操作系统可选择Windows，Linux，以及macOS，结合使用环境进行选择。

本文摘编自《Python数值计算与模拟》，经出版方授权发布。

内容简介：本书从传统的数值计算技术到先进的多智能体模拟基础，均边展示Python程序，边对其进行了具体讲解。第1章：运用Python进行数值计算时普遍存在的注意点。第2章和第3章中：运用微分方程式表示的物理现象模拟。第4章：利用元胞自动机的模拟。第5章：利用随机数进行模拟。第6章：多智能体模拟框架。

作者简介：小高知宏，1983年早稻田大学理工学部毕业；1990年早稻田大学研究生院理工学研究科毕业，获工学博士九州大学医学部附属医院助手；1993年福井大学工学部信息工学科副教授；1999年福井大学工学部智能系统工学科副教授。

对于Python数值计算，你有哪些见解呢？

#欢迎来评论区讨论#

AI科技大本营 将选出三名优质留言

携手【中青雄狮出版社】送出

《Python数值计算与模拟》一本

截至5月14日14:00点

更多精彩推荐
☞听完姚期智的一句“嘟囔”，他开始第二次创业☞AI 3D 传感器市场竞争白热化，中国掌握自主可控核心技术时不我待！☞小心！你家的 IoT 设备可能已成为僵尸网络“肉鸡”☞换脸火了，我用 python 快速入门生成模型点分享点收藏点点赞点在看