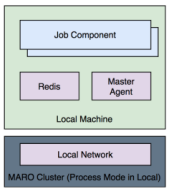
两条路不能有重边,既每条边的容量是1。求流量为2的最小费用即可。


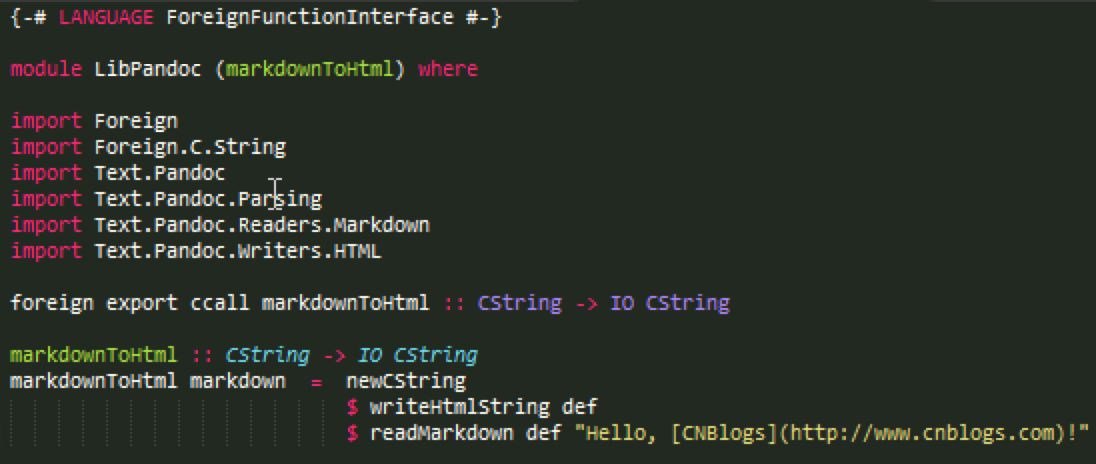
//#pragma comment(linker, "/STACK:1024000000,1024000000") #include<cstdio> #include<cstring> #include<cstdlib> #include<algorithm> #include<iostream> #include<sstream> #include<cmath> #include<climits> #include<string> #include<map> #include<queue> #include<vector> #include<stack> #include<set> using namespace std; typedef long long ll; typedef unsigned long long ull; typedef pair<int,int> pii; #define pb(a) push(a) #define INF 0x1f1f1f1f #define lson idx<<1,l,mid #define rson idx<<1|1,mid+1,r #define PI 3.1415926535898 template<class T> T min(const T& a,const T& b,const T& c) {return min(min(a,b),min(a,c)); } template<class T> T max(const T& a,const T& b,const T& c) {return max(max(a,b),max(a,c)); } void debug() { #ifdef ONLINE_JUDGE #elsefreopen("data.in","r",stdin);// freopen("d:\\out1.txt","w",stdout); #endif } int getch() {int ch;while((ch=getchar())!=EOF){if(ch!=' '&&ch!='\n')return ch;}return EOF; }struct Edge {int from,to,cost,cap; }; const int maxn = 3111;vector<int> g[maxn]; vector<Edge> edge; int n,m,s,t; void init() {for(int i = 1; i <= n; i++)g[i].clear();edge.clear(); } void add(int from, int to, int cost, int cap) {edge.push_back((Edge){from, to, cost, cap});g[from].push_back(edge.size() - 1);edge.push_back((Edge){to, from, -cost, 0});g[to].push_back(edge.size() - 1); }int d[maxn]; int inq[maxn]; int road[maxn];int SPFA() {queue<int> q;q.push(s);memset(d, INF, sizeof(d));memset(inq, 0, sizeof(inq));inq[s] = true;d[s] = 0;road[s] = -1;while(!q.empty()){int x = q.front(); q.pop();inq[x] = false;for(int i = 0; i < g[x].size(); i++){Edge &e = edge[g[x][i]];if(e.cap>0 && d[x] + e.cost < d[e.to]){d[e.to] = d[x] + e.cost;road[e.to] = g[x][i];if(!inq[e.to]){inq[e.to] = true;q.push(e.to);}}}}return d[t]; } int max_cost_flow() {int flow = 2;int cost = 0;while(flow){int d = SPFA();int f = flow;for(int e = road[t]; e != -1; e = road[edge[e].from]){Edge &E = edge[e];f = min(f, E.cap);}flow -= f;cost += d * f;for(int e = road[t]; e != -1; e = road[edge[e].from]){edge[e].cap -= f;edge[e^1].cap += f;}}return cost; } int main() {debug();while(scanf("%d%d", &n, &m) != EOF){init();for(int i = 1; i <= m; i++){int from,to,cost;scanf("%d%d%d", &from, &to, &cost);add(from, to, cost, 1);add(to, from, cost, 1);}s=1;t=n;printf("%d\n", max_cost_flow());}return 0; }