Python 解一道江苏 小升初 数学题,如此变态,看不起来谁?

作者:小小明【江湖人称"明佬"】
链接:blog.csdn.net/as604049322/article/details/118388505
注明:本文经过作者小小明授权发布,可戳原文链接关注原文作者!
本文简介
大家好,我是黄同学????
前段时间,我在群里面发布了一道题。没想到明佬用心了,很快记下了,马上就用Python解答出来了。
题目如下:
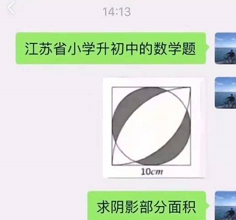
小学题目都这么难,看不起谁呢。今天明佬将尝试通过Python来解题。
首先我们以左下角为原点建立直角坐标系,很快能够知道圆的方程为
两个扇形的方程分别为和的一部分。
上面的方程很容易得到,但要计算出方程表达式还需费一番功夫,所以下面我们打算也让Python来计算。
在解题前,我们会先用Python绘制出如下图像。
结果如下:
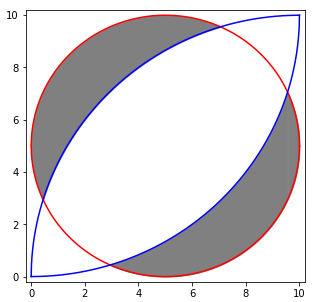
绘图步骤
1. 画圆
首先计算出上半圆和下半的表达式分别为:
from sympy.abc import x, y
import sympyc1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
display(c1)
display(c2)结果如下:
如果想要展开表达式可以进行如下操作:
display(sympy.expand(c1))
display(sympy.expand(c2))结果如下:
直接打印可以看到在Python的表达式:
print(str(c1))
print(str(c2))5 - sqrt(-x*(x - 10))
sqrt(x*(10 - x)) + 5因此利用上述文本,我们可以直接进行numpy的函数求值,下面尝试画个圆试一下:
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=(5, 5))
x = np.linspace(0, 10, 1024)plt.plot(x, eval(str(c1)), color="r")
plt.plot(x, eval(str(c2)), color="r")plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)plt.show()结果如下:
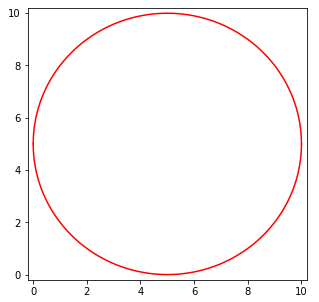
可以看到我们求解的两个表达式可以画出圆形。
下面我们继续来画扇形。
2. 画扇形
两个扇形的方程分别为和的一部分。
首先我们计算上面的扇形的函数公式:
sympy.solve((x-10)**2+y**2 - 10**2, y)结果如下:
[sqrt(x*(20 - x)), -sqrt(-x*(x - 20))]显然上面的扇形的函数公式是正数,可以直接取角标为0的函数公式:
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s1结果如下:
用同样的方法我们再求出下面的扇形:
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
s2结果如下:
然后我们绘制函数图形验证一下:
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy%matplotlib inlinec1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)x = np.linspace(0, 10, 1024)plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), color="r")
plt.plot(x, eval(str(c2)), color="r")plt.plot(x, eval(str(s1)), color="b")
plt.plot(x, eval(str(s2)), color="b")plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)plt.show()结果如下:

3. 绘制阴影
首先我们需要求出四个交点。
先分清几个线各是哪条:
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy%matplotlib inlinec1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)x = np.linspace(0, 10, 1024)plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), label="c1")
plt.plot(x, eval(str(c2)), label="c2")plt.plot(x, eval(str(s1)), label="s1")
plt.plot(x, eval(str(s2)), label="s2")plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()plt.show()结果如下:
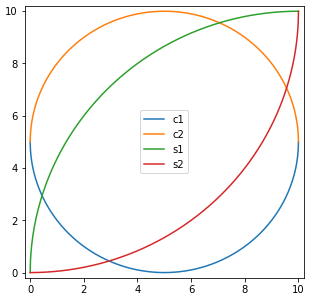
下面分别交出交点:
from sympy.abc import x, yx1, = sympy.solve(c1-s1, x)
x2, = sympy.solve(c1-s2, x)
x3, = sympy.solve(c2-s1, x)
x4, = sympy.solve(c2-s2, x)
x1, x2, x3, x4(15/4 - 5*sqrt(7)/4,25/4 - 5*sqrt(7)/4,5*sqrt(7)/4 + 15/4,5*sqrt(7)/4 + 25/4)根据对称性,我们可以知道四个交点的坐标分别为(x1,x2), (x2,x1), (x3,x4),(x4,x3)
同样可以画图验证一下:
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy%matplotlib inlinec1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1, = sympy.solve(c1-s1, x)
x2, = sympy.solve(c1-s2, x)
x3, = sympy.solve(c2-s1, x)
x4, = sympy.solve(c2-s2, x)x = np.linspace(0, 10, 1024)plt.figure(figsize=(5, 5))
plt.plot(x, eval(str(c1)), label="c1")
plt.plot(x, eval(str(c2)), label="c2")plt.plot(x, eval(str(s1)), label="s1")
plt.plot(x, eval(str(s2)), label="s2")plt.plot([x1, x2, x3, x4], [x2, x1, x4, x3], 'rx')
plt.text(x1, x2+0.1, "p1", ha="center", va="bottom")
plt.text(x2, x1+0.1, "p2", ha="center", va="bottom")
plt.text(x3, x4+0.1, "p3", ha="center", va="bottom")
plt.text(x4, x3+0.1, "p4", ha="center", va="bottom")plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()
plt.show()结果如下:
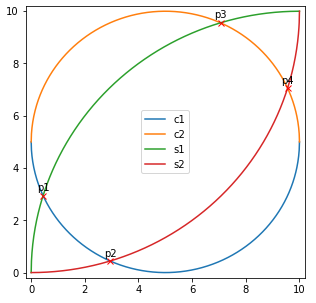
下面开始绘制阴影:
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy%matplotlib inlinec1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()x = np.linspace(0, 10, 1024)
c1, c2, s1, s2 = map(lambda s: eval(str(s)), (c1, c2, s1, s2))plt.figure(figsize=(5, 5))
plt.plot(x, c1, label="c1")
plt.plot(x, c2, label="c2")
plt.plot(x, s1, label="s1")
plt.plot(x, s2, label="s2")plt.fill_between(x[x <= x1], c1[x <= x1], c2[x <= x1], color="grey")
plt.fill_between(x[(x1 < x) & (x <= x3)], s1[(x1 < x) &(x <= x3)], c2[(x1 < x) & (x <= x3)], color="grey")
plt.fill_between(x[(x2 <= x) & (x <= x4)], c1[(x2 <= x) & (x <= x4)], s2[(x2 <= x) & (x <= x4)], color="grey")
plt.fill_between(x[x > x4], c1[x > x4], c2[x > x4], color="grey")plt.plot([x1, x2, x3, x4], [x2, x1, x4, x3], 'rx')plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.legend()
plt.show()结果如下:
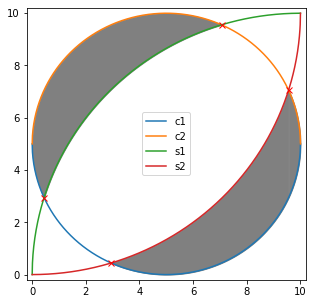
然后再稍微调整一下颜色即可得到文章开头的图像。
4. 绘图完整代码
import numpy as np
from numpy import sqrt
import matplotlib.pyplot as plt
from sympy.abc import x, y
import sympy%matplotlib inlinec1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()x = np.linspace(0, 10, 1024)
c1, c2, s1, s2 = map(lambda s: eval(str(s)), (c1, c2, s1, s2))plt.figure(figsize=(5, 5))
plt.plot(x, c1, label="c1", color="r")
plt.plot(x, c2, label="c2", color="r")
plt.plot(x, s1, label="s1", color="b")
plt.plot(x, s2, label="s2", color="b")plt.fill_between(x[x <= x1], c1[x <= x1], c2[x <= x1], color="grey")
plt.fill_between(x[(x1 < x) & (x <= x3)], s1[(x1 < x) &(x <= x3)], c2[(x1 < x) & (x <= x3)], color="grey")
plt.fill_between(x[(x2 <= x) & (x <= x4)], c1[(x2 <= x) & (x <= x4)], s2[(x2 <= x) & (x <= x4)], color="grey")
plt.fill_between(x[x > x4], c1[x > x4], c2[x > x4], color="grey")plt.xlim(-0.2, 10.2)
plt.ylim(-0.2, 10.2)
plt.show()在完成图像绘制后,我们就可以通过相同的思路求积分得到面积了。
积分求解面积
最终结果完整求解代码:
from sympy.abc import x, y
from sympy import integrate
import sympyc1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0].evalf()
x2 = sympy.solve(c1-s2, x)[0].evalf()
x3 = sympy.solve(c2-s1, x)[0].evalf()
x4 = sympy.solve(c2-s2, x)[0].evalf()r = integrate(c2-c1, (x, 0, x1))+integrate(c2-s1, (x, x1, x3)) + \integrate(s2-c1, (x, x2, x4))+integrate(c2-c1, (x, x4, 10))
r.round(4)结果:29.2763
如果希望得到更加精确的的结果,可以最后再调用evalf方法:
from sympy.abc import x, y
from sympy import integrate
import sympyc1, c2 = sympy.solve((x-5)**2+(y-5)**2 - 5**2, y)
s1, _ = sympy.solve((x-10)**2+y**2 - 10**2, y)
s2, _ = sympy.solve(x**2+(y-10)**2 - 10**2, y)
x1 = sympy.solve(c1-s1, x)[0]
x2 = sympy.solve(c1-s2, x)[0]
x3 = sympy.solve(c2-s1, x)[0]
x4 = sympy.solve(c2-s2, x)[0]r = integrate(c2-c1, (x, 0, x1))+integrate(c2-s1, (x, x1, x3)) + \integrate(s2-c1, (x, x2, x4))+integrate(c2-c1, (x, x4, 10))
r.evalf()
结果:29.2762519060696



往
期
回
顾
资讯
GitHub的AI编程代码漏洞40%
资讯
AI复活她,OpenAI又夺走她
资讯
英伟达用 AI 给自家纪录片配音
转载
人脸识别模型的动手实践!

分享

点收藏

点点赞

点在看
相关文章:
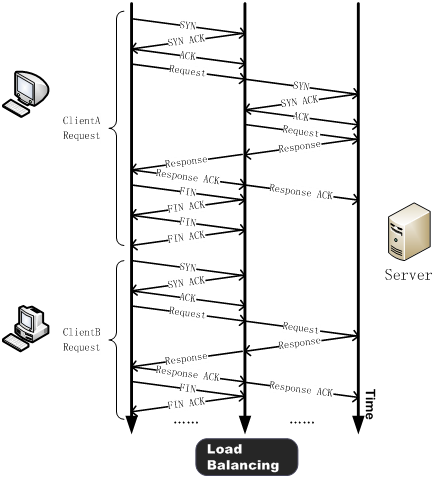
利用负载均衡优化和加速HTTP应用
1.负载均衡技术简介 现代企业信息化应用越来越多的采用B/S应用架构来承载企业的关键业务,因此,确保这些任务的可靠运行就变得日益重要。随着越来越多的企业实施数据集中,应用的扩展性、安全性和可靠性也越来越受到企业的重视。 负载均衡技术通…

查看sqlserver被锁的表以及如何解锁
查看sqlserver被锁的表以及如何解锁查看被锁表:www.2cto.com select request_session_id spid,OBJECT_NAME(resource_associated_entity_id) tableName from sys.dm_tran_locks where resource_typeOBJECTspid 锁表进程 tableName 被锁表名解锁&#x…

Centos 6.4下MySQL备份及还原详情介绍
我们前面文中中介绍了centos 6.4下MySQL的安装及配置,安装后为了保证数据的安全性所以我们同样也要学会备份及还原,备份及还原操作在我们的真实工作环境中是必不可少的,由于是对数据库数据备份,所以今天我们就随之介绍一下&#x…

iPhone 13 终于等到了!降价、新颜色、电池续航性能大提升
整理 | 禾木木、苏宓 出品 | AI科技大本营(ID:rgznai100) 它来了,真的来了! 不知有多少朋友守在今日凌晨观看一年一度的科技春晚——苹果发布会! 还是那个熟悉的样子,从加利福尼亚的沙漠中向我们走来&am…

“httpd未被被识别的服务”的解决办法
使用自动编译安装会出现这个问题,也就是输入 #service httpd restart 给出这样的提示;这时候要重启可以 #/usr/local/apache2/bin/apachectl start 如果你希望使用 #service httpd restart 那么需要按下面的做法 注意的是daemon /usr/local/apache…
安装sql 2005 闪退 连接到服务器失败。错误:0x80070424
可以尝试安装.net4.0 我是通过此办法解决。 本文转自 freeterman 51CTO博客,原文链接:http://blog.51cto.com/myunix/1751338,如需转载请自行联系原作者

简述DataInputStream和DataOuputStream
2019独角兽企业重金招聘Python工程师标准>>> Java开发中经常会用到IO流,那么就会碰到DataInputStream和DataOuputStream这两个包装类。下面就来简述一下这两种包装类的用法: 1.DataOutputStream:标准的数据输出流,将ja…

数字时代企业迎变局,如何让增长变简单?
随着企业数字化转型进入深水区,企业增长模式正迎来跨时代巨变:营销场景复杂且多变,用户触点丰富而分散, MarTech(营销技术)解决方案愈加碎片化,企业营销增长过程中各环节间的割裂,让…

Linux服务器网络开发模型
为什么Nginx的性能要比Apache高得多? 这主要是因为Nginx使用了最新的epoll(Linux 2.6内核)和kqueue(FreeBSD)网络I/O模型,而Apache则使用的是传统的select模型。曾在一篇博客上看到有这么个实例:假设你在大…

《从零开始学Swift》学习笔记(Day 47)——final关键字
在类的定义中使用final关键字声明类、属性、方法和下标。final声明的类不能被继承,final声明的属性、方法和下标不能被重写。 下面看一个示例: 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051final cl…

CentOS 5.5 编译安装apache+php+mysql,利用CMS快速建立论坛
这个是转来的,细节没有验证,请网友自己斟酌。。。。。。。。。。CentOS 5.5 编译安装apachephpmysql,利用CMS快速建立论坛1、安装Apache [rootbogon tmp]# wget http://labs.renren.com/apache-mirror/httpd/httpd-2.2.15.tar.bz2 [rootbogo…

SDT(software-defined Things)?软件定义的物件
物联网(IOT)的概念早在1999年就被宝洁公司的员工Kevin Ashton正式提出,可直到这最近几年才越来越火,无论国内外,但凡跟IOT 搭上点边的都能吸引众多的目光。2014年,投到智能硬件方向的风险资金就占到VC的一半…

赠书福利 | Tidio AI 趋势报告:约42%受访者能够接受机器人伴侣
编译 | 禾木木出品 | AI科技大本营(ID:rgznai100)文章内图源:Tidio近日,波士顿动力发布了一段机器人跳舞的视频,有些人不敢相信他们所看到的,它看起来更像是皮克斯动画而不是真实的镜头。有人说:…

Airlaunch 快捷设置代码分享
Airlaunch 快捷设置代码分享设置:prefs:rootSETTING蜂窝网络:prefs:rootMOBILE_DATA_SETTINGS_IDWIFI:prefs:rootWIFI定位服务:prefs:rootLOCATION_SERVICES蓝牙:prefs:rootBluetooth辅助功能:prefs:rootGe…

hdu3829(最大独立集)
传送门:Cat VS Dog 题意:动物园有N只猫,M只狗,P个小孩。每个小孩都有自己喜欢的动物和讨厌的动物,如果他喜欢狗,那么就讨厌猫, 如果他讨厌狗,那么他就喜欢猫。某个小孩能开心&#x…

数据科学家:那些年,我都学过哪些编程语言…
前言 我们对事物的看法各不相同,有时他人特别喜欢的语言可能会成为另一个人的的噩梦。而我个人的噩梦是用C语言进行日常的编程工作。 本文就介绍了作为一名数据科学家,我在职业生涯中所学过的语言,其中包括MATLAB、Weka、R、C 以及Python。 数…

short_open_tag 必须打开
在使用phpcms本地安装的过程中,到运行环境检测这一步,发现:short_open_tag 必须打开。 从网上搜索相关资料时,发现,将php.ini文件中的short_open_tag off 项,设置成on,重启服务器即可。 shor…

10.15 iptables filter表案例
2019独角兽企业重金招聘Python工程师标准>>> iptables常用知识回顾点 iptables -I/-A/-D 后紧跟 链 ,可以是INPUT,OUTPUT,FORWARDiptables -P 用来指定 链的默认策略 ——>最好不要直接操作,否则会造成远程的终端断…
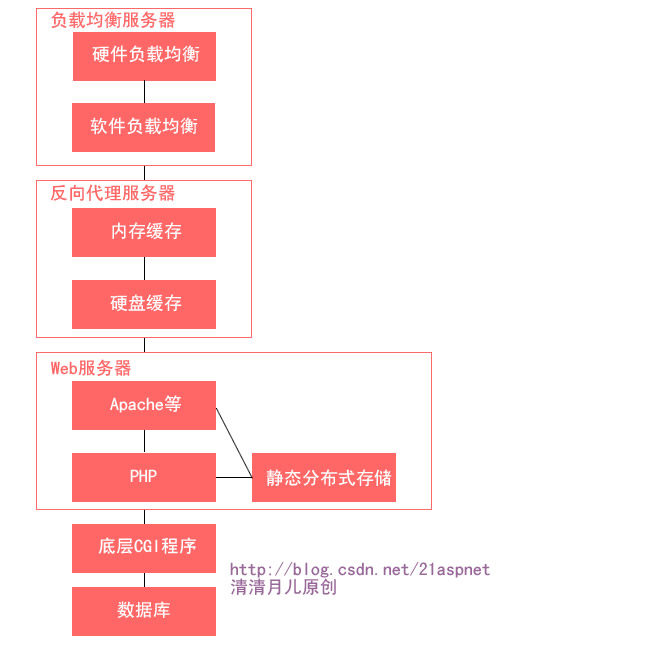
高并发大型网站架构设计
一个大型的网站网站应该由如下6个子系统组成 负载均衡系统 反向代理系统 Web服务器系统 分布式存储系统 底层服务系统 数据库集群系统 为什么要做高并发系统设计? 事实上,针对于任何单一的网络服务器程序,其可承受的同时连接数目是有理…

Tidio AI 趋势报告:约42%受访者能够接受机器人伴侣
编译 | 禾木木 出品 | AI科技大本营(ID:rgznai100) 文章内图源:Tidio 近日,波士顿动力发布了一段机器人跳舞的视频,有些人不敢相信他们所看到的,它看起来更像是皮克斯动画而不是真实的镜头。 有人说&#x…
微信公众平台对所有公众号开放自定义菜单
据统计,微信公众号已达1000多万了,但大多数没有微信认证,且没有开发能力,为此微信公众平台开放了自定义菜单功能给所有公众号,这是微信团队年前给广大自媒体送的大礼,期待微信越来越开放 公众帐号运营者点击…
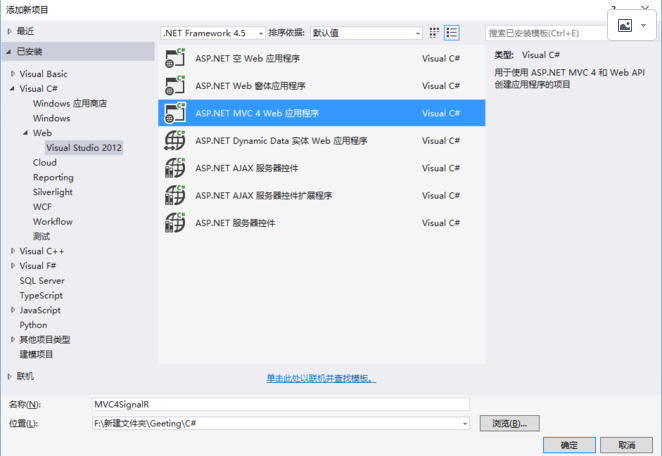
SignalR网页实时推送
1.新建项目,选择mvc4 Wed应用程序,选择Internet,视图引擎:Razor 2.在控制器中添加 并添加上视图 3.引用(install-package Microsoft.AspNet.SignalR) 4.添加Startup 项目名 5.新建Hubs文件夹,添…
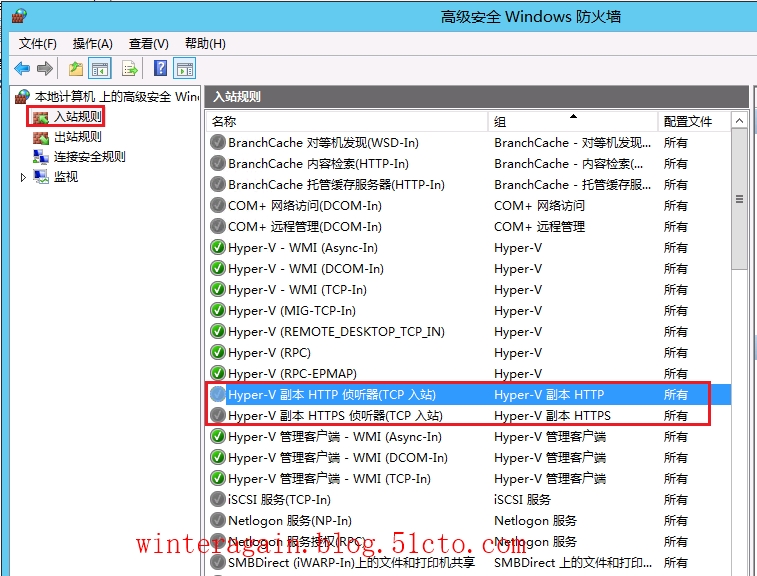
Hyper-V虚拟化测试05防火墙及证书配置
3.防火墙和证书3.1、防火墙配置打开Windows防火墙,并进入到高级配置入站规则,启用“Hyper-V副本HTTP侦听器(TCP入站)”和“Hyper-V副本HTTPS侦听器(TCP入站)”可以看到已经启用了如上两条规则允许入站流量3…

httpwatch的timechart 解析
从timeChart,我们可以一目了然的看到那些请求花费的时间较长,一般柱状的长短表示从请求到接受共花费的时间,我们重点需要优化那些柱状较长的部分,当然我们也可以点击time列,按请求时间排到序,直接找出请求时…

英特尔北京2022年冬奥会体验中心落成
2020年东京奥运会已圆满落幕,全社会进入到为北京2022年冬奥会紧锣密鼓筹备的倒计时模式。近日,“英特尔北京2022年冬奥会体验中心”在北京石景山区首钢园落成,并举办了媒体开放日活动。以体验中心为窗口,英特尔在近千平米的展厅中…

机器学习 LR getA()
机器学习 LR getA() 前面的几位回答都没有解决getA()是什么的问题,碰到同样的问题,解释如下:matrix.getA()Return self as an ndarray object.Equivalent to np.asarray(self).Parameters: None Returns: ret : ndarrayself as an ndarray 也…
memcache安装
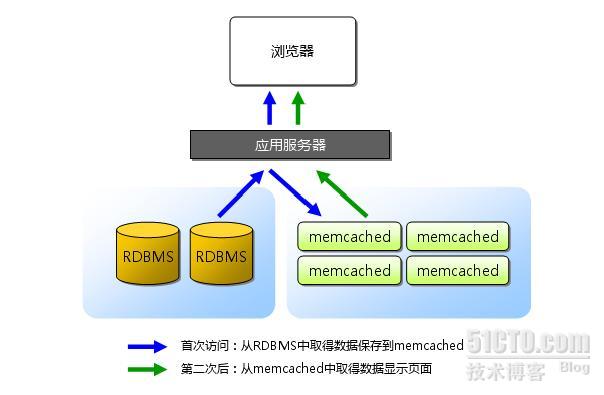
转载自 http://zhaochen.blog.51cto.com/2029597/390037 一,memcache简单介绍: memcached是高性能的分布式内存缓存服务器,为了提高性能,memcached中的数据都保存在内存中,重启memcached及重启操作系统都会导致缓存中的…

算法小论——第三章 又把新桃换旧符
2019独角兽企业重金招聘Python工程师标准>>> 笔记 这一章主要是渐进记号和高中数学的回忆。 几个标记: Θ -- 上界和下界,绑定值,相当于f(n) ∈ [c1 * g(n), c2 * g(n)]Ω -- 闭区间下界,最好运行时间,相当…

来体验一把职场人的真实训练,检验你的工程化交付能力!
长沙软件人才实训基地是由政府引导,长沙软件园(大型国企)、万兴科技(A股上市公司)和CSDN(中国开发者社区)三方参与,强强联手,倾力打造的人才培育平台,旨在通过…

从C#到Objective-C,循序渐进学习苹果开发(7)--使用FMDB对Sqlite数据库进行操作
本随笔系列主要介绍从一个Windows平台从事C#开发到Mac平台苹果开发的一系列感想和体验历程,本系列文章是在起步阶段逐步积累的,希望带给大家更好,更真实的转换历程体验。本篇主要开始介绍基于XCode进行IOS程序的开发,介绍使用FMDB…
