SIMD向量化运算
随着机器学习等人工智能技术的飞速发展,矩阵乘法的应用越来越多,intel芯片先后提供了不同系列的向量指令,包括mmx、sse、avx等,支持simd操作。后来为了更好地支持矩阵乘法,又增加了fma(Fused Multiply-Add)指令。fma指令需要三个向量参数va,vb,vcva,vb,vc,其效果等价于表达式(va∗vb)+vc(va∗vb)+vc,其中的乘法和加法都是面向向量中的元素的,也就是fma指令的结果是一个同样长度的向量。fma指令的出现为矩阵乘法提供了方便,但是其效果同样可以用avx指令系列中的乘法和加法的组合来实现,本文使用例子来分析不同向量指令在矩阵乘中的性能和精度。
例子主要计算了一个矩阵WW和向量xx的乘积,WW的列数等于xx的长度,结果仍然是一个向量,长度等于WW的行数。代码的实现如下。
#include <stdio.h>
#include <time.h>
#include <x86intrin.h>
int main() {
const int col = 1024, row = 64, num_trails = 1000000;
float w[row][col];
float x[col];
float y[row];
float scratchpad[8];
for (int i=0; i<row; i++) {
for (int j=0; j<col; j++) {
w[i][j]=(float)(rand()%1000)/800.0f;
}
}
for (int j=0; j<col; j++) {
x[j]=(float)(rand()%1000)/800.0f;
}
clock_t t1, t2;
// The original matrix multiplication version
t1 = clock();
for (int r = 0; r < num_trails; r++)
for(int j = 0; j < row; j++)
{
float sum = 0;
float *wj = w[j];
for(int i = 0; i < col; i++)
sum += wj[i] * x[i];
y[j] = sum;
}
t2 = clock();
float diff = ((float)t2 - (float)t1) / CLOCKS_PER_SEC;
printf("\nTime taken: %.2f second.\n", diff);
for (int i=0; i<row; i++) {
printf("%.4f, ", y[i]);
}
printf("\n");
// The avx matrix multiplication version.
const int col_reduced_8 = col - col % 8;
__m256 op0, op1, tgt, tmp_vec;
t1 = clock();
for (int r = 0; r < num_trails; r++)
for (int i=0; i<row; i++) {
float res = 0;
tgt = _mm256_setzero_ps();
for (int j = 0; j < col_reduced_8; j += 8) {
op0 = __builtin_ia32_loadups256(&x[j]);
op1 = __builtin_ia32_loadups256(&w[i][j]);
tmp_vec = __builtin_ia32_mulps256(op0, op1);
tgt = __builtin_ia32_addps256(tmp_vec, tgt);
}
__builtin_ia32_storeups256(scratchpad, tgt);
for (int k=0; k<8; k++)
res += scratchpad[k];
for (int l=col_reduced_8; l<col; l++) {
res += w[i][l] * x[l];
}
y[i] = res;
}
t2 = clock();
diff = ((float)t2 - (float)t1) / CLOCKS_PER_SEC;
printf("\nTime taken: %.2f second.\n", diff);
for (int i=0; i<row; i++) {
printf("%.4f, ", y[i]);
}
printf("\n");
// The fma matrix multiplication version.
t1 = clock();
for(int r = 0; r < num_trails; r++)
for(int i = 0; i < row; i++)
{
float rlt = 0;
tgt = _mm256_setzero_ps();
for(int j = 0; j < col_reduced_8; j += 8)
{
op0 = __builtin_ia32_loadups256(&x[j]);
op1 = __builtin_ia32_loadups256(&w[i][j]);
tgt = _mm256_fmadd_ps(op0, op1, tgt);
}
__builtin_ia32_storeups256(scratchpad, tgt);
for(int k = 0; k < 8; k++)
{
rlt += scratchpad[k];
}
for(int l = col_reduced_8; l < col; l++)
{
rlt += w[i][l] * x[l];
}
y[i] = rlt;
}
t2 = clock();
diff = ((float)t2 - (float)t1) / CLOCKS_PER_SEC ;
printf("\nTime taken: %.2f second.\n", diff);
for(int i=0; i<row; i++)
{
printf("%.4f, ", y[i]);
}
printf("\n");
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
在ubuntu系统中,程序的编译命令是:
gcc -O2 -mfma test.c -o test
需要注意的是,只有在支持fma的芯片结构下,程序才能够执行。可以通过命令:
cat /proc/cpuinfo | grep fma
来判断芯片是否支持fma。
其执行结果为:
Time taken: 93.56 second.
409.8341, 413.4546, 398.7332, 399.8303, 404.1195, 402.3861, 394.6979, 412.6429, 409.0014, 390.9019, 400.3911, 392.7900, 400.5019, 418.6781, 399.3336, 404.0719, 414.9839, 411.6887, 396.0086, 406.6972, 384.5781, 399.3724, 400.0473, 391.6383, 401.3511, 400.8543, 418.4066, 406.6425, 405.5102, 408.4534, 403.0285, 406.3510, 410.2005, 414.9617, 417.3602, 406.4511, 397.1705, 406.1265, 393.3314, 407.1777, 389.9053, 397.3145, 401.7866, 413.3134, 415.7482, 414.2341, 403.3439, 405.4922, 395.4076, 399.6389, 409.6675, 419.8184, 412.3336, 399.8252, 403.3434, 387.4861, 402.2747, 399.8241, 414.1568, 405.4861, 406.6151, 410.4040, 408.9755, 398.9610,
Time taken: 10.94 second.
409.8341, 413.4549, 398.7335, 399.8304, 404.1191, 402.3860, 394.6979, 412.6424, 409.0016, 390.9022, 400.3909, 392.7900, 400.5020, 418.6781, 399.3336, 404.0718, 414.9842, 411.6884, 396.0087, 406.6971, 384.5780, 399.3723, 400.0472, 391.6382, 401.3510, 400.8541, 418.4067, 406.6424, 405.5103, 408.4536, 403.0287, 406.3513, 410.2007, 414.9618, 417.3603, 406.4513, 397.1708, 406.1266, 393.3315, 407.1776, 389.9049, 397.3150, 401.7864, 413.3134, 415.7483, 414.2341, 403.3439, 405.4922, 395.4075, 399.6392, 409.6674, 419.8183, 412.3336, 399.8253, 403.3433, 387.4865, 402.2746, 399.8239, 414.1567, 405.4861, 406.6153, 410.4034, 408.9752, 398.9612,
Time taken: 12.08 second.
409.8341, 413.4549, 398.7335, 399.8304, 404.1191, 402.3860, 394.6979, 412.6424, 409.0016, 390.9022, 400.3909, 392.7900, 400.5021, 418.6781, 399.3336, 404.0718, 414.9842, 411.6884, 396.0087, 406.6971, 384.5780, 399.3722, 400.0472, 391.6382, 401.3510, 400.8541, 418.4067, 406.6424, 405.5102, 408.4536, 403.0287, 406.3513, 410.2007, 414.9618, 417.3603, 406.4513, 397.1708, 406.1266, 393.3315, 407.1776, 389.9050, 397.3150, 401.7864, 413.3134, 415.7483, 414.2341, 403.3439, 405.4922, 395.4075, 399.6392, 409.6674, 419.8183, 412.3336, 399.8253, 403.3433, 387.4865, 402.2746, 399.8239, 414.1568, 405.4861, 406.6153, 410.4034, 408.9752, 398.9612,
可见,avx对乘加的组合实现性能还略高于fma指令。而精度两者相似,略低于原始的运算。
---------------------
作者:softee
来源:CSDN
原文:https://blog.csdn.net/softee/article/details/55057476
版权声明:本文为博主原创文章,转载请附上博文链接!
相关文章:

【数据结构】二叉树及其相关操作
二叉树的定义 二叉树是一个由结点构成的有限集合,这个集合或者为空,或者由一个根节点及两棵互不相交的分别称作这个根节点的左子树和右子树的二叉树组成。 二叉树并非一般的树形结构的特殊形式,它们是两种不同的数据结构。 二叉树与一般树…

函数节流与函数防抖
什么是函数节流与函数防抖 举个栗子,我们知道目前的一种说法是当 1 秒内连续播放 24 张以上的图片时,在人眼的视觉中就会形成一个连贯的动画,所以在电影的播放(以前是,现在不知道)中基本是以每秒 24 张的速…

makefile 中 =, :=, ?=, +=的区别
在Makefile中我们经常看到 : ? 这几个赋值运算符,那么他们有什么区别呢?我们来做个简单的实验 新建一个Makefile,内容为: ifdef DEFINE_VRE VRE “Hello World!” else endif ifeq ($(OPT),define) VRE ? “Hello W…

ubuntu 编译源码包 dsc diff.gz orig.tar.gz
2019独角兽企业重金招聘Python工程师标准>>> 1) 在获取源码包之前,确保在软件源配置文件/etc/apt/sources.list中添加了deb-src项以tree实用程序(以树型结构获取目录树)为例,介绍Ubuntu中如何管理源码包&am…

【ACM】杭电OJ 2552
本来还查了atan 和 atan2 的用法,结果总是WA 看了解析之后才知道原来是要公式推导,最后得出所求的式子是一个等式,结果为1。 所以,以后出类似与数学公式的题,可能是要手算推到,在输出特定的结果。&#x…

蚂蚁金服天街:OceanBase 在大促 5 年来的技术演进
为了与金融从业者、科技从业者共同探讨金融 业务的深层次问题,蚂蚁金服联手 TGO 鲲鹏会,在 12 月 8 日举办了「走进蚂蚁金服:双十一背后的蚂蚁金服技术支持」活动。蚂蚁金服高级技术专家天街为大家分享了《蚂蚁双 11 大促 OceanBase 核心技术…

OTA升级flash分区
什么是在线OTA升级 - OTA是Over-the-Air的简写,空中下载技术的意思。 - OTA在线升级在日常消费电子产品中很常见,比如手机,机顶盒等,通过网络,下载升级数据包,更新操作系统等底层固件进行…

MD5与Base64的思考
MD5加密是对任意长的数据使用MD5哈稀算法散列为4个32位组,若格式化为ASCII字符则为16字符,若格式化16进制表示,则为32字符. (MD5的具体算法请参阅相关书籍和资料)MD5广泛用于数据校验和完整性检验.且不可逆.理论上为抗碰撞的在2004年8月17日,MD5遭遇重创,山东大学的王小云做了…
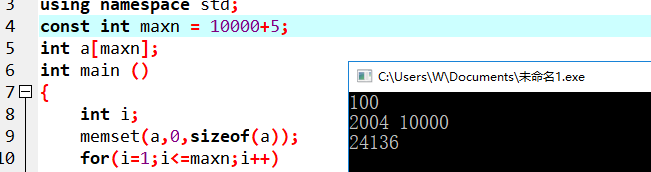
【ACM】杭电OJ 1076
数组要开的大一些,一开始数组只开到100005,就显示了错误的数据 AC代码: #include <iostream> #include <cstring> using namespace std; const int maxn 10000005; int a[maxn]; int main () {int i;memset(a,0,sizeof(a));fo…

IDEA ctrl+alt+L 格式化快捷键无效时解决
这几天发现自己Intellij IDEA ctrlaltL格式化代码无效 设置里面按照快捷键搜索 按了 ctrlaltL 也没反应 但是我设置的确实是默认的 ctrlaltL 最后终于找到了问题所在 原来是开网易云音乐的锅 网易云会有一个全局的快捷键ctrlaltL跟idea冲突 去网易云关了就好了 转载于:https:/…

gpio pin和pad的区别
PIN指芯片封装好后的管脚,即用户看到的管脚; PAD是硅片的管脚,是封装在芯片内部的,用户看不到。 PAD到PIN之间还有一段导线连接的。

【ACM】杭电OJ 1013
WA代码 输入很大的数的时候会输出“-1”,所以考虑用字符数组来储存输入的数据。 #include <iostream> #include <cstring> #include <cstdio> using namespace std; long long sum; long long fun (int n) {sum0;if(n<9) return n;while(n){s…

\\s+ split替换
出自: http://www.tuicool.com/articles/vy2ymm 详解 "\\s" 正则表达式中\s匹配任何空白字符,包括空格、制表符、换页符等等, 等价于[ \f\n\r\t\v] \f -> 匹配一个换页\n -> 匹配一个换行符\r -> 匹配一个回车符\t -> 匹配一个制表…
ubuntu18.04下双机驱动调试
环境搭建:https://blog.51cto.com/haidragon/2337256这里要先说下如果要下内核断点要先在编译前去掉写保护,但是下自己写的驱动可以不要。第二个最好编译完后压缩vm系统文件然后复制一份,这样就调试机与被调试机环境一模一样,同样…

如何独立开发一个网络请求框架
(原创出处为本博客:http://www.cnblogs.com/linguanh/) 目录: 前言 准备工作 开发模式 开发原则 线程 高并发 TCP/UDP 本类介绍 开发选择 功能列表 优点 拓展 完整代码 用法例子 前言: 已开源到GitHub,希望…

【ACM】杭电OJ 1284(待更)
#include<iostream> using namespace std; int main(){int n;while(cin>>n){int ans0; for(int i0;i<n/3;i){ //对3的个数进行枚举 int temp(n-3*i); //除了这i个3之外剩余的钱数 //temp/2,剩余部分换成2的总种类数,anstemp/21; //这…

c语言头文件中定义inline static相关函数的优劣
头文件中常见static inline函数,于是思考有可能遇到的问题,如头文件经常会被包含会不会产生很多副本?网上说法不一。于是自己验证。经过arm-none-eabi-gcc下测试后得出结论。 inline 关键字实际上仅是建议内联并不强制内联,gcc中O…

c语言inline详解
本文介绍了GCC和C99标准中inline使用上的不同之处。inline属性在使用的时候,要注意以下两点:inline关键字在GCC参考文档中仅有对其使用在函数定义(Definition)上的描述,而没有提到其是否能用于函数声明(Dec…

【ACM】杭电OJ 2090
题目中给出的四舍五入的条件可以忽略不计了,因为提交的程序没有考虑四舍五入,照样AC了 printf("%.1lf\n",sum); AC代码: 写的有点复杂了,其实不用定义结构体也可以。 #include<iostream> #include <cstdi…

属性配置文件详解(2)(十七)
过命令行设置属性值 相信使用过一段时间Spring Boot的用户,一定知道这条命令:java -jar xxx.jar --server.port8888,通过使用–server.port属性来设置xxx.jar应用的端口为8888。 在命令行运行时,连续的两个减号--就是对applicatio…

git track远程分支
在本地初始化仓库,提交代码时会出现,上游为空,当前分支为选择,等错误提示。其实就是本地仓库分支和远程仓库分支并未进行关联,即本地分支未追踪到远程分支。 1.本地和远程的状态 本地: 本地所有的文…

HTMLDOM中三种元素节点、属性节点、文本节点的测试案例
HTML dom中常用的三种节点分别是元素节点、属性节点、文本节点。 具体指的内容可参考下图: 以下为测试用例: <!DOCTYPE html> <html><head><title>元素节点、属性节点、文本节点的测试</title><meta name"Author" conte…

【ACM】DFS 全排列 回溯
深入体会一下DFS,回溯 在一些OJ上endl和“\n”还是有区别的!!! 题目链接:http://codevs.cn/problem/1294/ 方法一: #include <iostream> #include <cstdio> #include <cstring> usin…

(轉貼) 友達光電第五屆【A+種子暑期實習計畫】開始辦理報名 (News)
友達光電第五屆【A種子暑期實習計畫】開始辦理報名 友達光電以絕佳的團隊執行力,帶領台灣光電產業進入世界級的領域! 還在就學的你/妳,想成為世界級光電產業的A種子嗎? 把握最後的暑假加入友達的A種子實習團隊吧!! 【2008 A種子募集計畫】 實習期間&am…

binutils工具集用法
addr2line用于得到程序指令地址所对应的函数,以及函数所在的源文件名和行号。 在不少嵌入式开发环境中,编译器的名称往往不是gcc,而是想arm-rtems-gcc这样的,对于这种命名形式的编译器,读者通常可以找到arm-rtems-add…

【ACM】CODE[VS] 1215 (DFS)
题目描述 Description 在N*N的迷宫内,“#”为墙,“.”为路,“s”为起点,“e”为终点,一共4个方向可以走。从左上角((0,0)“s”)位置处走到右下角((n-1,n-1)“e”)位置处…

#大学#SQL基础学习笔记(02)
*数据分组select FAge,count(*) from TableName group by FAge (根据年龄进行分组)一般和聚合函数一起使用 *Having语句select FAge,count(*) from TableName group by FAge having count(*)>1 *聚合函数不能出现在where语句中 *having是对分组后的信息进行过滤,…

socket connect阻塞和非阻塞处理
建立socket后默认connect()函数为阻塞连接状态,在大多数实现中,connect的超时时间在75s至几分钟之间,想要缩短超时时间,可解决问题的两种方法:方法一、将socket句柄设置为非阻塞状态,方法二、采用信号处理函…

【ACM】CODE[VS] 2806(DFS)
感觉有点入了DFS的门槛,距离完全掌握还差得远呢 AC代码:运行时间为7ms #include <iostream> #include <cstdio> #include <cstring> using namespace std; const int maxn 26; int vis[maxn][maxn],col,line,flag,count; char map[…

scala学习手记34 - trait方法的延迟绑定
trait的方法的延迟绑定就是先混入的trait的方法会后调用。这一点从上一节的实例中也可以看出来。 下面再来看一个类似的例子: abstract class Writer {def write(message: String): String }trait UpperWriter extends Writer {abstract override def write(message…
