《Python数据分析与挖掘实战》一3.1 数据质量分析
本节书摘来自华章出版社《Python数据分析与挖掘实战》一书中的第3章,第3.1节,作者 张良均 王路 谭立云 苏剑林,更多章节内容可以访问云栖社区“华章计算机”公众号查看
3.1 数据质量分析
数据质量分析是数据挖掘中数据准备过程的重要一环,是数据预处理的前提,也是数据挖掘分析结论有效性和准确性的基础,没有可信的数据,数据挖掘构建的模型将是空中楼阁。
数据质量分析的主要任务是检查原始数据中是否存在脏数据,脏数据一般是指不符合要求,以及不能直接进行相应分析的数据。在常见的数据挖掘工作中,脏数据包括如下内容。
缺失值。
异常值。
不一致的值。
重复数据及含有特殊符号(如#、¥、*)的数据。
本小节将主要对数据中的缺失值、异常值和一致性进行分析。
3.1.1 缺失值分析
数据的缺失主要包括记录的缺失和记录中某个字段信息的缺失,两者都会造成分析结果的不准确,以下从缺失值产生的原因及影响等方面展开分析。
(1)缺失值产生的原因
1)有些信息暂时无法获取,或者获取信息的代价太大。
2)有些信息是被遗漏的。可能是因为输入时认为不重要、忘记填写或对数据理解错误等一些人为因素而遗漏,也可能是由于数据采集设备的故障、存储介质的故障、传输媒体的故障等非人为原因而丢失。
3)属性值不存在。在某些情况下,缺失值并不意味着数据有错误。对一些对象来说某些属性值是不存在的,如一个未婚者的配偶姓名、一个儿童的固定收入等。
(2)缺失值的影响
1)数据挖掘建模将丢失大量的有用信息。
2)数据挖掘模型所表现出的不确定性更加显著,模型中蕴涵的规律更难把握。
3)包含空值的数据会使建模过程陷入混乱,导致不可靠的输出。
(3)缺失值的分析
使用简单的统计分析,可以得到含有缺失值的属性的个数,以及每个属性的未缺失数、缺失数与缺失率等。
从总体上来说,缺失值的处理分为删除存在缺失值的记录、对可能值进行插补和不处理3种情况,将在4.1.1节详细介绍。
3.1.2 异常值分析
异常值分析是检验数据是否有录入错误以及含有不合常理的数据。忽视异常值的存在是十分危险的,不加剔除地把异常值包括进数据的计算分析过程中,对结果会产生不良影响;重视异常值的出现,分析其产生的原因,常常成为发现问题进而改进决策的契机。
异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称为离群点,异常值的分析也称为离群点分析。
(1)简单统计量分析
可以先对变量做一个描述性统计,进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出了合理的范围。如客户年龄的最大值为199岁,则该变量的取值存在异常。
(2)3原则
如果数据服从正态分布,在3原则下,异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。在正态分布的假设下,距离平均值3之外的值出现的概率为P(|x-|>3)≤0.003,属于极个别的小概率事件。
如果数据不服从正态分布,也可以用远离平均值的多少倍标准差来描述。
(3)箱型图分析
箱型图提供了识别异常值的一个标准:异常值通常被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;QU称为上四分位数,表示全部观察值中有四分之一的数据取值比它大;IQR称为四分位数间距,是上四分位数QU与下四分位数QL之差,其间包含了全部观察值的一半。
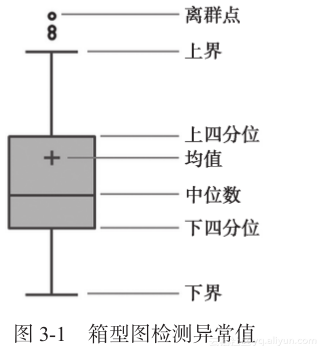
箱型图依据实际数据绘制,没有对数据作任何限制性要求(如服从某种特定的分布形式),它只是真实直观地表现数据分布的本来面貌;另一方面,箱型图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。由此可见,箱型图识别异常值的结果比较客观,在识别异常值方面有一定的优越性,如图3-1所示。
在餐饮系统中的销量额数据可能出现缺失值和异常值,如表3-1中数据所示。
分析餐饮系统日销量额数据可以发现,其中有部分数据
是缺失的,但是如果数据记录和属性较多,使用人工分辨的方法就不切合实际,所以这里需要编写程序来检测出含有缺失值的记录和属性以及缺失率个数和缺失率等。
在Python的Pandas库中,只需要读入数据,然后使用describe()函数就可以查看数据的基本情况。
import pandas as pd
catering_sale = '../data/catering_sale.xls' #餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期') #读取数据,指定“日期”列为索引列
data.describe()
运行结果如下。
销量
count 200.000000
mean 2755.214700
std 751.029772
min 22.000000
25% 2451.975000
50% 2655.850000
75% 3026.125000
max 9106.440000
其中count是非空值数,通过len(data)可以知道数据记录为201条,因此缺失值数为1。另外,提供的基本参数还有平均值(mean)、标准差(std)、最小值(min)、最大值(max)以及1/4、1/2、3/4分位数(25%、50%、75%)。更直观地展示这些数据,并且可以检测异常值的方法是使用箱线图。其Python检测代码如代码清单3-1所示。
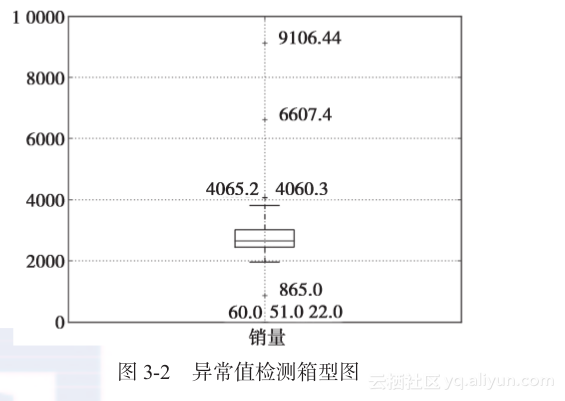
运行上面的程序,其结果为“缺失值个数为:1”,同时可以得到如图3-2所示的箱型图。
从图3-2中可以看出,箱型图中的超过上下界的7个销售额数据可能为异常值。结合具体业务可以把865、4060.3、4065.2归为正常值,将22、51、60、6607.4、9106.44归为异常值。最后确定过滤规则为:日销量在400以下5000以上则属于异常数据,编写过滤程序,进行后续处理。
3.1.3 一致性分析
数据不一致性是指数据的矛盾性、不相容性。直接对不一致的数据进行挖掘,可能会产生与实际相违背的挖掘结果。
在数据挖掘过程中,不一致数据的产生主要发生在数据集成的过程中,这可能是由于被挖掘数据是来自于从不同的数据源、对于重复存放的数据未能进行一致性更新造成的。例如,两张表中都存储了用户的电话号码,但在用户的电话号码发生改变时只更新了一张表中的数据,那么这两张表中就有了不一致的数据。
相关文章:
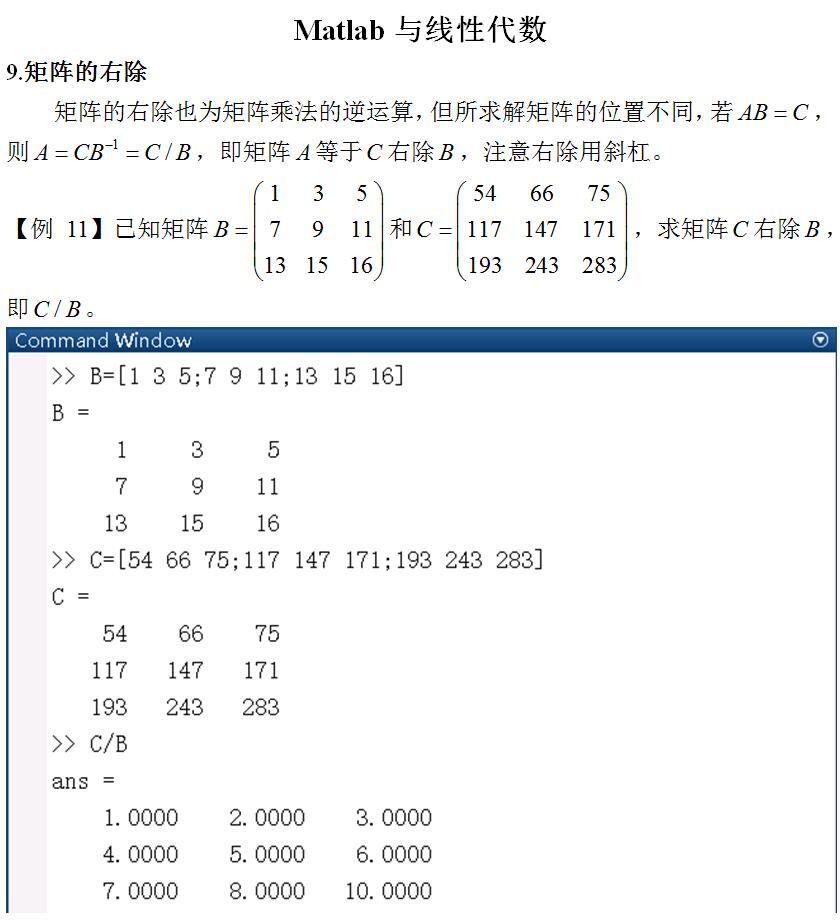
Matlab与线性代数 -- 矩阵的右除
打磨一项技能最需要的就是耐心,我们知道做一件事情不会一蹴而就,需要长时间的积累。关于Matlab的打磨会持续很长的时间,每天学习一个知识点,一年下来就不得了。要有耐心,要有耐心,跟着我们每天花5分钟的时间…

Java中的值传递和引用传递
当一个对象被当作参数传递到一个方法后,此方法可改变这个对象的属性,并可返回变化后的结果,那么这里到底是值传递还是引用传递? 答:是值传递。Java 编程语言只有值传递参数。当一个对象实例作为一个参数被传递到方法中时,参…

ASP.NET网站建设基本常用代码
1.为按钮添加确认对话框Button.Attributes.Add("onclick","return confirm(确认?)");Button.Attributes.Add("onclick","if(confirm(确定?)){return true;}else{return false;}") 2.表格超连接列传递参数<asp:HyperLinkColumn Ta…

C#语言与面向对象技术(6)
本图文主要掌握以下问题: 1.什么是“类型安全”问题? 2.为什么要引入泛型? 3.什么是泛型? 4.泛型是如何实现的? 5.类与类之间存在哪些关系,如何表示?

Xposed: 勾住(Hook) Android应用程序对象的方法,实现AOP
Xposed Xposed能够勾住(Hook) Android应用程序对象的方法,实现AOP,一个简单的例子: public class WebViewHook implements IXposedHookLoadPackage {// handleLoadPackage 会在android加载每一个apk后执行public void handleLoadPackage(Load…

Servlet防止页面被客户端缓存
服务器端的HttpServlet可通过设置特定HTTP响应头来禁止客户端缓存网页,以下示范代码中的response变量引用HttpServletResponse对象: response.addHeader("Pragma","no-cache"); response.setHeader("Cache-Control","…

二进制存储图片
二进制存储图片 如果我们要将一个图片文件二进制于数据库中,那么我们就必须将图片文件转化为二进制数据内容,再将二进制数据存储至数据库中,这是图片存储(或是其它文件数据库存储)的基本原则。 至于要从数据库中读取图…

《HTML5开发手册》——2.4 初学者“菜谱”:使用address元素提供通信信息
本节书摘来自异步社区《HTML5开发手册》一书中的第2章,第2.4节,作者: 【美】Chuck Hudson , 【英】Tom Leadbetter 更多章节内容可以访问云栖社区“异步社区”公众号查看。 2.4 初学者“菜谱”:使用address元素提供通信信息 规范中将address…

Matlab与线性代数 -- 矩阵的转置
打磨一项技能最需要的就是耐心,我们知道做一件事情不会一蹴而就,需要长时间的积累。关于Matlab的打磨会持续很长的时间,每天学习一个知识点,一年下来就不得了。要有耐心,要有耐心,跟着我们每天花5分钟的时间…

做为程序员对sql进行的性能优化
今天面试,我简历上写了熟悉sql的性能优化,但是今天面试,一时想不起别的,就仅仅说出了一条,在这里再总结一些,完善自己的知识点。 我经常用的数据库是oracle,所以我的sql优化是程序员针对于orac…

asp.NET自定义服务器控件内部细节系列教程四
如大家要转载,请保留本人的版权:/* *Description:asp.NET自定义服务器控件内部细节系列教程*Auther:崇崇-天真的好蓝 *MSN:chongchong2008msn.com *Dates:2007-05-20*Copyright:ChongChong2008 YiChang HuBei China */四 服务器控件相关元数据Attribute 1.设计期A…

《C++游戏编程入门(第4版)》——1.12 习题
本节书摘来自异步社区出版社《C游戏编程入门(第4版)》一书中的第1章,第1.1节,作者:【美】Michael Dawson(道森),更多章节内容可以访问云栖社区“异步社区”公众号查看。 1.12 习题 C…

Matlab与线性代数 -- 单位矩阵
打磨一项技能最需要的就是耐心,我们知道做一件事情不会一蹴而就,需要长时间的积累。关于Matlab的打磨会持续很长的时间,每天学习一个知识点,一年下来就不得了。要有耐心,要有耐心,跟着我们每天花5分钟的时间…
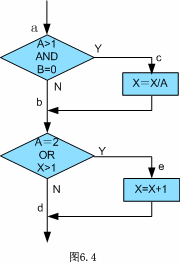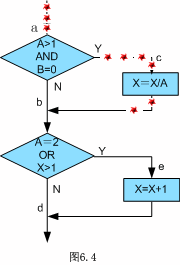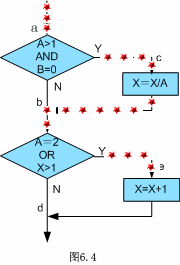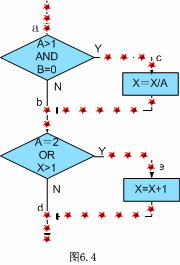
语句覆盖(Statement coverage)
一、语句覆盖(Statement coverage)“语句覆盖”是一个比较弱的测试标准,它的含义是:选择足够的测试用例,使得程序中每个语句至少都能被执行一次。 图6.4是一个被测试的程序,它的源程序…

RSS原理和实现
RSS是在互联网上被广泛采用的内容包装和投递协议。网络用户可以在客户端借助于支持RSS的新闻工具软件,在不打开网站内容页面的情况下,阅读支持RSS输出的网站内容。 1.RSS文件结构 示例: <?xml version"1.0" encoding"gb23…

consul安装配置使用
2019独角兽企业重金招聘Python工程师标准>>> 环境 centos:7.3 docker:1.12.6 kernel:3.10.0-514.6.1.el7.x86_64 consul:0.8.1 server1:10.1.13.221 server2:10.1.13.222 consul的功能 服务发现 健康检查 支持多数据中心 key/value存储 consul的使用场景 docker实例…

Matlab与线性代数 -- 全1矩阵
打磨一项技能最需要的就是耐心,我们知道做一件事情不会一蹴而就,需要长时间的积累。关于Matlab的打磨会持续很长的时间,每天学习一个知识点,一年下来就不得了。要有耐心,要有耐心,跟着我们每天花5分钟的时间…

java 冒泡排序和快速排序 实现
面试的时候经常会遇到面试官让你直接手写排序算法,下面是冒泡排序和快速排序的实现。冒泡排序基本流程就是,自下而上比较相邻的两个元素进行比较,让大的元素往下面沉,较小的往上冒。按照排序规则进行比较,如果是跟排序…

Matlab与线性代数 -- 零矩阵
打磨一项技能最需要的就是耐心,我们知道做一件事情不会一蹴而就,需要长时间的积累。关于Matlab的打磨会持续很长的时间,每天学习一个知识点,一年下来就不得了。要有耐心,要有耐心,跟着我们每天花5分钟的时间…

全球15个顶级技术类博客
1) 生活骇客(Lifehacker) http://www.lifehacker.com 生活骇客(Lifehacker)的座右铭表达了它的全部理念:“不要为技术而生活,要为生活而关注技术!”这个博客提供了有关于各方各面的“时间节省”…
[ExtJS5学习笔记]第五节 使用fontawesome给你的extjs5应用添加字体图标
本文地址:http://blog.csdn.net/sushengmiyan/article/details/38458411本文作者:sushengmiyan-------------------------------------------------资源链接--------------------------------------------------------FontAwesome glyph编码:…

正则式高人谈解答正则式的心得
条件1: 长度为14个字符 条件2: 其中任意9个位置为数字,并且数字只能是(0,1,3) 条件3: 其余的位置全部为"-"符号 ------------------------------------------ 求一个正则表达式 答案为:^(?!(.*?-){6,})(?…

数据结构与算法--线性表(顺序表)
本图文主要掌握以下问题: 1. 什么是线性表,线性表有哪些操作? 2. 如何利用顺序结构实现线性表?

Myeclipse在启动tomcat的时候的模式改变
在Myeclipse中, windows->preferences->Myeclipse->Servers->Tomcat 然后找到你的相应的Tomcat服务器的版本 当选择Debug mode的时候,当启动tomcat的时候,会进入debug视图 当选择Run mode的时候,启动tomcat的时候&a…

Request.ServerVariables参数集
Request.ServerVariables("Url") 返回服务器地址 Request.ServerVariables("Path_Info") 客户端提供的路径信息 Request.ServerVariables("Appl_Physical_Path") 与应用程序元数据库路径相应的物理路径 Request.ServerVariables("Path_T…

Linux (x86) Exploit 开发系列教程之十一 Off-By-One 漏洞(基于堆)
Off-By-One 漏洞(基于堆) 译者:飞龙 原文:Off-By-One Vulnerability (Heap Based) 预备条件: Off-By-One 漏洞(基于栈)理解 glibc mallocVM 配置:Fedora 20(x86ÿ…

利用链式存储结构实现线性表
本图文主要介绍了如何利用链式存储结构实现线性表。

自己用的快捷键
win7中 1. Ctrl Shift N —— 创建一个新的文件夹你需要在文件夹窗口中按 Ctrl Shift N 才行,在 Chrome 中是打开隐身窗口的快捷键。2.Win 上/下/左/右 —— 移动当前激活窗口其中,Win 左/右 为移动窗口到屏幕两边,占半屏,Wi…

3月到9月之9月到12月
看看自己这个博客,偶然发现上次的到现在又是半年过去了,这中间发生的太多,可能我天生不爱写东西,呵半年留一次脚印,真不知道我的博客对于博客园来讲算不算资源浪费!常看别人的,但自己没写过&…

