第七篇：数据预处理(四) - 数据归约(PCA/EFA为例)

前言

这部分也许是数据预处理最为关键的一个阶段。

如何对数据降维是一个很有挑战，很有深度的话题，很多理论书本均有详细深入的讲解分析。

本文仅介绍主成分分析法(PCA)和探索性因子分析法(EFA)，并给出具体的实现步骤。

主成分分析法 - PCA

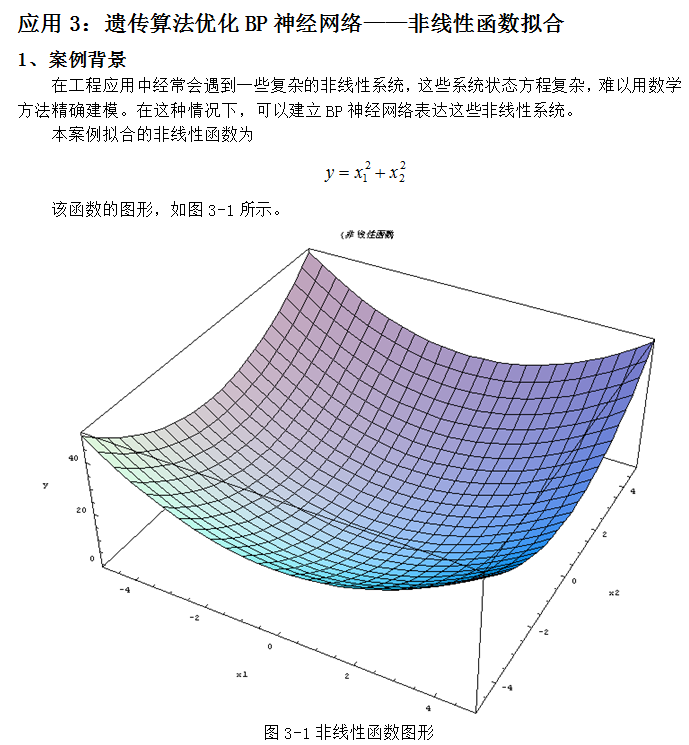
       主成分分析（principal components analysis， PCA）是一种分析、简化数据集的技术。

       它把原始数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标（第一主成分）上，第二大方差在第二个坐标（第二主成分）上，依次类推。主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分，忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是在处理观测数目小于变量数目时无法发挥作用，例如基因数据。

PCA基本步骤

       第一步：载入所需包和测试集数据：

       

       测试数据集内容大致如下：

       

       第二步：确定主成分的个数：

       

       在该函数中，fa是指定分析类型为主成分，n.iter是指平行分析中模拟测试的迭代次数为100次。结果如下：

       

       其中，蓝线为测试数据集中不同主成分对应的特征值折线图；红线为平行分析中模拟测试矩阵的不同主成分对应的特征值折线图。

       可采用以下几个思路来确定主成分的具体个数：

       1. 保留特征值大于1的主成分个数
       2. 根据图形弯曲的情况，选取图形变化最大处之上的特征值对应的主成分
       3. 特征值大于模拟矩阵的平均特征值的主成分保留

       根据这几个经验法则，可确定主成分的个数为1。

       当然，有一个更简单的确定方法 -- 在你调用fa.parallel函数之后，系统shell端会告诉你建议的主成分个数：

       

       第三步：提取主成分

       

       其中，nfactors是指定提取的主成分的个数。

       执行完毕后shell端打印如下信息：

       

       这些信息中，最重要的是载荷矩阵，也就是上方列为h2，u2的那个矩阵。

       我们只看PC1那一列(h2 u2先不去管它)，当然如果你指定的主成分个数是2，那么就会有PC2，以此类推。而行代表的则是每个特征。矩阵的值，也即载荷矩阵的值是数据集协方差矩阵对应的特征向量，也即这个主成分在该特征中所占的比重。如果你了解后面要讲的因子分析，那么也许会对这个表述产生疑惑 - 这不和因子一模一样吗？

       --- 答曰确实是的。主成分法本来就是选择因子的一种方法。事实上很多时候你也可以从载荷矩阵里观察得出主成分的现实意义。如果对主成分分析的结果不满意，可以尝试进行各种旋转以调整各个主成分所占的比重，具体请查阅principal函数的rotate参数。

       第四步：获取主成分得分

       

       得到结果如下：

       

       接下来就可以使用该主成分数据集了。

探索性因子分析法 - EFA

EFA的目标是通过发掘隐藏在数据下的一组较少的，更为基本的无法观测的变量，来解释一组可观测变量的相关性。这些虚拟的，无法观测的变量称作因子。(每个因子被认为可解释多个观测变量间共有的方差，也叫作公共因子)

模型的形式为：

Xi=a1F1+a2F2+……apFp+Ui

- Xi是第i个可观测变量（i=1,2,……k）；
       - Fj是公共因子（j=1,2,……p），并且p<k。

EFA基本步骤

第一步：载入所需包和测试集数据：

       第二步：确定因子个数

       

       这次分析的输入是数据集的相关矩阵(当然你也可以像PCA中讲的那样使用原始数据集)；n.obs是观测的样本数，这个参数只有在输入为协方差矩阵的时候需要；n.iter是指平行分析中模拟测试的迭代次数为100次，结果如下：

       

       该图的具体含义参考PCA部分讲解，根据同样方法选择因子个数为2。

       第三步：提取因子

       

       函数中，nfactors为因子个数；fm为提取因子的各种方法，有最大似然法(ml)，主轴迭代法(pa)，加权最小二乘法(wls)，广义加权最小二乘法(gls)和最小残差法(minres)等等，本文不细细分析此部分，请自行参阅相关文档。

       执行完毕后shell端打印如下信息：

       

       这些信息中，最重要的是载荷矩阵，也就是上方列有h2，u2等的那个矩阵。

       我们只看PA1和PA2这两列(h2 u2先不去管它)，当然如果你指定的因子个数是3，那么就会有PA3，以此类推。而行代表的则是每个特征。矩阵的值，也即载荷矩阵的值是这个因子在该特征中所占的比重。

       如果对因子分析的结果不满意，可以尝试进行各种旋转以调整各因子所占的比重，具体请查阅fa函数的rotate参数。

       第四步：分析特征间的潜在关系：

       

       该函数会图形化的显示载荷矩阵：

       

       图中的散点表示各个特征，而横纵轴则表示各个特征中的两个因子的占比重。

       还可以用下面这个函数，更为直观形象：

       

       结果显示如下：

       

       图中展示了各个因子在各个特征中的占比。此图可以很好地分析出因子的具体意义。

       第五步：提取各个样本的因子得分

       

       注意传递的数据必须是原数据集，如果传递进的是其协方差矩阵，那么这个得分值就没什么意义。

小结

       R语言的确方便的给出了很多算法的实现。然而，如果想要详细具体的知道如何调整参数，就必须要多去理解算法的思想，机制。

       这种能力是需要通过不断地学习算法，慢慢积累的。