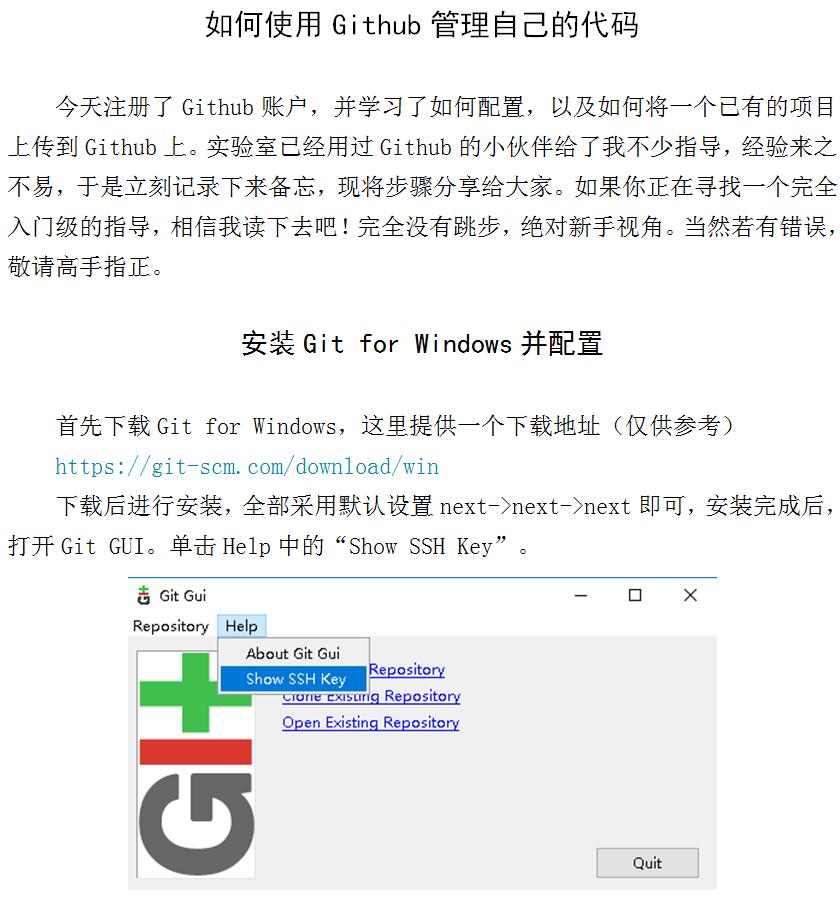
1、给定一个$n$个顶点$n$个边的图,边是$(i,a_{i})$,顶点编号$[0,n-1]$。增加一个顶点$n$,现在选出一个顶点集$M$,对于任意的在$M$中 的顶点$x$,去掉边$(x,a_{x})$,增加边$(x,n)$。最后使得顶点0和1相连。有多少种$M$?
思路:设从0开始可以遍历的顶点集合为$A$,从1可以遍历的顶点集合为$B$,$C=A\bigcap B$。令$A^{'}=A-C,B^{'}=B-C$。那么有下面的情况:
(1)在$C$中选择一些点(至少一个),从$A^{'},B^{'}$中任意选点;
(2)在$C$中不选择点,从$A^{'},B^{'}$中任意选点(不能为空);
(3)假设$C$不为空,那么可以不从$A^{'},B^{'},C$中选择。
对于不在$A^{'},B^{'},C$中的点都是随便选。
#include <stdio.h>
#include <string>
#include <stack>
#include <vector>
#include <string.h>
#include <algorithm>
#include <assert.h>
using namespace std;const int N=55;#define B(x) (1ll<<(x))class Sunnygraphs {
public:long long count(vector<int> a){int n=(int)a.size();vector<int> mask(n);for(int i=0;mask[i]<1;i=a[i]) mask[i]|=1;for(int i=1;mask[i]<2;i=a[i]) mask[i]|=2;int c[4]={0,0,0,0};for(int i=0;i<n;++i) ++c[mask[i]];long long ans=0;ans+=(B(c[3])-1)*B(c[1])*B(c[2]);ans+=(B(c[1])-1)*(B(c[2])-1);if(c[3]) ++ans;ans<<=c[0];return ans;}
};
2、给定$n$组数字$(a_{i},b_{i})$,$n$为偶数。现在重新排列这$n$组数字,得到新的$(A_{i},B_{i})$,使得下面的值最大:
$ans=\sum_{i=1}^{\frac{n}{2}}(B_{i}\sum_{j=1}^{i}A_{j})+\sum_{i=\frac{n}{2}+1}^{n}(B_{i}(X+\sum_{j=1}^{i}A_{j}))$
其中$2\leq n\leq 50,1\leq a_{i}\leq100000,1\leq b_{i}\leq10,0\leq X\leq 100000$
思路:现在考虑考虑最后分在前一半的两组$(A_{i},B_{i}),(A_{j},B_{j})$,若$i$在前优于$j$在前,那么$A_{i}B_{i}+(A_{i}+A_{j})B_{j}\geq A_{j}B_{j}+(A_{i}+A_{j})B_{i}$,即$A_{i}B_{j}\geq A_{j}B_{i}$。
由于$b_{i}$较小,现在枚举最后后一半的数字的所有的$A_{i}$之和$S$,那么现在对于一个数对,可以直接枚举它在前一半还是后一半(现在不管它在前一半还是后一半都可以直接计算对答案的贡献),这样可以进行动态规划。令$f[i][j][k]$表示现在已经考虑了$i$个数字,后一半数字的个数为$j$,后一半数字的$B$之和为$k$能得到的最大值,答案为$f[n][n/2][S]$。
#include <stdio.h>
#include <string>
#include <stack>
#include <vector>
#include <string.h>
#include <algorithm>
#include <assert.h>
using namespace std;int cmp(pair<int,int> a,pair<int,int> b)
{return a.first*b.second<b.first*a.second;
}int f[55][33][505];int A[55],B[55];void up(int &x,int y)
{if(x<y) x=y;
}int n;void DP(const int NextSumB,const int X)
{memset(f,-1,sizeof(f));f[0][0][0]=0;int pre=0;for(int i=1;i<=n;++i){pre+=B[i];for(int j=0;j<=n/2;++j) for(int k=0;k<=pre;++k){if(f[i-1][j][k]>=0){up(f[i][j][k],f[i-1][j][k]+A[i]*(pre-k)+A[i]*NextSumB);up(f[i][j+1][k+B[i]],f[i-1][j][k]+A[i]*B[i]+A[i]*k+X*B[i]);}}}
}class Moneymanager {public:int getbest(vector<int> a,vector <int> b,int X) {vector<pair<int,int> > p;n=(int)a.size();int sum=0;for(int i=0;i<n;++i) {p.push_back(make_pair(a[i],b[i]));sum+=b[i];}sort(p.begin(),p.end(),cmp);for(int i=1;i<=n;++i){A[i]=p[i-1].first;B[i]=p[i-1].second;}int ans=0;for(int i=0;i<=sum;++i){DP(i,X);ans=max(ans,f[n][n/2][i]);}return ans;}
};