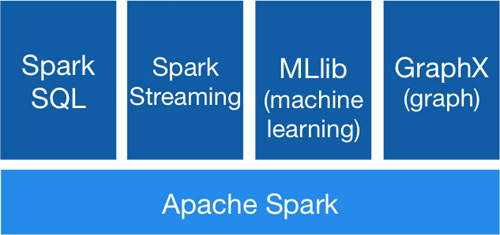
一、决策树简介
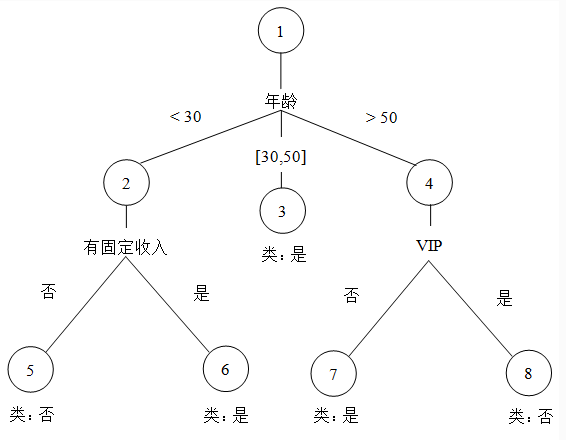
二、决策树的引导
 的取值为
的取值为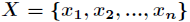 ,每一种取到的概率分别是
,每一种取到的概率分别是 ,那么
,那么 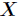 的熵定义为
的熵定义为 意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。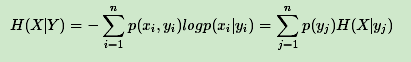
总结:在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略,以上 就是ID3算法的核心思想。
- 在给定的数据中,我们先选出信息增益最大的那个属性来作为根节点;
- 若样本都在同一类,则为叶子点;
- 将以作为节点的数据删除,再次寻找信息增益最大的那个属性进行分裂,不断递归;
- 递归结束标记为如下:
- 所有属性都用完,若所用属性都用完后还未分类完,则依照少数服从多数来看;
- 某一属性的分类结果都一致;
from math import log
import operator
dataSet = [[1,1,0,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],[0,0,1,'run'],[0,1,0,'fight'],[0,1,1,'run']] #需处理的数据
labels = ['weapon','bullet','blood'] #对应的标签
def calcShannonEnt(dataSet):numEntries = len(dataSet)lableCounts = {}for featVec in dataSet:currentLable = featVec[-1] #取数据中各元素的最后一项:类别if currentLable not in lableCounts.keys():lableCounts[currentLable] = 0lableCounts[currentLable] += 1 #给类别计数shannonEnt = 0for key in lableCounts:prob = float(lableCounts[key])/numEntriesshannonEnt -= prob * log(prob,2) #计算熵的值return shannonEnt #返回熵的值
def splitDataSet(dataSet,axis,value):retDataSet = [] #创建新列表retDataSet for featVec in dataSet:if featVec[axis] == value:reducedFeatVec = featVec[:axis]reducedFeatVec.extend(featVec[axis+1:])retDataSet.append(reducedFeatVec)return retDataSet
def chooseBestFeatureToSplit(dataSet):numFeatures = len(dataSet[0]) - 1 #减去最后一项(类别)baseEntropy = calcShannonEnt(dataSet)bestInfoGain = 0.0bestFeature = -1for i in range(numFeatures):featList = [example[i] for example in dataSet]uniqueVals = set(featList)newEntropy = 0.0for value in uniqueVals:subDataSet = splitDataSet(dataSet, i, value) #调用splitDataSet函数prob = len(subDataSet) / float(len(dataSet))newEntropy += prob * calcShannonEnt(subDataSet) #计算条件熵的值infoGain = baseEntropy -newEntropy #计算信息增益的值if infoGain > bestInfoGain:bestInfoGain = infoGainbestFeature = i #比较信息增益return bestFeature #返回信息增益最大的位置
'''因为我们递归构建决策树是根据属性的消耗进行计算的,所以可能会存在最后属性用完了,
但是分类还是没有算完,这时候就会采用多数表决的方式计算节点分类'''
def majorityCnt(classList):classCount = {}for vote in classList:if vote not in classCount.keys():classCount[vote] = 0classCount[vote] += 1return max(classCount) #返回多数表决后的结果
def createTree(dataSet, labels):classList = [example[-1] for example in dataSet]if classList.count(classList[0]) ==len(classList):return classList[0] #所有类别都相同则停止划分,直接返回该类别if len(dataSet[0]) == 1: #所有特征已经用完return majorityCnt(classList) #返回多数表决后的结果bestFeat = chooseBestFeatureToSplit(dataSet) #调用chooseBestFeatureToSplit函数bestFeatLabel = labels[bestFeat]myTree = {bestFeatLabel:{}}del(labels[bestFeat]) #删除信息增益最大的位置对应的标签featValues = [example[bestFeat] for example in dataSet]uniqueVals = set(featValues)for value in uniqueVals:subLabels = labels[:] #为了不改变原始列表的内容复制了一下myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)return myTree
myTree = createTree(dataSet,labels)
print myTree
{'weapon': {0: {'blood': {0: 'fight', 1: 'run'}}, 1: 'fight'}}
七、ID3算法的缺点
- ID3算法往往偏向于选择取值较多的属性,而在很多情况下取值较多的属性并不总是最重要的属性;
- ID3算法不能处理具有连续值的属性,也不能处理具有缺失数据的属性;
- ID3算法虽然理论清晰,但计算比较复杂,在学习和训练数据集的过程中机器内存占用率比较大,耗费资源;
- 在建造决策树时,每个结点仅含一个属性,是一种单变元的算法,致使生成的决策树结点之间的相关性不够强,虽然在一棵树上连在一起,但联系还是松散的;