如何使用netwokx进行复杂网络的中心性分析?
如何使用netwokx进行复杂网络的中心性分析?
这是本学期在大数据哲学与社会科学实验室做的第七次分享了。
第一次分享的是:
- 如何利用“wordcloud+jieba”制作中文词云?
第二次分享的是:
- 如何爬取知乎中问题的回答以及评论的数据?
第三次分享的是:
- 如何利用百度AI平台或snownlp做中文文本的情感分析?
第四次分享的是:
- 如何利用情感词典做中文文本的情感分析?
第五次分享的是:
- 如何利用pyecharts绘制酷炫的桑基图?
- 如何在Jupyter Lab中显示pyecharts的图形?
第六次分享的是:
- 如何利用pyecharts绘制炫酷的关系网络图?
本次分享的是“如何使用netwokx进行复杂网络的中心性分析?”
1. networkx概述
networkx是用python语言编写的软件包,便于用户对复杂网络进行创建、操作和学习。
利用networkx可以以标准化和非标准化的数据格式存储网络、生成多种随机网络和经典网络、分析网络结构、建立网络模型、设计新的网络算法、进行网络绘制等。
使用pip安装当前版本的networkx:
pip install networkx
升级到最新版本,使用–upgrade标签:
pip install --upgrde networkx
查看本地networkx是否成功安装,可在命令提示符中输入:
pip show networkx
如果出现以下内容,则安装成功。
Name: networkx
Version: 2.5.1
Summary: Python package for creating and manipulating graphs and networks
Home-page: http://networkx.github.io/
Author: Aric Hagberg
Author-email: hagberg@lanl.gov
License: UNKNOWN
Location: c:\programdata\anaconda3\lib\site-packages
Requires: decorator
Required-by: scikit-image
Github地址:
https://github.com/networkx/networkx
官方学习文档:
https://networkx.github.io/documentation/latest/_downloads/networkx_reference.pdf
2. 基本理论
网络由节点(node)和连接它们的边(edge)构成。
例如,微信好友的关系是相互的,如果我是你的好友,你也是我的好友。这样的网络称为无向网络(undirected graph/network)。但超链接并非如此,如果我的网站可以链接到维基百科,并不表示维基百科会链接到我的网站。这样的网络称为有向网络(directed graph/network)。
在图论和网络分析中,中心性(Centrality)是判断网络中节点重要性/影响力的指标。在社会网络分析中,一项基本的任务就是鉴定一群人中哪些人比其他人更有影响力,从而帮助我们理解他们在网络中扮演的角色。
那么,什么样的节点是重要的呢?
对节点重要性的解释有很多,不同的解释下判定中心性的指标也有所不同。
通常在中心性的分析角度上有两种出发点:中心度和中心势。
中心度:表示一个节点在网络中处于核心地位的程度;中心势:表示整个图的紧密程度。换句话说,度表示单个节点的性质,而势表示整个图的性质。
2.1 点度中心性(degree centrality)
在无向网络中,我们可以用一个节点的度数(相当于你的微信好友数)来衡量中心性。在微博中,刘德华的粉丝数9千多万,他的点度中心性就很高。
这一指标背后的假设是:重要的节点就是拥有许多连接的节点。你的社会关系越多,你的影响力就越强。
import networkx as nx
import matplotlib.pyplot as pltG = nx.Graph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
G.add_edges_from([('A', 'B'), ('A', 'C'), ('A', 'D'),('B', 'C'), ('B', 'D'), ('C', 'D'),('D', 'E'), ('D', 'F'), ('D', 'G'),('E', 'F'), ('E', 'G'), ('F', 'G')])pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True)
plt.show()

在上面的蝴蝶结网络中,节点DDD的连接数是6,和网络中的所有人都建立了直接联系,其它节点的连接数都是3,因此节点DDD的点度中心性最高。整个网络一共有7个节点,意味着每个人最多可以有6个社会关系。因此,节点DDD的点度中心性是6/6=1,其它节点的点度中心性是3/6=0.5。
dc(v)=degree(v)n−1dc(v)=\frac{degree(v)}{n-1} dc(v)=n−1degree(v)
2.2 中介中心性(betweenness centrality)
网络中两个非相邻成员之间的相互作用依赖于其它成员,特别是两成员之间路径上的那些成员。他们对两个非相邻成员之间的相互作用具有控制和制约作用。Freeman (1979)认为中间成员对路径两端的成员具有“更大的人际关系影响”。因此,中介中心性的思想是:如果一个成员位于其它成员的多条最短路径上,那么该成员就是核心成员,就具有较大的中介中心性。
计算网络中任意两个节点的所有最短路径,如果这些最短路径中很多条都经过了某个节点,那么就认为这个节点的中介中心性高,这个指标考察的是节点对于其它节点信息传播的控制能力。换句话说,就是这个节点相当于一个闸,和它相连的节点想要得到其它节点都得经过它。
G = nx.Graph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
G.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'C'),('B', 'D'), ('D', 'E'), ('E', 'F'),('E', 'G'), ('F', 'G')])pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True)
plt.show()
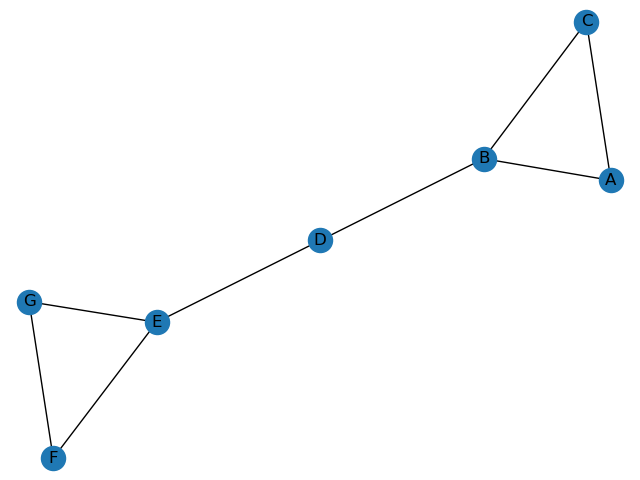
假设我们要计算节点DDD的中介中心性。
首先,我们计算节点DDD之外,所有节点对之间的最短路径有多少条,这里是15条(在6个节点中选择两个节点即节点对的个数)。
然后,我们再看所有这些最短路径中有多少条经过节点DDD,例如节点AAA要想找到节点EEE,必须经过节点DDD。经过节点DDD的最短路径有9条。
最后,我们用经过节点DDD的最短路径除以所有节点对的最短路径总数,这个比率就是节点DDD的中介中心性。节点DDD的中介中心性是9/15=0.6。
bs(v)=∑s≠t≠v∈Vdst(v)dstbs(v)=\sum_{s\neq t\neq v\in V}\frac{d_{st}(v)}{d_{st}} bs(v)=s=t=v∈V∑dstdst(v)
- dstdstdst表示sss到ttt的最短路径条数。
- dst(v)dst(v)dst(v)表示从sss到t的最短路径中经过节点vvv的条数。
Maksim Tsvetovat&Alexander Kouznetsov在《社会网络分析》一书中有两个例子:
- 鲍勃徘徊在两个女人之间,他贪恋爱丽丝的美丽和谈吐,亦无法舍弃卡若琳娜的乐天和无忧无虑。但他必须小心谨慎,生怕自己在其中任何一个人面前露馅,这样的关系充满了压力和焦虑。
- 银行家以5%的利率接受A公司的存款,以7%的利率贷款给B公司,这样的关系给银行家带来了巨大的利益。它的前提是,市场中的A公司和B公司不能直接接触,或至少无法轻易地找到对方。
鲍勃和银行家的故事尽管截然不同,但他们都处于一种被称为被禁止的三元组(forbidden triad)的关系中,需要确保三元组的末端不能直接联系。没有联系就像网络中出现了一个洞,因此也被称为结构洞。
2.3 接近中心性(closeness centrality)
点度中心性仅仅利用了网络的局部特征,即节点的连接数有多少,但一个人连接数多,并不代表他/她处于网络的核心位置。接近中心性和中介中心性一样,都利用了整个网络的特征,即一个节点在整个结构中所处的位置。如果节点到图中其它节点的最短距离都很小,那么它的接近中心性就很高。相比中介中心性,接近中心性更接近几何上的中心位置。

接近中心性反应某一节点与其它节点之间的接近程度。
假设我们要计算节点DDD的接近中心性,首先我们计算从节点DDD到所有其它节点的最短距离。从图中可以判断,节点DDD到所有其它节点的距离均为1,距离之和为6。因此,节点DDD的接近中心性为(7-1)/6=1。分子为网络中节点总数减去1。也就是说,如果一个人可以直接跟网络中所有其他人联系,那么他/她的接近中心性就是1。对于其它节点,如节点AAA的接近中心性为(7-1)/9=0.667。
接近中心性高的节点一般扮演的是八婆的角色(gossiper)。他们不一定是名人,但是乐于在不同的人群之间传递消息。
cc(v)=\frac{n-1}{\sum_{v\neq u}{d_{vu}}}
2.4 特征向量中心性(eigenvector centrality)
特征向量中心性的基本思想是,一个节点的中心性是相邻节点中心性的函数。也就是说,与你连接的人越重要,你也就越重要。
特征向量中心性和点度中心性不同,一个点度中心性高,即拥有很多连接的节点,特征向量中心性不一定高,因为所有的连接者有可能特征向量中心性很低。同理,特征向量中心性高并不意味着它的点度中心性高,它拥有很少但很重要的连接者也可以拥有高特征向量中心性。
考虑下面的图,以及相应的5×55\times 55×5的邻接矩阵(Adjacency Matrix),AAA。
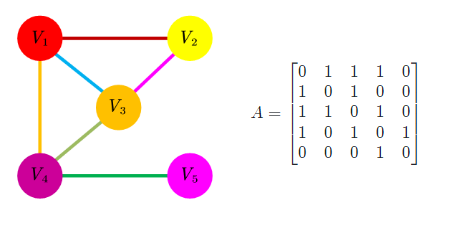
邻接矩阵的含义是,如果两个节点没有直接连接,记为0,否则记为1。
现在考虑xxx,一个5×15\times 15×1的向量,向量的值对应图中的每个点。在这种情况下,我们计算的是每个点的点度中心性(degree centrality),即以点的连接数来衡量中心性的高低。
矩阵AAA乘以这个向量的结果是一个5×15\times 15×1的向量:
Ax=[0111010100110101010100010][32331]=[86873]Ax= \begin{bmatrix} 0&1&1&1&0\\ 1&0&1&0&0\\ 1&1&0&1&0\\ 1&0&1&0&1\\ 0&0&0&1&0\\ \end{bmatrix}\begin{bmatrix} 3\\ 2\\ 3\\ 3\\ 1\\ \end{bmatrix}=\begin{bmatrix} 8\\ 6\\ 8\\ 7\\ 3\\ \end{bmatrix} Ax=⎣⎢⎢⎢⎢⎡0111010100110101010100010⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡32331⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡86873⎦⎥⎥⎥⎥⎤
结果向量的第一个元素是用矩阵AAA的第一行去“获取”每一个与第一个点有连接的点的值(连接数,点度中心性),也就是第2个、第3个和第4个点的值,然后将它们加起来。
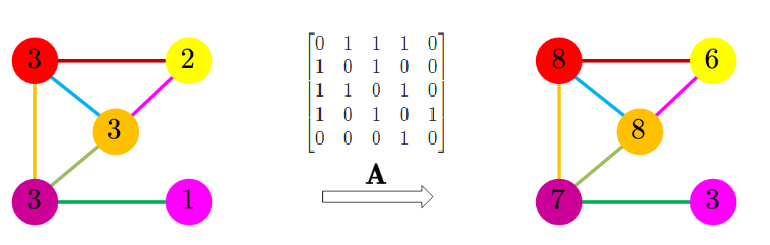
我们继续用矩阵AAA乘以结果向量。如何理解呢?实际上,我们允许这一中心性数值再次沿着图的边界“扩散”。我们会观察到两个方向上的扩散(点既给予也收获相邻节点)。我们猜测,这一过程最后会达到一个平衡,特定点收获的数量会和它给予相邻节点的数量取得平衡。既然我们仅仅是累加,数值会越来越大,但我们最终会到达一个点,各个节点在整体中的比例会保持稳定。
我们认为,图中的点存在一个数值集合,对于它,用矩阵AAA去乘不会改变向量各个数值的相对大小。也就是说,它的数值会变大,但乘以的是同一个因子。用数学符号表示就是:
x(t+1)=cAx(t)x(t+1)=cAx(t) x(t+1)=cAx(t)
Ax=λxAx=\lambda x Ax=λx
满足这一属性的向量就是矩阵AAA的特征向量。特征向量的元素就是图中每个点的特征向量中心性。
3. 克拉克哈特风筝社交网络分析
绘制克拉克哈特风筝社交网络
import networkx as nx
import matplotlib.pyplot as pltG = nx.krackhardt_kite_graph()
pos = nx.spring_layout(G)nx.draw(G, pos, with_labels=True)
plt.show()
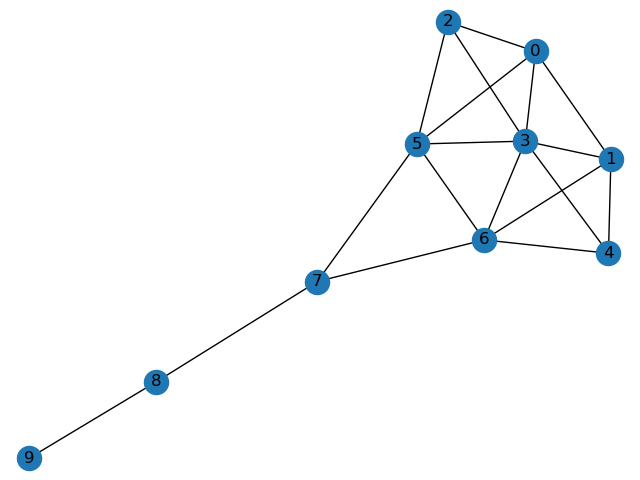
显示图的基本信息
print(nx.nodes(G))
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]print(nx.number_of_nodes(G)) # 10
print(nx.edges(G))
# [(0, 1), (0, 2), (0, 3), (0, 5), (1, 3), (1, 4),
# (1, 6), (2, 3), (2, 5), (3, 4), (3, 5), (3, 6),
# (4, 6), (5, 6), (5, 7), (6, 7), (7, 8), (8, 9)]print(nx.number_of_edges(G)) # 18
print(nx.adjacency_matrix(G))
# (0, 1) 1
# (0, 2) 1
# (0, 3) 1
# (0, 5) 1
# (1, 0) 1
# (1, 3) 1
# (1, 4) 1
# (1, 6) 1
# (2, 0) 1
# (2, 3) 1
# (2, 5) 1
# (3, 0) 1
# (3, 1) 1
# (3, 2) 1
# (3, 4) 1
# (3, 5) 1
# (3, 6) 1
# (4, 1) 1
# (4, 3) 1
# (4, 6) 1
# (5, 0) 1
# (5, 2) 1
# (5, 3) 1
# (5, 6) 1
# (5, 7) 1
# (6, 1) 1
# (6, 3) 1
# (6, 4) 1
# (6, 5) 1
# (6, 7) 1
# (7, 5) 1
# (7, 6) 1
# (7, 8) 1
# (8, 7) 1
# (8, 9) 1
# (9, 8) 1A = nx.to_numpy_matrix(G)
print(A)
# [[0. 1. 1. 1. 0. 1. 0. 0. 0. 0.]
# [1. 0. 0. 1. 1. 0. 1. 0. 0. 0.]
# [1. 0. 0. 1. 0. 1. 0. 0. 0. 0.]
# [1. 1. 1. 0. 1. 1. 1. 0. 0. 0.]
# [0. 1. 0. 1. 0. 0. 1. 0. 0. 0.]
# [1. 0. 1. 1. 0. 0. 1. 1. 0. 0.]
# [0. 1. 0. 1. 1. 1. 0. 1. 0. 0.]
# [0. 0. 0. 0. 0. 1. 1. 0. 1. 0.]
# [0. 0. 0. 0. 0. 0. 0. 1. 0. 1.]
# [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]]dic = dict((x, list(nx.neighbors(G, x))) for x in nx.nodes(G))
print(dic)
# {0: [1, 2, 3, 5], 1: [0, 3, 4, 6], 2: [0, 3, 5],
# 3: [0, 1, 2, 4, 5, 6], 4: [1, 3, 6], 5: [0, 2, 3, 6, 7],
# 6: [1, 3, 4, 5, 7], 7: [5, 6, 8], 8: [7, 9], 9: [8]}
中心性分析
deg_cen = nx.degree_centrality(G)
print(deg_cen)
# {0: 0.4444444444444444, 1: 0.4444444444444444, 2: 0.3333333333333333,
# 3: 0.6666666666666666, 4: 0.3333333333333333, 5: 0.5555555555555556,
# 6: 0.5555555555555556, 7: 0.3333333333333333, 8: 0.2222222222222222,
# 9: 0.1111111111111111}bet_cen = nx.betweenness_centrality(G)
print(bet_cen) #
# {0: 0.023148148148148143, 1: 0.023148148148148143, 2: 0.0,
# 3: 0.10185185185185183, # 4: 0.0, 5: 0.23148148148148148, 6: 0.23148148148148148,
# 7: 0.38888888888888884, 8: 0.2222222222222222, 9: 0.0}clo_cen = nx.closeness_centrality(G)
print(clo_cen)
# {0: 0.5294117647058824, 1: 0.5294117647058824, 2: 0.5,
# 3: 0.6, 4: 0.5, 5: 0.6428571428571429, 6: 0.6428571428571429,
# 7: 0.6, 8: 0.42857142857142855, 9: 0.3103448275862069}eig_cen = nx.eigenvector_centrality(G)
print(eig_cen)
# {0: 0.35220898139203594, 1: 0.35220898139203594, 2: 0.2858347353163241,
# 3: 0.4810204881221006, 4: 0.2858347353163241, 5: 0.3976910106255469,
# 6: 0.3976910106255469, 7: 0.19586185175360382, 8: 0.04807477501420294,
# 9: 0.011164058575824238}
4. 总结
- 点度中心性:一个人的社会关系越多,他/她就越重要。
- 中介中心性:如果一个成员处于其他成员的多条最短路径上,那么该成员就是核心成员。
- 接近中心性:一个人跟所有其他成员的距离越近,他/她就越重要。
- 特征向量中心性:与你连接的人社会关系越多,你就越重要。
参考文献:
- https://blog.csdn.net/yyl424525/article/details/103108506
- https://blog.csdn.net/ztf312/article/details/107711916
- https://blog.csdn.net/teacherfbj/article/details/106165429
相关文章:

Redis 笔记系列(十一)——Redis的发布和订阅机制
2019独角兽企业重金招聘Python工程师标准>>> 本文说的redis功能没啥大用处,大家知道有这回事情就好,我一笔带过。 Redis的发布订阅 这是什么 进程间的一种消息通信模式:发送者(pub)发送消息,订阅者(sub)接收消息。 例如…

界面交互推荐-25个闪亮创意的404错误页面设计-你从中发现了什么
404错误页面是站长和用户都很不愿见到的页面,因为那意味着该网站不能访问。但404错误是没人能避免,如服务器出现问题,站内需要调整,收到攻击等,我们访问网站的时候,一旦遇到404提示,我们那时的感觉是相当差…

参加完Python培训可以做什么
大家都知道Python在互联网行业是很吃香的,但是参加完Python培训之后,很多人都不知道该从哪个职业方向做起,下面小编就为大家详细的介绍一下参加完Python培训可以做什么? 参加完Python培训可以做什么?目前来看,Python发展得还是不…

my domain
www.yyhcy.co.cc hcy.sourceforge.net转载于:https://www.cnblogs.com/nbalive2001/archive/2012/10/25/2738086.html
【青少年编程】【Scratch】04 事件模块
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 微信后台回复“资料下载”可获取以往学习的材料(视频、代码、文档&…

1.随机函数,计算机运行的基石
待地铁的时间-在区间(a,b)上均匀分布的随机函数 rnd(1)是产生一个p (0 rnd(1) x (b-a) a 增量 基数 // 进行一系列的重复独立试验,每个试验的结果只有二个, 一个结果出现的概率总是p,另一个结果总是q, 称为贝努利试验 至一个结果出现所进行…

java培训班如何选择
想要进军互联网行业,大多数人的选择都是java技术,java技术在互联网行业是非常稳定的,那么学习java技术的话,java培训班如何选择呢?来看看下面的详细介绍。 java培训班如何选择?主要参考以下几点: 第一,选…

谢文睿:西瓜书 + 南瓜书 吃瓜系列 4. 二分类线性判别分析
Datawhale南瓜书是经典机器学习教材《机器学习》(西瓜书)的公式推导解析指南,旨在让在学习西瓜书的过程中,再也没有难推的公式,学好机器学习。 以往内容: 西瓜书公式推导讲解来了!0. 导学1. 一…

二叉排序树的相关操作
#include <IOSTREAM.H> #include <STDLIB.H> //二叉树的生成和释放 typedef struct Node {int data;struct Node * pParent;struct Node * pLeftChild;struct Node * pRightChild; }Node;Node * Create_BTree(int *array,Node* pParentNULL)//二叉排序树的创建,按照…

IDEA的常用操作(快捷键)
Alt回车 导入包,自动修正 CtrlN 查找类 CtrlShiftN 查找文件 CtrlAltL 格式化代码 CtrlAltO 优化导入的类和包 AltInsert 生成代码(如get,set方法,构造函数等) CtrlE或者AltShiftC 最近更改的代码 CtrlR 替换文本 CtrlF 查找文本 CtrlShiftSpace 自动补全代码 Ctrl空格 代码提示…

UI设计培训分享:ui的字体怎么正确设置?
UI设计工作中,UI字体设计是非常重要且频繁使用的一个工作内容之一,对于字体的设计也是非常需要进行注意的,本期小编为大家介绍的UI设计培训内容就是关于ui的字体怎么正确设置?来看看下面详细介绍。 UI设计培训分享:ui的字体怎么正…

【译文转帖】用C#写COM组件 Building COM Objects in C#
说明: 我是一个C#程序员,但是有一次一个需求只能用C/C去写,恰好需要读取的数据存放在DB(SQL CE v3)里面,而我又不会C/C(关键是用OleDB访问DB,这个实在是繁琐),所以催生了用C#写一个COM组件,用C/C去调用的想法.可谓,很傻很天真.但是也是一种思路,如果MS提供C API的话,问题就简单…

apache 开启 gzip 压缩服务
2019独角兽企业重金招聘Python工程师标准>>> 1、打开 apache 的 "httpd.conf" 文件,找到以下这一行,将它前面的注释(#)去掉: LoadModule deflate_module modules/mod_deflate.so 2、在 httpd.con…

Scratch等级考试(二级)模拟题
青少年编程竞赛交流群已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 微信后台回复“资料下载”可获取以往学习的材料(视频、代码、文档&…

找Java培训机构有哪些评判标准
想要学习java技术,找java培训机构是大多数人的选择,目前市面上的java培训机构有很多,用什么评判标准来找到时候自己的机构呢?来看看下面小编为大家介绍的找Java培训机构有哪些评判标准? 找Java培训机构有哪些评判标准? 1.师资力量的标准 我…

Josephus问题
目的:练习下单链表和指针 (OS 10.7 Xcode 4.2) 代码如下: 1 #include <stdio.h>2 #include <stdlib.h>3 4 typedef struct lnode5 {6 int data;7 struct lnode *next; 8 }lnode;9 10 int main(void) 11 …
Datawhale组队学习周报(第017周)
本周(05月31日~06月06日),第 25 期组队学习一共有 3 门开源课程,共组建了 3 个学习群,参与的学习者有 292 人,其中 web开发入门教程 已经结营,另外两门课程也在结营筹划中。 第 26 期组队学习也…

给一个ul列表中点击到的li赋予样式
2019独角兽企业重金招聘Python工程师标准>>> 效果如下,点那个那个获取样式,之前已经有样式的取消。 代码如下,我是在菜鸟教程上在线编辑的,所以就这样喽~ if判断不加也行 <!DOCTYPE html> <html> <head> <…

参加过java培训机构的学员如何找出路
java技术在互联网行业的发展,引起了越来越多人的关注,市面上的java培训机构也不计其数,很多人都比较想知道参加过java培训机构的学员如何找出路?对于这个问题,我们来看看下面的详细介绍就知道了。 参加过java培训机构的学员如何找…

pku The Windy's KM最小权匹配 or 最小费用最大流
http://poj.org/problem?id3686 题意: 给定n个玩具,有m个车间,给出每个玩具在每个车间的加工所需的时间mat[i][j]表示第i个玩具在第j个车间加工所需的时间,规顶只有第i个玩具在j车间完成时第j车间才能接受其他玩具来生产。求加工…

react按需加载(getComponent优美写法),并指定输出模块名称解决缓存(getComponent与chunkFilename)...
react配合webpack进行按需加载的方法很简单,Route的component改为getComponent,组件用require.ensure的方式获取,并在webpack中配置chunkFilename。const chooseProducts (location, cb) > { require.ensure([], require > { cb(null,…

【青少年编程】【二级】绘制方形螺旋
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 微信后台回复“资料下载”可获取以往学习的材料(视频、代码、文档&…
软件测试的发展空间大吗
软件测试的发展空间大吗?很多人都非常关心这个问题,软件测试在互联网行业的发展空间是非常大的,学习软件测试技术并不难,只要经过系统的软件测试培训都是可以学会的,下面来看看详细的介绍。 软件测试的发展空间大吗 早期…

vim windows linux文件格式转换
vim windows linux文件格式转换 set ff? #显示当前文件格式set ffunix #设置成unix格式set ffdos #设置成dos格式posted on 2012-11-02 09:43 一颗卤蛋 阅读(...) 评论(...) 编辑 收藏 转载于:https://www.cnblogs.com/lyroge/archive/2012/11/02/2750689.html

NCEPU:线下组队学习周报(009)
线下组队学习 经过一段时间的准备,我们组织的线下组队学习逐步进入正轨。欢迎华北电力大学保定校区的伙伴加入进来大家一起学习一起成长。 我们开展组队学习的内容为: (1)周志华的《机器学习》(西瓜书) …

零基础学java培训怎么选择学校
java技术在互联网行业的快速发展,引起了很多人的关注,大家都想通过学习java技术来加入到这个行业,那么零基础学java培训怎么选择学校呢?如今市面上的java培训机构这么多,下面小编就来为大家详细的介绍一下吧。 零基础学java培训怎…
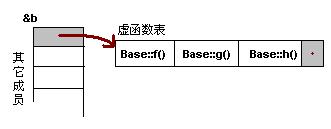
C++对象的内存布局1---基础篇----C++ 虚函数表解析
[-] 前言虚函数表一般继承(无虚函数覆盖)一般继承(有虚函数覆盖)多重继承(无虚函数覆盖)多重继承(有虚函数覆盖)安全性结束语附录一:VC中查看虚函数表附录 二:…

iOS开发 关于启动页和停留时间的设置
引言: 在开发一款商业App时,我们大都会为我们的App设置一个启动页。 苹果官方对于iOS启动页的设计说明: 为了增强应用程序启动时的用户体验,您应该提供一个启动图像。启动图像与应用程序的首屏幕看起来非常相似。 当用户在主屏幕上点击您的应…

web前端培训:CSS中单行文本溢出显示省略号的方法
CSS中单行文本溢出显示省略号的方法你知道吗?在web前端技术学习中,这个问题其实是属于老生常谈了,因为css单行文本的应用是非常频繁的,比如网站最基本的文章列表,标题会很长,而显示列表的区域宽度却没有这么宽&#x…
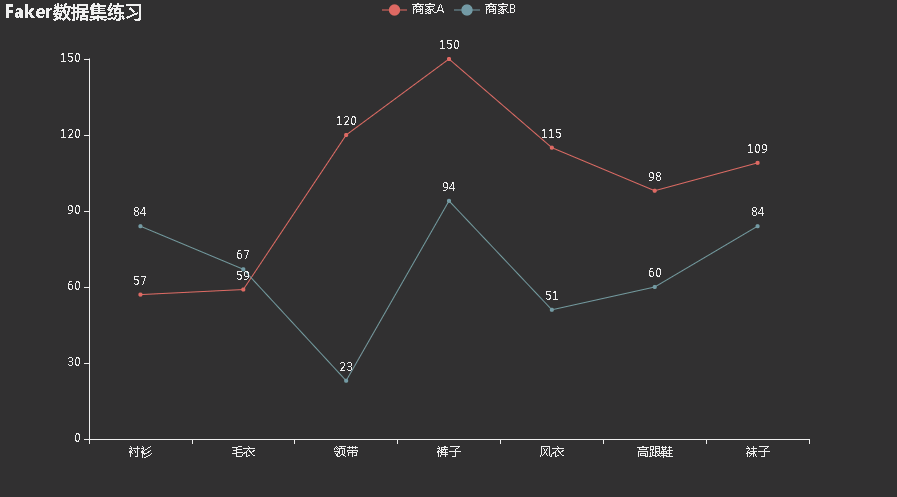
如何使用pyecharts中自带的数据集?
如何使用 pyecharts 中自带的数据集? 我们在学习pyehcarts绘图的过程中,需要一些练习的数据。 pyecharts为我们提供了这样的数据集 – Faker,存储于 faker.py 文件中。 下面,我们就来详细介绍一下。 1. Faker中包含的数据集 …
