当前位置： 首页 > 编程日记 > 正文

led伏安特性实验误差分析_检测实验室误差分析知识汇编

编程日记 2024-09-19 03:50:00

60aea13e989a38da56a79d67f75fb451.png

2019-12-20 09:56:10 来源: 检测实验室误差分析知识汇编-检测家

第一部分 误差理论简介

在日常检测工作中，我们虽然有最好的检验方法、有检定合格的仪器设备、有满足检验要求的环境条件和熟悉检验工作的操作人员，但是，得到的检验结果却往往不可能是绝对准确的，即使是同一检测人员对同一检测样品、对同一项目的检测，其结果也不会完全一样，总会产生这样或那样的差别，也就是说，任何物理量的测定，都不可能是绝对准确的，在测得值与真实值之间总是或多或少的存在着差别，这就是误差。

误差是客观存在的，用它可以衡量检测结果的准确度，误差越小，检测结果的准确度越高。

一 术语和定义

1准确度

准确度指，检测结果与真实值之间相符合的程度。(检测结果与真实值之间差别越小，则分析检验结果的准确度越高)

2 精密度

精密度指，在重复检测中，各次检测结果之间彼此的符合程度。(各次检测结果之间越接近，则说明分析检测结果的精密度越高)

3 重复性

重复性指，在相同测量条件下，对同一被测量进行连续、多次测量所得结果之间的一致性。

重复性条件包括：相同的测量程序、相同的测量者、相同的条件下，使用相同的测量仪器设备，在短时间内进行的重复性测量。

4 再现性(复现性)

在改变测量条件下，同一被测量的测定结果之间的一致性。

改变条件包括：测量原理、测量方法、测量人、参考测量标准、测量地点、测量条件以及测量时间等。

如，实验室资质认定现场操作考核的方法之一：样品复测即是样品再现性(复现性)的一种考核、样品复测包括对盲样(即标准样品)的检测，也可以是对检验过的样品、在有效期内的再检测。或是原检测人员或是重新再安排检测人员。※ 通常再现性或复现性好，意味着精密度高。精密度是保证准确度的先决条件，没有良好的精密度就不可能有高的的准确度，但精密度高准确度不一定高;反之，准确度高，精密度必然好。

二 误差的种类、来源和消除

根据误差的来源和性质，误差可以分为以下几种：

1 系统误差(又称规律误差)

1.1系统误差的定义

※ 系统误差是指，在偏离检测条件下，按某个规律变化的误差。

※ 系统误差是指，同一量的多次测量过程中，保持恒定或可以预知的方式变化的测量误差。

1.2 系统误差的特点

系统误差又称可测量误差，它是由检测过程中某些经常性原因引起的，再重复测定中会重复出现，它对检测结果的影响是比较固定的。

1.3系统误差的主要来源

a)方法误差

主要由于检测方法本身存在的缺陷引起的。如重量法检测中，检测物有少量分解或吸附了某些杂质、滴定分析中，反应进行的不完全、等当点和滴定终点不一致等;

b)仪器误差

由仪器设备精密度不够，引起的的误差。如天平(特别是电子天平，在0.1-0.9mg之间)、砝码、容量瓶等;

C)试剂误差

试剂的纯度不够、蒸馏水中含的杂质，都会引起检测结果的偏高或偏低;

d)操作误差

由试验验人员操作不当、不规范所引起的的误差。如，有的检验人员对颜色观察不敏感，明明已到等当点、颜色已发生突变，可他却看不出来;或在容量分析滴定读数时，读数时间、读数方法都不正确，按个人习惯而进行的操作。

1.4 系统误差的消除

a)对照试验

即用可靠的分析方法对照、用已知结果的标准试样对照(包括标准加入法)，或由不同的实验室、不同的分析人员进行对照等。(实验室资质认定要求做比对计划，如人员比对、样品复测及实验室之间的比对等都属于比对试验)。

b)空白试验

即在没有试样存在的情况下，按照标准检测方法的同样条件和操作步骤进行试验，所得的结果值为空白值，最终，用被测样品的检验结果减去空白值，即可得到比较准确的检测结果。(即实测结果=样品结果-空白值)(再例：重量法中的空白坩埚)。

c)校正试验

即对仪器设备和检验方法进行校正，以校正值的方式，消除系统误差。

被测样品的含量 = 样品的检测结果 × 标样含量/标样检测结果

公式中：标样含量/标样检测结果 — 即校正系数K

例题：若样品的检测结果为5.24，为验证结果的准确性，检测时带一标准样品，已知标准样品含量为1.00，则检测的结果可能出现三种情况：

a)检测结果 > 1.00 假设标样(标物)检测结果为：1.05

b)检测结果 = 1.00 假设标样(标物)检测结果为：1.00

c)检测结果 < 1.00 假设标样(标物)检测结果为：0.95

校正系数K分别为：

a)校正系数为：K = 1.00÷1.05 = 0.95

(检测结果>标准值，则校正系数<1)

b)校正系数为：K = 1.00÷1.00 = 1.00

(检测结果 = 标准值，则校正系数=1)

c)校正系数为：K = 1.00÷0.95 = 1.05

(检测结果

通过校正后，其真实结果应分别为：

a)5.24 ×0.95 = 4.978 ≈ 4.98

(点评：∵ 标样检测结果高于标样明示值，则说明被检样品检测结果也同样偏高，∴为了接近真值，用<1的校正系数进行较正，其结果肯定比原检测值低)

b)5.24 ×1.00 = 5.240 = 5.24

c) 5.24 ×1.05 = 5.502 ≈ 5.50

(点评：∵ 标样检测结果低于标样明示值，则说明被检样品检测结果也同样偏低，∴为了接近真值，用>1的校正系数进行较正，其结果肯定比原检测值高)

【检测结果的校正非常重要，特别是在检测结果的临界值时，加入了校正系数后，结果的判定可能由合格→不合格，也可能由不合格→合格两种完全不同的结论，尤其是对批量产品的判定有着更重大的意义】

2 误差偶然(随机误差、不定误差)

2.1误差偶然(也称随机误差、不定误差)定义

偶然误差指，由于在测定过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差。

2.2 误差偶然(随机误差、不定误差)特点

误差偶然(随机误差、不定误差)特点就个体而言是不确定的，产生的的这种误差的原因是不固定的，它的来源往往也一时难以察觉，可能是由于测定过程中外界的偶然波动、仪器设备及检测分析人员某些微小变化等所引起的，误差的绝对值和符号是可变的，检测结果时大时小、时正时负，带有偶然性。但当进行很多次重复测定时，

就会发现，误差偶然(随机误差、不定误差)具有统计规律性，即服从于正态分布。

如果用置信区间〔-△、△〕，来限制这条曲线(因为我们不可将试验无限次的做下去，即使做得再多，检测结果的误差愈来愈接近于零，但永远也不会等于零)，这样得到截尾正态分布，该正态分布图较好地描述了符合该类分布的偶然误差(随机误差，不定误差)出现的客观规律，且具有以下的基本性质(偶然误差的四性)。

a)单峰性：绝对直小的误差比绝对值大的误差，出现的机会多得多(±1σ占68.3﹪)

b)对称性：绝对值相等的正、负误差出现的概率相等;

c)有界性：在一定条件下，有限次的检测中，偶然误差的绝对值不会超出一定的界限;

d)抵偿性：相同条件下，对同一量进行检测，其偶然误差的平均值，随着测量次数的无限增加，而趋于零。

【抵偿性是偶然误差最本质的统计特性，凡有抵偿性的误差都可以按偶然误差处理】。

显然，从误差的曲线本身就提供了决定了这类误差的理论根据，即用在相同条件下的一系列测量数值的算术平均值来表示分析结果，

这样的平均值是比较可靠的。但，在实际工作中，进行大量的、无限次的测定显然是不真实的。因而，必须根据实际情况、根据对检测结果要求的不同，采取适当的检测次数。

采用数理统计方法以证明：

标准偏差在±1σ内的检测结果，占全部结果的68.3﹪;

标准偏差在±2σ内的检测结果，占全部结果的95.5﹪;

准偏差在±3σ内标的检测结果，占全部结果的99.7﹪;

而误差>±3σ内的检测结果，仅占全部结果的0.3﹪;

而且，由正态分布曲线可以看出，σ3 > σ2 > σ1，σ 值愈小，曲线愈陡，偶然误差的分布愈密集，反之，σ 值愈大，曲线愈平坦，偶然误差的分布就愈分散。

3 粗大误差(简称粗差、也称过失误差、疏忽误差)

3.1粗大误差定义：

※ 粗大误差指，在一定测量条件下，测量值明显偏离实际值所形成的误差(亦称离群值)。

※ 粗大误差指，明显超出测定条件下预期的误差，即是明显歪曲检测结果的误差。


https://www.dkcj.cn/info/19355.html

相关文章：

从Qcheck 1.3 不能在不同操作系统上运行问题（chro124、chro342）说开来------

【本文重在技巧学习&#xff0c;授人以鱼&#xff0c;不如授人以渔&#xff01;&#xff01;&#xff01;】 因为公司项目需要对带宽占用进行测试&#xff0c; 最近看电子工业出版社《网络管理工具使用详解》就qcheck 1.3 不能在不同的操作系统之间运行做一个总结。 本文以标题…

编程日记2024/09/19 03:40:00

Spark笔试

1.Spark 的四大组件下面哪个不是 (D ) A.Spark Streaming B Mlib C Graphx D Spark R 2.下面哪个端口不是 spark 自带服务的端口 (C ) A.8080 B.4040 C.8090 D.18080 3.spark 1.4 版本的最大变化 (B ) A spark sql Release 版本 B 引入 Spark R C DataFrame D支持动态资源…

编程日记2024/09/19 03:30:00

秦州：西瓜书 + 南瓜书 吃瓜系列 10. 集成学习（下）

Datawhale南瓜书是经典机器学习教材《机器学习》&#xff08;西瓜书&#xff09;的公式推导解析指南&#xff0c;旨在让在学习西瓜书的过程中&#xff0c;再也没有难推的公式&#xff0c;学好机器学习。 航路开辟者&#xff1a;谢文睿、秦州开源内容&#xff1a;https://githu…

编程日记2024/09/19 03:20:00

iar定义arm版本_IAR Systems发布 IAR Embedded Workbench for ARM新版本

IAR Systems发布IAR Embedded Workbench for ARM嵌入式开发平台最新版本V5.41。相比于之前的版本&#xff0c;新版本软件在支持Cortex-M0上&#xff0c;将代码大小和执行速度这两个重要性能都提高了13%。本文引用地址&#xff1a;http://www.eepw.com.cn/article/106054.htmNXP…

编程日记2024/09/19 03:10:00

UVA10110 Light, more light

链接地址。 分析&#xff1a; 如果n能被a整除&#xff0c;那么一定存在一个b使得a*b n。开关经两次变化相当于没有变化。那么只要看a b的那种特殊情况就OK了。 #include <stdio.h> #include <math.h> #include <stdlib.h>int main(){unsigned n, k;while(s…

编程日记2024/09/19 03:00:00

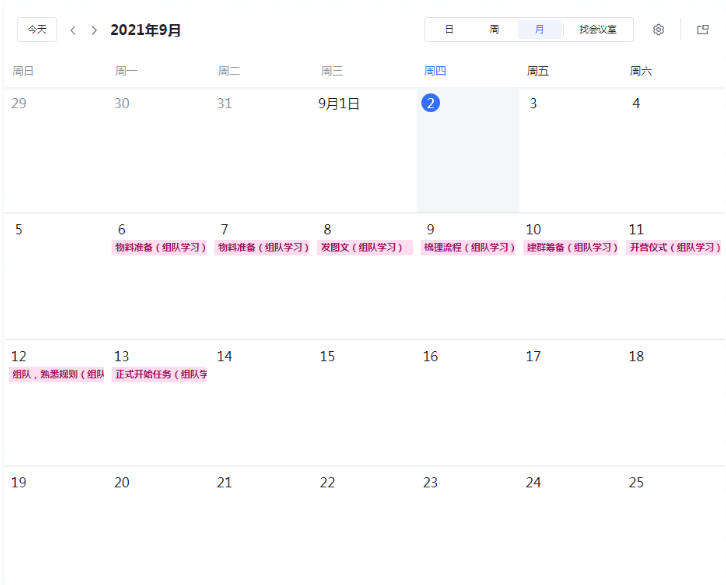
【组队学习】【29期】Datawhale组队学习内容介绍

第29期 Datawhale 组队学习活动马上就要开始啦&#xff01; 本次组队学习的内容为&#xff1a; 编程实践&#xff08;数据可视化&#xff09;计算机视觉自然语言处理之情感分析吃瓜教程——西瓜书南瓜书李宏毅机器学习&#xff08;含深度学习&#xff09;动手学数据分析集成学…

编程日记2024/09/19 02:50:00

json的简单的数据格式

json的简单数据格式 var arr{"obj1":["张三","12","女"],"obj2":["李四","12","女"],"obj3":["王五","12","女"],} var str""; $.each(a…

编程日记2024/09/19 02:40:00

eplise怎么连接数据库_基于手机信令的大数据分析教程（一）数据导入数据库

前言该套教程以一个初学大数据的菜鸟视角&#xff0c;编写数据分析处理的整套流程。写得较为详(luo)细(suo)&#xff0c;希望适用于任何城乡规划大数据的初学者。持续更新中&#xff0c;若有错误&#xff0c;望指正&#xff01;1、任务总纲&#xff08;1&#xff09;职住数据导…

编程日记2024/09/19 02:30:00

反序列化xml

我是.net 菜鸟。 今天学习一下反序列化xml&#xff0c;即将xml文件转换成程序更好识别的对象。 下面来看一个例子。这是一个xml文件。 <xml> <students> <student> <fields> <field value"name"><field> <field value"i…

编程日记2024/09/19 02:20:00

【青少年编程】【三级】小鸡吃虫

「青少年编程竞赛交流群」已成立&#xff08;适合6至18周岁的青少年&#xff09;&#xff0c;公众号后台回复【Scratch】或【Python】&#xff0c;即可进入。如果加入了之前的社群不需要重复加入。 微信后台回复“资料下载”可获取以往学习的材料&#xff08;视频、代码、文档&…

编程日记2024/09/19 02:10:00

Android拍照得到全尺寸图片并进行压缩/拍照或者图库选择 压缩后 图片 上传

http://www.jb51.net/article/77223.htm https://www.cnblogs.com/breeze1988/p/4019510.html

编程日记2024/09/19 02:00:00

display会影响canvas吗_多动症会影响智商吗？

小智&#xff08;化名&#xff09;小的时候非常皮&#xff0c;上学了也不老实&#xff0c;学习成绩还很差&#xff0c;一直是倒数&#xff0c;还有人说他智商低。父母带他到医院检查&#xff0c;一切都正常&#xff0c;智商也没问题。直到最近他被检查出多动症&#xff0c;小智…

编程日记2024/09/19 01:50:00

SQL Server 数据库清除日志的方法

方法一&#xff1a; 1、打开查询分析器&#xff0c;输入命令 BACKUP LOG database_name WITH NO_LOG 2、再打开企业管理器--右键要压缩的数据库--所有任务--收缩数据库--收缩文件--选择日志文件--在收缩方式里选择收缩至xxm,这里会给出一个允许收缩到的最小m数,直接输入这个数,…

编程日记2024/09/19 01:40:00

Axure8.0 网页 or App 鼠标滚动效果

1、index 页下添加一个内联框架&#xff0c;设置好自己想要的尺寸。 2、右键点击该内联框架转换为动态面板&#xff0c;并取消勾选“自动调整为内容尺寸”。 3、双击 “内联框架”选择并双击“state1” 切换到“内联框架的state1”页面&#xff0c;将“内联框架”组件的滚动条设…

编程日记2024/09/19 01:30:00

【组队学习】【29期】1. 编程实践（数据可视化）

1. 编程实践&#xff08;数据可视化&#xff09; 航路开辟者&#xff1a;杨剑砺、杨煜、耿远昊、李运佳、居凤霞领航员&#xff1a;范佳慧航海士&#xff1a;杨剑砺、伊雪、肖桐、李晴晴、蔡婧旎 基本信息 开源内容&#xff1a;https://github.com/datawhalechina/fantastic…

编程日记2024/09/19 01:20:00

训练不出结果_智能训练仪：专业化智能防控近视训练设备

视觉训练精准化&#xff0c;近视防控效果佳智能训练仪小百科 智能训练仪是一款近视防控全功能智能康复设备&#xff0c;一机集成十大视功能康复模块&#xff0c;针对各种视功能异常引发的儿童及青少年假…

编程日记2024/09/19 01:10:00

贪心算法之最优装载

贪心算法通过一系列的选择来得到问题的解。它所做的每一个选择都是当前状态下局部最好选择。从许多的贪心算法求解的问题可以看到可用贪心算法求解的问题一般具有两个重要的性质&#xff1a;贪心选择性质和最优子结构性质。 1、贪心选择性质 贪心选择性质是 指所求问题的整体最…

编程日记2024/09/19 01:00:00

百度认为什么样的网站更有抓取和收录价值

百度认为什么样的网站更有抓取和收录价值 百度认为什么样的网站更有抓取和收录价值呢?我们从下面几个方面简单介绍.鉴于技术保密以及网站运营的差异等其他原因&#xff0c;以下内容仅供站长参考&#xff0c;具体的收录策略包括但不仅限于所述内容。 第一方面&#xff1a;网站创…

编程日记2024/09/19 00:50:00

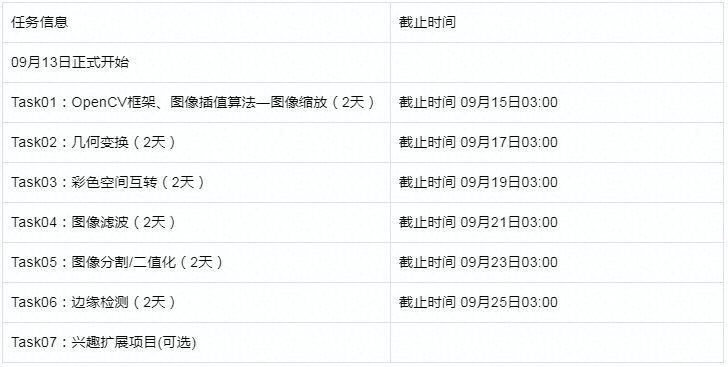
【组队学习】【29期】2. 计算机视觉

2. 计算机视觉 航路开辟者&#xff1a;王程伟、任乔牧、张强、李芝翔领航员&#xff1a;杜蕊航海士&#xff1a;王程伟、任乔牧、张强、李芝翔 基本信息 开源内容&#xff1a;https://github.com/datawhalechina/team-learning-cv/tree/master/ImageProcessingFundamentals内…

编程日记2024/09/19 00:40:00

python 列表维度_如何输出python中list的维度

python中输出list的维度可以使用numpy来实现：import numpy as np a = [[1,2],[3,4]] print(np.array(a).shape) 扩展： reshape&resize&shape改变数组维度 reshape函数：不改变原数组维度，有返回值 resize函数：直接改变原数组维度，无返回值 shape属性：直接改变原数…

编程日记2024/09/19 00:30:00

SWFTools PDF转换为SWF

前言 在iText 制作PDF这篇博文中只是简单的介绍了如何制作PDF&#xff0c;为了能让PDF在Web页面中显示&#xff0c;我还需要通过SWFTools工具将PDF文件转换为SWF文件&#xff0c;然后通过SWF文件显示在Web网页中&#xff0c;本次主要是实践SWFTools工具的简单使用&#xff0c;可…

编程日记2024/09/19 00:20:00

Springboot 中 Mybatis 的使用

2019独角兽企业重金招聘Python工程师标准>>> 官方文档&#xff1a; Mybatis开发团队为Spring Boot 提供了 MyBatis-Spring-Boot-Starter 方便使用。 要使用MyBatis-Spring-Boot-Starter模块&#xff0c;只需要在类路径中包含 mybatis-spring-boot-autoconfigure.ja…

编程日记2024/09/19 00:10:00

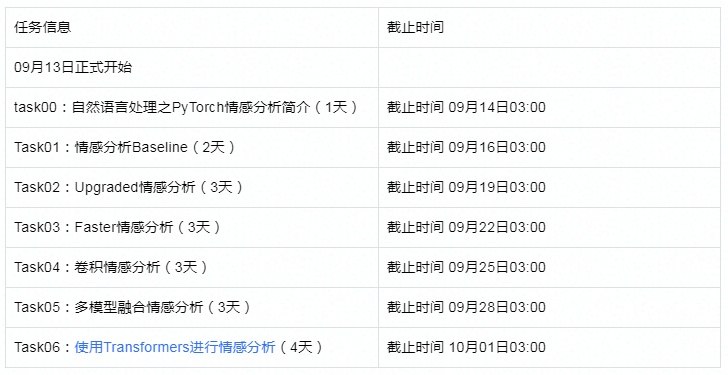
【组队学习】【29期】3. 自然语言处理之情感分析

3. 自然语言处理之情感分析 航路开辟者&#xff1a;芙蕖、戴治旭、陈海顺领航员&#xff1a;初晓宇航海士&#xff1a;芙蕖、戴治旭、陈海顺、汪超 基本信息 开源内容&#xff1a;https://github.com/datawhalechina/team-learning-nlp/tree/master/Emotional_Analysis内容属…

编程日记2024/09/19 00:00:00

cvpr 深度估计_无监督单目视频深度估计中的uncertainty方法(CVPR#x27;20)

Contribution对11种使用uncertainty方法的全面评估深度挖掘uncertainty对depth estimation起到的作用提出一个新颖的self-teaching方法去model uncertainty文中使用的uncertainty estimation分为两个类别&#xff1a;empirical uncertainty estimation和predictive uncertainty…

编程日记2024/09/18 23:50:00

python之CSV文件格式

1、csv文件是以一些以逗号分隔的值 import csv filename "wenjian.csv" with open(filename) as f:reader csv.reader()header next(reader)for index,column in enumerate(header):#enumerate函数获取每个元素的索引及其值print(index,column) 转载于:https://ww…

编程日记2024/09/18 23:40:00

最受欢迎的ASP.NET的CMS下载

http://www.csdn.net/article/2011-11-28/308172 转载于:https://www.cnblogs.com/xuddong/archive/2013/04/08/3071733.html

编程日记2024/09/18 23:30:00

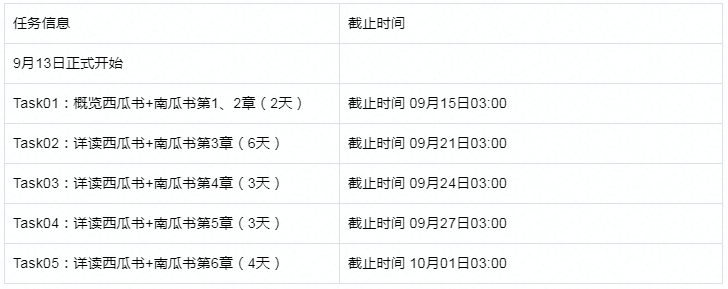
【组队学习】【29期】4. 吃瓜教程——西瓜书+南瓜书

4. 吃瓜教程——西瓜书南瓜书 航路开辟者&#xff1a;谢文睿、秦州领航员&#xff1a;刘琳航海士&#xff1a;谢文睿、秦州 基本信息 开源内容&#xff1a;https://github.com/datawhalechina/pumpkin-bookB 站视频&#xff1a;https://www.bilibili.com/video/BV1Mh411e7VU…

编程日记2024/09/18 23:20:00

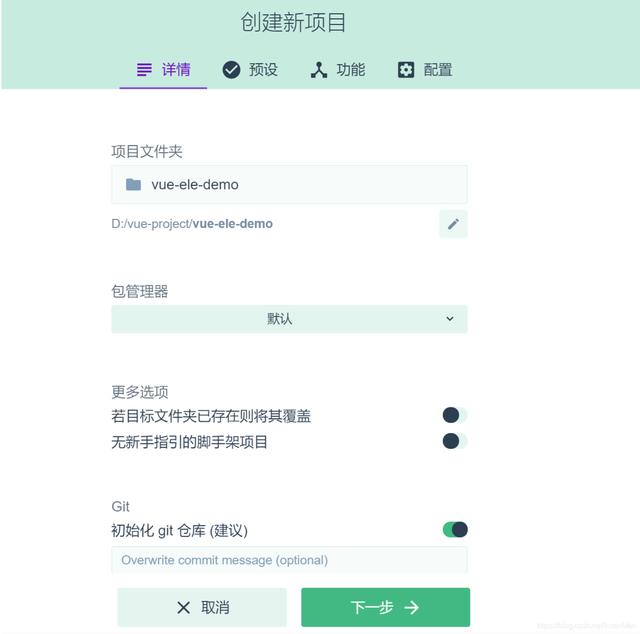
editor修改样式 vue_vue+element-ui项目搭建实战

1.使用vue ui创建vue工程利用vue-cli提供的图形化工具快速搭建vue工程&#xff1a;命令行运行&#xff1a;vue ui工程结构说明build&#xff1a;项目构建webpack(打包器)相关代码config&#xff1a;配置目录&#xff0c;包括端口号等node_modules&#xff1a;npm加载的项目依赖…

编程日记2024/09/18 23:10:00

【IT笔试面试题整理】不用加减乘除做加法

【试题描述】写一个函数&#xff0c;求两个整数的和&#xff0c;要求在函数体内不得使用加减乘除四则运算符合。 基本思路是这样的&#xff1a; int A, B;A&B //看哪几位有进位A^B //不带进位加 考虑二进制加法的过程&#xff0c; 步骤一、A^B&#xff0c;能够得到没有…

编程日记2024/09/18 23:00:00

修改centos7的网卡名

1. 使用命令修改网卡名 cd /etc/sysconfig/network-scripts/ mv ifcfg-ens33 ifcfg-eth0 mv ifcfg-ens34 ifcfg-eth1 2. 修改网卡内容 cat > ifcfg-eth0<<END TYPEEthernet BOOTPROTOnone DEFROUTEyes IPV4_FAILURE_FATALno NAMEeth0 DEVICEeth0 ONBOOTyes IPADDR1…

编程日记2024/09/18 22:50:00