【数学基础】校招算法工程师笔试题
请留言,说出你的解题思路和答案。稍后,我会把参考答案发到留言区。不定期整理相关的问题答案分享。
1、下列矩阵的主元列为()
A=[000111001123]A=\begin{bmatrix}0&0&0&1\\1&1&0&0\\1&1&2&3\end{bmatrix} A=⎣⎡011011002103⎦⎤
- A. 第1列,第4列
- B. 第1列,第2列、第3列
- C. 第3列、第4列
- D. 第1列、第3列、第4列
2、下列线性方程组有解的充要条件是()
{x1−x2=a1x2−x3=a2x3−x4=a3x4−x5=a4x5−x1=a5\left \{ \begin{array}{c} x_1 - x_2 = a_1 \\ x_2 - x_3 = a_2\\ x_3 - x_4 = a_3\\ x_4 - x_5 = a_4\\ x_5 - x_1 = a_5\\ \end{array} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x1−x2=a1x2−x3=a2x3−x4=a3x4−x5=a4x5−x1=a5
- A. a1=0a_1=0a1=0
- B. a1+a2=0a_1 + a_2 = 0a1+a2=0
- C. a1+a2+a3=0a_1 + a_2 + a_3 = 0a1+a2+a3=0
- D. a1+a2+a3+a4+a5=0a_1 + a_2 + a_3 + a_4 + a_5 = 0a1+a2+a3+a4+a5=0
3、如果nnn元非齐次线性方程组系数矩阵AAA的秩小于nnn,则()
- A. 方程组有无穷多解
- B. 方程组有唯一解
- C. 方程组无解
- D. 不能判定解的情况
4、当kkk取()时,可使矩阵R(A)=1R(A)=1R(A)=1。
A=[1−23k−12k−3k−23]A = \begin{bmatrix} 1 & -2 & 3k\\ -1 & 2k & -3\\ k & -2 & 3\\ \end{bmatrix} A=⎣⎡1−1k−22k−23k−33⎦⎤
- A. k=1k=1k=1
- B. k=−2k=-2k=−2
- C. k≠−1,k≠2k\neq-1,k\neq 2k=−1,k=2
- D. k≠1,k≠−2k\neq 1,k\neq -2k=1,k=−2
5、当kkk为()时,下列线性方程组有唯一解。
{x1+x2+kx3=4−x1+kx2+x3=k2x1−x2+2x3=−4\left \{ \begin{array}{c} x_1+x_2+kx_3=4 \\ -x_1+kx_2+x_3=k^2\\ x_1-x_2+2x_3=-4\\ \end{array} \right. ⎩⎨⎧x1+x2+kx3=4−x1+kx2+x3=k2x1−x2+2x3=−4
- A. k=−1k = -1k=−1
- B. k=4k = 4k=4
- C. k≠−1k \neq -1k=−1
- D. k≠−1,k≠4k \neq -1, k \neq 4k=−1,k=4
6、已知矩阵A,BA,BA,B如下所示,AB−BAAB - BAAB−BA为()。
A=[1212−10110],B=[010210021]A = \begin{bmatrix} 1 & 2 & 1\\ 2 & -1& 0\\ 1 & 1 & 0\\ \end{bmatrix}, B = \begin{bmatrix} 0 & 1 & 0\\ 2 & 1 & 0\\ 0 & 2 & 1\\ \end{bmatrix} A=⎣⎡1212−11100⎦⎤,B=⎣⎡020112001⎦⎤
- A. [461−200220]\begin{bmatrix}4 & 6 & 1\\-2 & 0 & 0\\2 & 2 & 0\\\end{bmatrix}⎣⎡4−22602100⎦⎤
- B. [2−104325−10]\begin{bmatrix}2 & -1 & 0\\4 & 3 & 2\\5 & -1 & 0\\\end{bmatrix}⎣⎡245−13−1020⎦⎤
- C. [2712−3−2−330]\begin{bmatrix}2 & 7 & 1\\2 & -3 & -2\\-3 & 3 & 0\\\end{bmatrix}⎣⎡22−37−331−20⎦⎤
- D. [261−6−2−2−330]\begin{bmatrix}2 & 6 & 1\\-6 & -2 & -2\\-3 & 3 & 0\\\end{bmatrix}⎣⎡2−6−36−231−20⎦⎤
7、已知矩阵A,P1A,P_1A,P1如下所示,P1AP_1AP1A为()。
A=[123456789],P1=[010100001]A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix}, P_1 = \begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix} A=⎣⎡147258369⎦⎤,P1=⎣⎡010100001⎦⎤
- A. [456123789]\begin{bmatrix}4 & 5 & 6\\1 & 2 & 3\\7 & 8 & 9\\\end{bmatrix}⎣⎡417528639⎦⎤
- B. [456153789]\begin{bmatrix}4 & 5 & 6\\1 & 5 & 3\\7 & 8 & 9\\\end{bmatrix}⎣⎡417558639⎦⎤
- C. [456123769]\begin{bmatrix}4 & 5 & 6\\1 & 2 & 3\\7 & 6 & 9\\\end{bmatrix}⎣⎡417526639⎦⎤
- D. [213546879]\begin{bmatrix}2 & 1 & 3\\5 & 4 & 6\\8 & 7 & 9\\\end{bmatrix}⎣⎡258147369⎦⎤
8、已知矩阵A,P2A,P_2A,P2如下所示,AP2AP_2AP2为()。
A=[123456789],P2=[k00010001]A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix}, P_2 = \begin{bmatrix} k & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} A=⎣⎡147258369⎦⎤,P2=⎣⎡k00010001⎦⎤
- A. [k234567k89]\begin{bmatrix}k & 2 & 3\\4 & 5 & 6\\7k & 8 & 9\\\end{bmatrix}⎣⎡k47k258369⎦⎤
- B. [k2k3k456789]\begin{bmatrix}k & 2k & 3k\\4 & 5 & 6\\7 & 8 & 9\\\end{bmatrix}⎣⎡k472k583k69⎦⎤
- C. [k234k567k89]\begin{bmatrix}k & 2 & 3\\4k & 5 & 6\\7k & 8 & 9\\\end{bmatrix}⎣⎡k4k7k258369⎦⎤
- D. [k234k56789]\begin{bmatrix}k & 2 & 3\\4k & 5 & 6\\7 & 8 & 9\\\end{bmatrix}⎣⎡k4k7258369⎦⎤
9、已知矩阵A,P3A,P_3A,P3如下所示,AP3AP_3AP3为()。
A=[123456789],P3=[100k10001]A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix}, P_3 = \begin{bmatrix} 1 & 0 & 0\\ k & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} A=⎣⎡147258369⎦⎤,P3=⎣⎡1k0010001⎦⎤
- A. [123456789]\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\\\end{bmatrix}⎣⎡147258369⎦⎤
- B. [1+2k234+5k567+9k89]\begin{bmatrix}1+2k & 2 & 3\\4+5k & 5 & 6\\7+9k & 8 & 9\\\end{bmatrix}⎣⎡1+2k4+5k7+9k258369⎦⎤
- C. [1+2k234+5k567+8k89]\begin{bmatrix}1+2k & 2 & 3\\4+5k & 5 & 6\\7+8k & 8 & 9\\\end{bmatrix}⎣⎡1+2k4+5k7+8k258369⎦⎤
- D. [1234+k5+2k6+3k789]\begin{bmatrix}1 & 2 & 3\\4+k & 5+2k & 6+3k\\7 & 8 & 9\\\end{bmatrix}⎣⎡14+k725+2k836+3k9⎦⎤
10、已知矩阵A,BA,BA,B如下所示,BTAB^TABTA为()
A=[221],B=[112]A = \begin{bmatrix} 2 & 2 & 1\\ \end{bmatrix}, B = \begin{bmatrix} 1 & 1 & 2\\ \end{bmatrix} A=[221],B=[112]
- A. [224224112]\begin{bmatrix}2 & 2 & 4\\2 & 2 & 4\\1 & 1 & 2\\\end{bmatrix}⎣⎡221221442⎦⎤
- B. 6
- C. [221221442]\begin{bmatrix}2 & 2 & 1\\2 & 2 & 1\\4 & 4 & 2\\\end{bmatrix}⎣⎡224224112⎦⎤
- D. [224112224]\begin{bmatrix}2 & 2 & 4\\1 & 1 & 2\\2 & 2 & 4\\\end{bmatrix}⎣⎡212212424⎦⎤
相关文章:

IOS6.0 应用内直接下载程序 不需跳转AppStore
闲来没事看了篇文章 应用内创建应用商店环境,不跳转AppStore. 先武断的想一句:放屁。然后好奇的进去看看,原来是IOS6.0的新特性,顿感惭愧。研究下 SKStoreProductViewController类是UIViewController的子类, 如果你对view control…

python语言基础汇总
注释 代码中添加注释是一个良好的编程习惯,python语言的注释才用井号#作为注释开头的,可以是任意内容,解释器会忽略掉这部分内容。其他每一行都是语句,当语句以冒号:结尾时,缩进的语句视为代码块。 数据类型 python中有…

docker安装mysql5.7_超详细Docker安装Mysql5.7并进行挂载
1、下载mysql 5.7镜像docker pull mysql:5.72、创建mysql容器并启动docker run -d -p 3306:3306 -e MYSQL_USER"ppx" -e MYSQL_PASSWORD"123456" -e MYSQL_ROOT_PASSWORD"123456" --name mysqltest1 mysql:5.7 --character-set-serverutf8 --col…

SQL查询语句 select 详解
查询select: 1。单表查询 2。多表查询 3。嵌套查询分类 1)单表查询 2)多表查询 A.连接查询 B.子查询 ①一般子查询 ②相关子查询***************************************SQL查询语句《一》:单表查询1.查询全部记录:select * from…

【青少年编程】【蓝桥杯】绘制扇子
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

centos 7.2 yum mysql_20191209_Centos7.2使用yum安装mysql
1. 下载mysql的rpm包[rootizwz91qnvovd6suufon1ccz ~]# wget http://dev.mysql.com/get/mysql57-community-release-el7-7.noarch.rpm2. 安装rpm包[rootizwz91qnvovd6suufon1ccz ~]# yum localinstall -y mysql57-community-release-el7-7.noarch.rpm3. 安装mysql 5.7[rootizwz…

activity 的属性android:taskAffinity和android:allowTaskReparenting
1.清单文件中,activity 的属性 android:allowTaskReparenting 这个属性用于设定Activity能够从启动它的任务中转移到另一个与启动它的任务有亲缘关系的任务中,转移时机是在这个有亲缘关系的任务被带到前台的时候。如果设置了true,则能够转移…

数据库内核月报 - 2017年12月
#01 MySQL 引擎特性 InnoDB 事务系统#02 MySQL 引擎特性 Innodb 锁子系统浅析#03 MySQL 特性分析 LOGICAL_CLOCK 并行复制原理及实现分析#04 PgSQL 源码分析 AutoVacuum机制之autovacuum launcher#05 MSSQL 最佳实践 SQL Server备份策略#06 MySQL 最佳实践 一个“异…
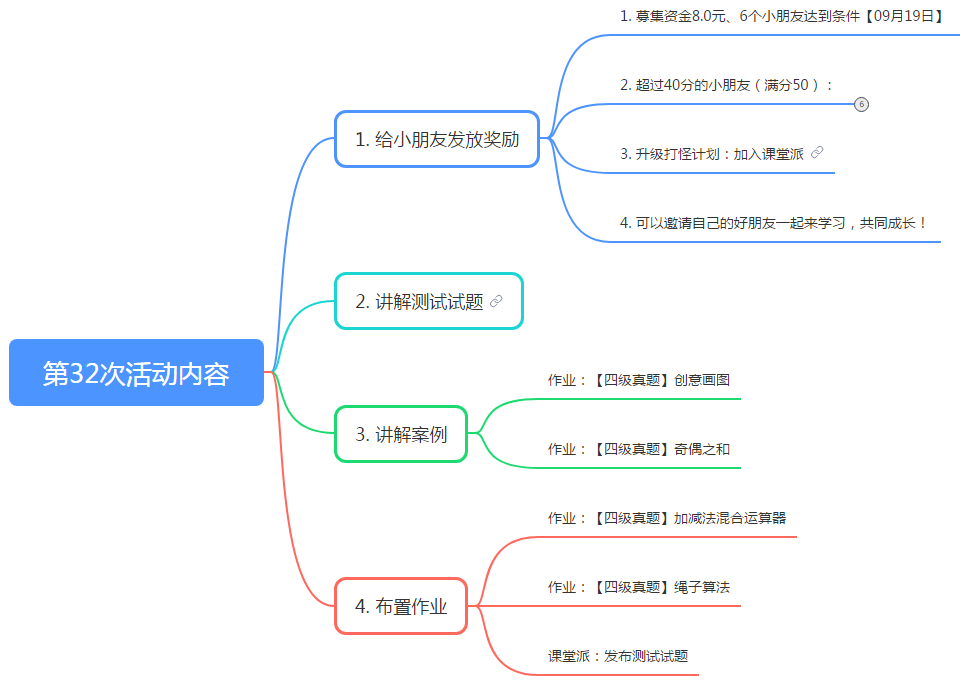
【青少年编程(第32周)】李老师太给力了!
2021年10月03日(周日)晚20:00我们在青少年编程竞赛交流群开展了第三十二期直播活动。我们直播活动的主要内容如下: 首先,我们奖励了上周测试超过40分的小朋友。 其次,我们讲解了上次测试中小朋友们做错的题目Scratch青…
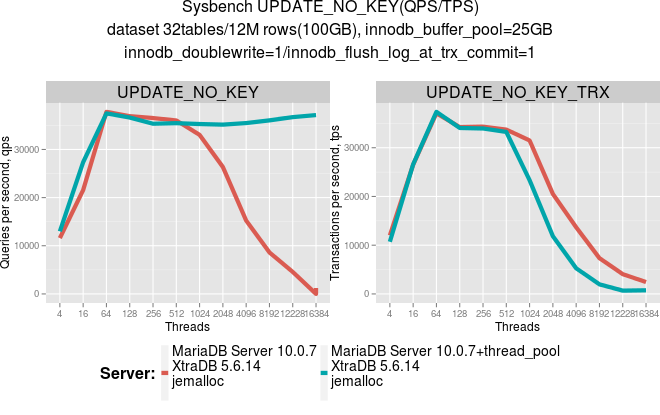
mysql5.6 thread pool_mysql5.6 thread pool
从percona 的压测来看,确实很牛笔啊。提升很大。http://www.mysqlperformanceblog.com/2014/01/29/percona-server-thread-pool-improvements/当然,他指出目前mysql5.6 有2套thread pool ,一套是mysql企业版里面的,另外一套是mari…
选项选择Windows XP系统安装MySQL5.5.28图解
本文纯属个人见解,是对前面学习的总结,如有描述不正确的地方还请高手指正~ Windows XP系统安装MySQL5.5.28图解 MySQL数据库的安装一共分为两个部分:数据库的安装和数据库的配置。 一、MySQL数据库的安装 1、双击下载的MySQL安装文件…
荣耀:想成功要敢于推翻重来
1月底,荣耀总裁赵明接受了吴晓波的采访。在采访中,赵明在谈到手机行业的未来,以及手机企业该如何应对时,说“做企业一定要有消灭自己的勇气,才能够在一波一波的浪潮当中活下来”。事实上,正是因为有着这种敢…
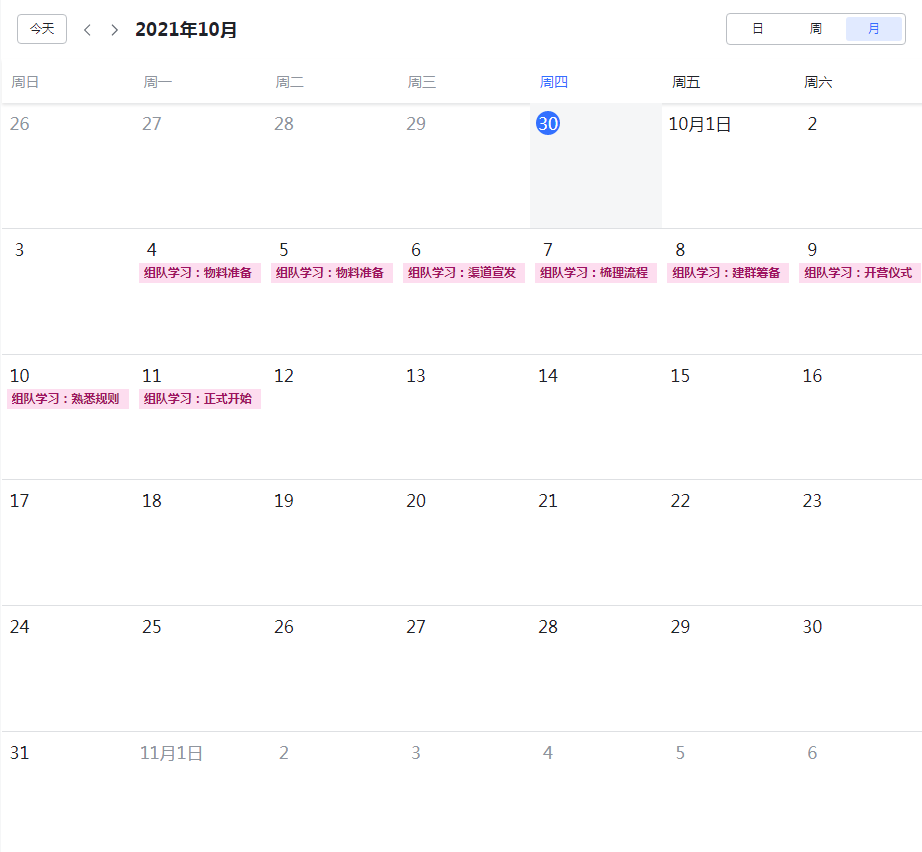
【组队学习】十月组队学习内容详情!(第30期)
第30期 Datawhale 组队学习活动马上就要开始啦! 本次组队学习的内容为: 吃瓜教程——西瓜书南瓜书李宏毅机器学习(含深度学习)深入浅出Pytorch时间序列分析机器学习数学基础树模型与集成学习CV中的Transformer青少年编程…

php mysql ajax日历记事本_php+mysql+jquery日历签到
在网站开发过程中我们会经常用到签到功能来奖励用户积分,或者做一些其他活动。这次项目开发过程中做了日历签到,因为没有经验所有走了很多弯路,再次记录过程和步骤。1.日历签到样式:2.本次签到只记录本月签到数,想要查…

转【红帽GFS集群文件系统配置指南】
本节中将简单的介绍下RedHat的集群文件系统GFS的配置,集群文件系统同普通的文件系统,例如:ext3,ufs,ntfs不一样,集群文件系统采用分布式锁管理,可以实现多个节点同时读写文件。主流的集群文件主要有IBM的GP…
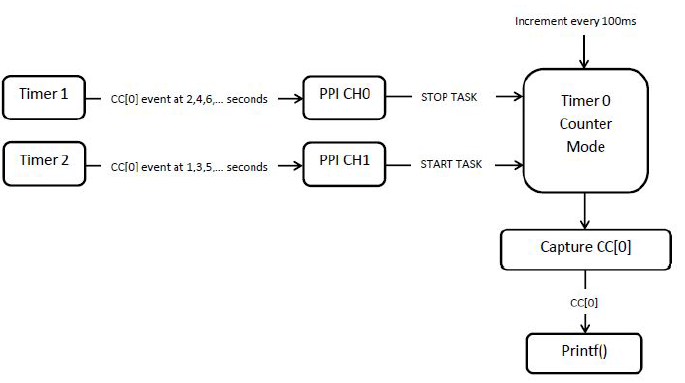
[nRF51822] 8、基础实验代码解析大全 · 实验11 - PPI
前一篇分析了前十个基础实验的代码,从这里开始分析后十个~ 一、PPI原理: PPI(Programmable Peripheral Interconnect),中文翻译为可编程外设互连。 在nRF51822 内部设置了PPI 方式,可以通过任务和事件让不同外设之间进行互连&…
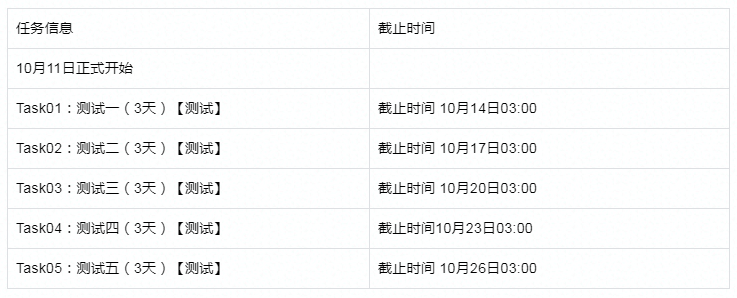
【组队学习】【第30期】青少年编程(Scratch 三级)
小朋友们大家好,我是本次组队学习的领航员-马燕鹏,欢迎大家参加《青少年编程(Scratch 三级)》航海活动。 今天的开营有两大环节: 1、「活动介绍」介绍我们这个活动的整体设计框架。2、「规则介绍」介绍我们本次活动要…

linux resin mysql_Linux下Resin JSP MySQL的安装和配置-2
如果有,陆续(2)编辑httpd.conf# vi /usr/local/apache2/conf/httpd.conf找到ResinConfigServer localhost 6802确信其内容为:LoadModule caucho_module /usr/local/apache2/modules/mod_caucho.soResinConfigServer 192.168.1.109 6802 //即改localhost为你的计算机的实际IPCa…

胡锐锋:组队学习分享(队长)
组队学习分享(队长) 自我介绍 胡锐锋,现为Datawhale成员,目前担任《统计学习方法习题解答》开源项目的负责人,已工作近8年,由大数据平台研发工程师转变成一位项目管理人。我的人生目标是让未来的孩子们少…

[转]解析字符串的方法
解析字符串的方法 char st[]”123.45ab”; 解析这一段字符串,有很多种方法。这里介绍一个在”stdio.h”里面的函数: sscanf(…); 如果你看了如下代码,应该会有所感悟: 1 # include "stdio.h"2 3 int main() {4 char st[]"…

SpringBoot之@EnableConfigurationProperties分析
我们在用SpringBoot进行项目开发的时候,基本上都使用过ConfigurationProperties这个注解,我们在之前的文章中也说过ConfigurationPropertiesBindingPostProcessor会对标注ConfigurationProperties注解的Bean进行属性值的配置,但是我们之前没有…

mysql 自动管理内存_MySQL内存管理,内存分配器和操作系统
导读作者:Sveta Smirnova翻译:郑志江校对:徐晨亮原文 :MySQL Memory Management, Memory Allocators and Operating System本文涉及链接在文末展示当用户使用任何软件(包括MySQL)碰到内存问题时,我们第一反应就是内存泄…

采集音频和摄像头视频并实时H264编码及AAC编码
0. 前言 我在前两篇文章中写了DirectShow捕获音视频然后生成avi,再进行264编码的方法。那种方法有一些局限性,不适合实时性质的应用,如:视频会议、视频聊天、视频监控等。本文所使用的技术,适用于这种实时性的应用&…

【算法练习】校招研发工程师笔试题
请留言,说出你的解题思路和答案。稍后,我会把参考答案发到留言区。不定期整理相关的问题答案分享。 01、下面对于线性表的叙述中,不正确的是()。 (A)线性表采用顺序存储时,必须占用…

Ubuntu安装tomcat
1.从官网中下载apache-tomcat-**.tar.gz文件 2.在本地文件新建一个文件夹(tomcat),在文件夹中解压压缩包, 不需要使用root: tar -zxvf /home/xcx/下载/apache-tomcat-8.5.11.tar.gz 3.进入解压文件中使用命令,将tomcat中的文件全部设置添加读…

mysql 绑定参数_MySQL 使用 Perl 绑定参数和列
SQL 语句通常是动态构建的,用户提供一些输入,并将其内置到语句中。 程序员每次处理用户的输入时都必须谨慎。 它具有一些严重的安全隐患。 动态构建 SQL 语句的推荐方法是使用参数绑定。绑定参数可以防止 SQL 注入程序。 它会自动转义一些特殊字符并允许…

java入门(p1)进入java的世界
浅谈java世界(连载中P1) Java是一门语言,它并不是很难理解的东西,语言是来进行交流的工具,那么它用来跟谁来交互呢,所有的语言都有与其交流的对象,中文也好英文也罢,交流基本的对象应…

python __setattr__ , __getattr__
Python Class 对象或类型通过内置成员 __dict__ 来存储成员信息。 我们还可以通过重载 __getattr__ 和 __setattr__ 来拦截对成员的访问,需要注意的是 __getattr__ 只有在访问不存在的成员时才会被调用。转载于:https://www.cnblogs.com/Huayuan/archive/2013/05/17…

第01章 PyTorch简介和安装 的学习笔记
由于第一章,主要介绍Pytorch的安装,而自己的笔记本已经安装了CPU版本的Pytorch,所以第一章主要是复习了Conda的基本命令并做了5个选择题供大家练习。 课程来源:https://github.com/datawhalechina/thorough-pytorch 1、在Window…

python socket tcp客户端_python网络编程socketserver模块(实现TCP客户端/服务器)
摘录python核心编程socketserver(python3.x版本重新命名)是标准库中的网络编程的高级模块。通过将创建网络客户端和服务器所必须的代码封装起来,简化了模板,为你提供了各种各样的类。除了隐藏了实现细节之外,它督促我们使用类(面向对象的思维…
