【优秀作业】粒子群算法(Python)
粒子群优化算法
一、概述
粒子群优化算法(Particle Swarm Optimization,PSO)的思想来源于对鸟捕食行为的模仿,最初,Reynolds.Heppner 等科学家研究的是鸟类飞行的美学和那些能使鸟群同时突然改变方向,分散,聚集的定律上,这些都依赖于鸟的努力来维持群体中个体间最佳距离来实现同步。而社会生物学家 E.O.Wilson 参考鱼群的社会行为认为从理论上说,在搜寻食物的过程中,尽管食物的分配不可知,群中的个体可以从群中其它个体的发现以及以往的经验中获益。
粒子群从这种模型中得到启发并用于解决优化问题。如果我们把一个优化问题看作是在空中觅食的鸟群,那么粒子群中每个优化问题的潜在解都是搜索空间的一只鸟,称之为“粒子”(Particle),“食物”就是优化问题的最优解。每个粒子都有一个由优化问题决定的适应度用来评价粒子的“好坏”程度,每个粒子还有一个速度决定它们飞翔的方向和距离,它根据自己的飞行经验和同伴的飞行经验来调整自己的飞行。粒子群初始化为一群随机粒子(随机解),然后通过迭代的方式寻找最优解,在每一次的迭代中,粒子通过跟踪两个“极值”来更新自己,第一个是粒子本身所经历过的最好位置,称为个体极值即PbestPbestPbest;另一个是整个群体经历过的最好位置称为全局极值GbestGbestGbest。每个粒子通过上述的两个极值不断更新自己,从而产生新一代的群体。
二、粒子群算法
算法的描述如下:
假设搜索空间是LLL维,并且群体中有NNN个粒子。那么群体中的第iii个粒子可以表示为一个LLL维的向量,Xi=(xi1,xi2,⋯,xiL),i=1,2,⋯,NX_i=(x_{i1},x_{i2},\cdots,x_{iL}),i=1,2,\cdots,NXi=(xi1,xi2,⋯,xiL),i=1,2,⋯,N,即第iii个粒子在LLL维的搜索空间的位置是XiX_iXi,它所经历的“最好”位置记作Pbesti=(pi1,pi2,⋯,piL),i=1,2,⋯,NPbest_i=(p_{i1},p_{i2},\cdots,p_{iL}),i=1,2,\cdots,NPbesti=(pi1,pi2,⋯,piL),i=1,2,⋯,N。粒子的每个位置代表要求的一个潜在解,把它代入目标函数就可以得到它的适应度值,用来评判粒子的“好坏”程度。整个群体迄今为止搜索到的最优位置记作Gbestg=(pg1,pg2,⋯,pgL)Gbest_g=(p_{g1},p_{g2},\cdots,p_{gL})Gbestg=(pg1,pg2,⋯,pgL),ggg是最优粒子位置的索引。
Vit+1=ωVit+c1r1(Pbestit−Xit)+c2r2(Gbestgt−Xit)(1)V_{i}^{t+1}=\omega V_{i}^{t} + c_1 r_1 (Pbest_i^{t}-X_i^{t}) + c_2 r_2 (Gbest_g^{t}-X_i^{t}) \tag{1} Vit+1=ωVit+c1r1(Pbestit−Xit)+c2r2(Gbestgt−Xit)(1)
Xit+1=Xit+Vit+1(2)X_{i}^{t+1} = X_{i}^{t} + V_{i}^{t+1} \tag{2} Xit+1=Xit+Vit+1(2)
ω\omegaω为惯性权重(inertia weight),PbestitPbest_i^{t}Pbestit为第iii个粒子到第ttt代为止搜索到的历史最优解,GbestgtGbest_g^{t}Gbestgt为整个粒子群到目前为止搜索到的最优解,XitX_i^{t}Xit,VitV_i^{t}Vit分别是第iii个粒子当前的位置和飞行速度,c1,c2c_1,c_2c1,c2为非负的常数,称为加速度因子,r1,r2r_1,r_2r1,r2是[0,1][0,1][0,1]之间的随机数。
公式由三部分组成,第一部分是粒子当前的速度,表明了粒子当前的状态;第二部分是认知部分(Cognition Modal),表示粒子本身的思考(c1c_1c1也称为自身认知系数);第三部分是社会认知部分(Social Modal),表示粒子间的信息共享(c2c_2c2为社会认知系数)。
参数的选择:
粒子数目一般取30~50,参数c1,c2c_1,c_2c1,c2一般取2。适应度函数、粒子的维数和取值范围要视具体问题而定。问题解的编码方式通常可以采用实数编码。
算法的主要步骤如下:
第一步:对粒子群的随机位置和速度进行初始设定,同时设定迭代次数。
第二步:计算每个粒子的适应度值。
第三步:对每个粒子,将其适应度值与所经历的最好位置PbestiPbest_iPbesti的适应度值进行比较,若较好,则将其作为当前的个体最优位置。
第四步:对每个粒子,将其适应度值与全局所经历的最好位置GbestgGbest_gGbestg的适应度值进行比较,若较好,则将其作为当前的全局最优位置。
第五步:根据公式(1),(2)对粒子的速度和位置进行优化,从而更新粒子位置。
第六步:如未达到结束条件(通常为最大循环数或最小误差要求),则返回第二步。
三、基于粒子群算法的非线性函数寻优
本案例寻优的非线性函数为
y=−c×exp(−0.21n∑i=1nxi2)−exp(1n∑i=1ncos2πxi)+c+ey=-c\times \exp(-0.2\sqrt{\frac{1}{n}\sum_{i=1}^{n}{x_i^2}}) - \exp(\frac{1}{n}\sum_{i=1}^{n}{\cos 2\pi x_i})+c+e y=−c×exp(−0.2n1i=1∑nxi2)−exp(n1i=1∑ncos2πxi)+c+e
当c=20c=20c=20,n=2n=2n=2时,该函数为Ackley函数,函数图形如图1所示。
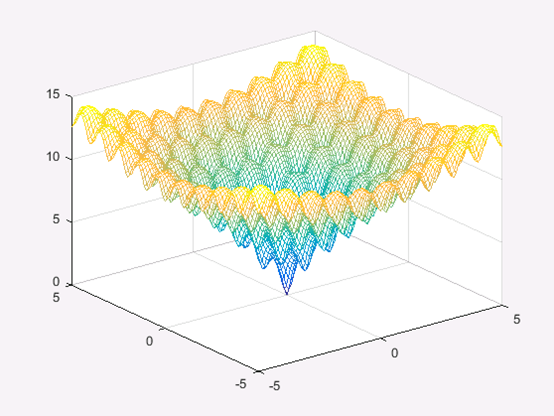
从函数图形可以看出,该函数有很多局部极小值,在(0,0)(0,0)(0,0)处取到全局最小值0。
本案例群体的粒子数为20,每个粒子的维数为2,算法迭代进化次数为100。加速度因子c1=1.4c_1=1.4c1=1.4,c2=1.5c_2=1.5c2=1.5,惯性权重ω=0.1\omega = 0.1ω=0.1。
引入的模块如下:
import numpy as np
import matplotlib.pyplot as plt# 解决中文乱码和负号问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
适应度函数代码如下:
# 函数用于计算粒子适应度值
def funAckley(x):c = 20y = -1.0 * c * np.exp(-0.2 * np.sqrt((x[0] ** 2 + x[1] ** 2) / 2)) \- np.exp((np.cos(2 * np.pi * x[0]) + np.cos(2 * np.pi * x[1])) / 2) \+ c + np.exp(1)return y
PSO算法代码如下:
c1, c2 = 1.4, 1.5 # 加速度因子
maxgen = 100 # 进化次数
sizepop = 20 # 群体规模
w = 0.1 # 惯性权重
Vmax, Vmin = 1, -1 # 速度最大值,最小值
popmax, popmin = 5, -5 # 个体最大值,最小值
pop = np.zeros([sizepop, 2]) # 种群
V = np.zeros([sizepop, 2]) # 速度
fitness = np.zeros(sizepop) # 适应度
trace = np.zeros(maxgen) # 结果# 随机产生一个群体,初始粒子和速度
for i in range(sizepop):pop[i] = 5 * ((-2 * np.random.rand(1, 2) + 1))V[i] = (-2 * np.random.rand(1, 2) + 1)fitness[i] = funAckley(pop[i])# 个体极值和群体极值
bestfitness = np.min(fitness)
bestindex = np.argmin(fitness)
Gbest = pop[bestindex] # 全局最佳
fitnessGbest = bestfitness # 全局最佳适应度值
Pbest = pop.copy() # 个体最佳
fitnessPbest = fitness.copy() # 个体最佳适应度值# 迭代寻优
for i in range(maxgen):for j in range(sizepop):V[j] = w * V[j] + c1 * (-2 * np.random.rand(1, 2) + 1) * (Pbest[j] - pop[j]) \+ c2 * (-2 * np.random.rand(1, 2) + 1) * (Gbest - pop[j]) # 速度更新V[j, V[j] > Vmax] = VmaxV[j, V[j] < Vmin] = Vminpop[j] = pop[j] + V[j] # 群体更新pop[j, pop[j] > popmax] = popmaxpop[j, pop[j] < popmin] = popminfitness[j] = funAckley(pop[j]) # 适应度值if fitness[j] < fitnessPbest[j]:Pbest[j] = pop[j].copy()fitnessPbest[j] = fitness[j]if fitness[j] < fitnessGbest:Gbest = pop[j].copy()fitnessGbest = fitness[j]trace[i] = fitnessGbestprint(Gbest, fitnessGbest)# 结果分析
plt.plot(trace)
plt.title("最优个体适应度")
plt.xlabel("进化代数")
plt.ylabel("适应度")
plt.show()
算法结果如下:
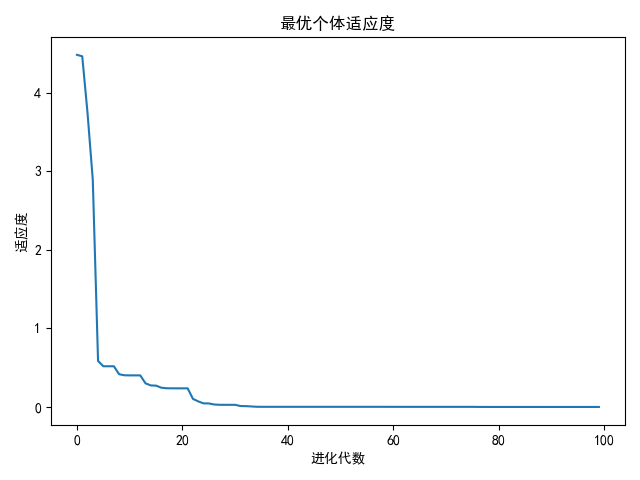
最终得到的个体适应度值为4.660641074893945×10−054.660641074893945\times 10^{-05}4.660641074893945×10−05,对应的粒子位置为(5.49894607×10−06,1.55305207×10−05)(5.49894607\times 10^{-06}, 1.55305207\times 10^{-05})(5.49894607×10−06,1.55305207×10−05),PSO算法寻优得到最优值接近函数实际最优值,说明PSO算法具有较强的函数极值寻优能力。
四、基于自适应变异粒子群算法的非线性函数寻优
本案例寻优的非线性函数(Shubert函数)为
f(x1,x2)=∑i=15icos[(i+1)x1+i]×∑i=15icos[(i+1)x2+i],−10≤x1,x2≤10f(x_1,x_2 )=\sum_{i=1}^{5}{i\cos[(i+1) x_1+i]}\times\sum_{i=1}^{5}{icos[(i+1) x_2+i]},-10\leq x_1,x_2 \leq 10 f(x1,x2)=i=1∑5icos[(i+1)x1+i]×i=1∑5icos[(i+1)x2+i],−10≤x1,x2≤10
该函数图形如图3所示:
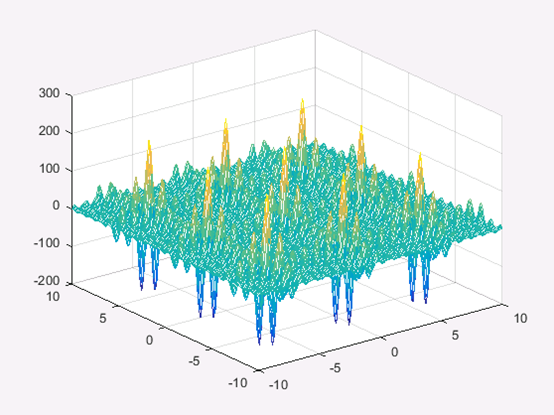
从函数图形可以看出,该函数有很多局部极小值,很难用传统的梯度下降方法进行全局寻优。
自适应变异是借鉴遗传算法中的变异思想,在PSO算法中引入变异操作,即对某些变量以一定的概率重新初始化。变异操作拓展了在迭代中不断缩小的种群搜索空间,使粒子能够跳出先前搜索到的最优值位置,在更大的空间中开展搜索,同时保持了种群多样性,提高算法寻找更优值的可能性。因此,在普通粒子群算法的基础上引入简单变异算子,在粒子每次更新之后,以一定概率重新初始化粒子。
本案例群体的粒子数为50,每个粒子的维数为2,算法迭代进化次数为1000。加速度因子c1=1.4c_1=1.4c1=1.4,c2=1.5c_2=1.5c2=1.5,惯性权重ω=0.8\omega = 0.8ω=0.8。
适应度函数代码如下:
def funShubert(x):h1 = 0h2 = 0for i in range(1, 6):h1 += i * np.cos((i + 1) * x[0] + i)h2 += i * np.cos((i + 1) * x[1] + i)return h1 * h2
自适应变异PSO算法代码如下:
c1, c2 = 1.4, 1.5 # 加速度因子
maxgen = 1000 # 进化次数
sizepop = 50 # 群体规模
w = 0.8 # 惯性权重
Vmax, Vmin = 5, -5 # 速度最大值,最小值
popmax, popmin = 10, -10 # 个体最大值,最小值
pop = np.zeros([sizepop, 2]) # 种群
V = np.zeros([sizepop, 2]) # 速度
fitness = np.zeros(sizepop) # 适应度
trace = np.zeros(maxgen) # 结果# 随机产生一个群体,初始粒子和速度
for i in range(sizepop):pop[i] = 10 * (-2 * np.random.rand(1, 2) + 1)V[i] = 5 * (-2 * np.random.rand(1, 2) + 1)fitness[i] = funShubert(pop[i])# 个体极值和群体极值
bestfitness = np.min(fitness)
bestindex = np.argmin(fitness)
Gbest = pop[bestindex] # 全局最佳
fitnessGbest = bestfitness # 全局最佳适应度值
Pbest = pop.copy() # 个体最佳
fitnessPbest = fitness.copy() # 个体最佳适应度值# 迭代寻优
for i in range(maxgen):for j in range(sizepop):V[j] = w * V[j] + c1 * (-2 * np.random.rand(1, 2) + 1) * (Pbest[j] - pop[j]) \+ c2 * (-2 * np.random.rand(1, 2) + 1) * (Gbest - pop[j]) # 速度更新V[j, V[j] > Vmax] = VmaxV[j, V[j] < Vmin] = Vminpop[j] = pop[j] + V[j] # 群体更新pop[j, pop[j] > popmax] = popmaxpop[j, pop[j] < popmin] = popminif np.random.rand() > 0.9: # 自适应变异pop[j] = 10 * (-2 * np.random.rand(1, 2) + 1)fitness[j] = funShubert(pop[j]) # 适应度值if fitness[j] < fitnessPbest[j]:Pbest[j] = pop[j].copy()fitnessPbest[j] = fitness[j]if fitness[j] < fitnessGbest:Gbest = pop[j].copy()fitnessGbest = fitness[j]trace[i] = fitnessGbestprint(Gbest, fitnessGbest)# 结果分析
plt.plot(trace)
plt.title("最优个体适应度")
plt.xlabel("进化代数")
plt.ylabel("适应度")
plt.show()
算法结果如下:
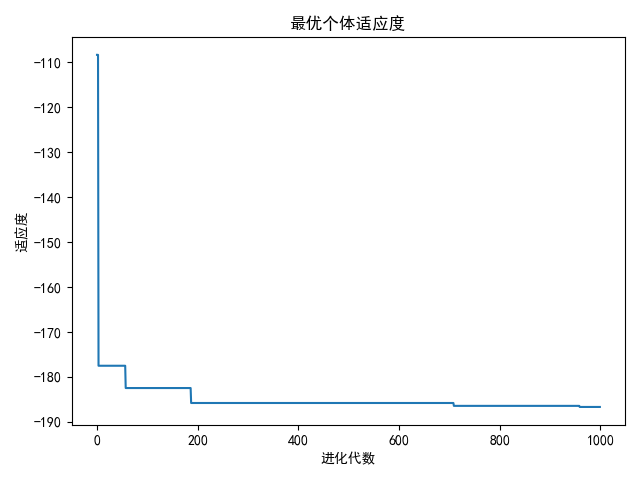
最终得到的个体适应度值为-186.6831831611777,对应的例子位置为(5.4788292,−1.4228858)(5.4788292,-1.4228858)(5.4788292,−1.4228858),自适应变异PSO算法寻优得到最优值接近函数实际最优值,说明该算法具有较强的函数极值寻优能力。
五、补充
惯性权重ω\omegaω体现的是粒子当前速度多大程度上继承先前的速度,Shi.Y最先将惯性权重ω\omegaω引入到PSO算法中,并分析指出一个较大的惯性权值有利于全局搜索,而一个较小的惯性权值则更有利于局部搜索。为了更好地平衡算法的全局搜索与局部搜索能力,其提出了线性递减惯性权重(Linear Decreasing Inertia Weight,LDIW),即
ω(t)=ωstart−(ωstart−ωend)×tTmax\omega(t)=\omega_{start}-(\omega_{start}-\omega_{end})\times\frac{t}{T_{max}} ω(t)=ωstart−(ωstart−ωend)×Tmaxt
式中,ωstart\omega_{start}ωstart为初始惯性权重,ωend\omega_{end}ωend为迭代至最大次数时的惯性权重,ttt为当前迭代次数,TmaxT_maxTmax为最大迭代次数。
一般来说,惯性权重取值为ωstart=0.9\omega_{start}=0.9ωstart=0.9,ωend=0.4\omega_{end}=0.4ωend=0.4时算法性能最好。这样,随着迭代的进行,惯性权重由0.9线性递减至0.4,迭代初期较大的惯性权重使算法保持了较强的全局搜索能力,而迭代后期较小的惯性权值有利于算法进行更精确的局部搜索。
线性惯性权重只是一种经验做法,常用的惯性权重的选择还包括以下几种:
ω(t)=ωstart−(ωstart−ωend)×(tTmax)2\omega(t)=\omega_{start}-(\omega_{start}-\omega_{end})\times(\frac{t}{T_{max}})^2 ω(t)=ωstart−(ωstart−ωend)×(Tmaxt)2
ω(t)=ωstart−(ωstart−ωend)×(2tTmax−(tTmax)2)\omega(t)=\omega_{start}-(\omega_{start}-\omega_{end})\times(\frac{2t}{T_{max}}-(\frac{t}{T_{max}})^2) ω(t)=ωstart−(ωstart−ωend)×(Tmax2t−(Tmaxt)2)
六、练习
求测试函数的最小值,以及最小值点。
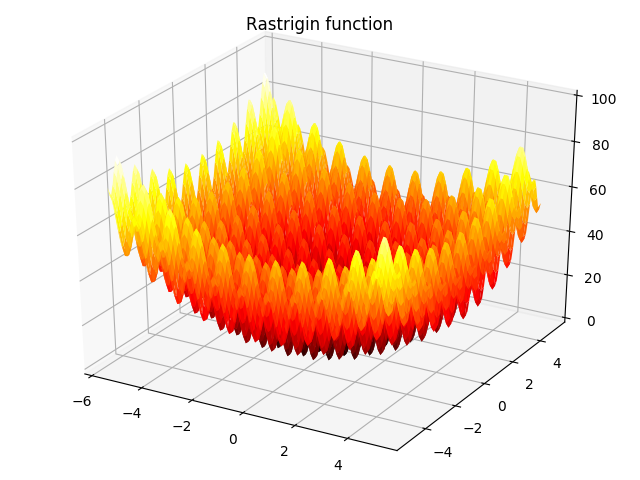
1. Rastrigin function:
f(x)=An+∑i=1n[xi2−Acos(2πxi)],−5.12≤xi≤5.12f(\bm x)=A_n+\sum_{i=1}^{n}{[x_i^2-A\cos (2\pi x_i)]},-5.12\leq x_i\leq 5.12 f(x)=An+i=1∑n[xi2−Acos(2πxi)],−5.12≤xi≤5.12
当A=10,n=2A=10,n=2A=10,n=2时,如下图所示:
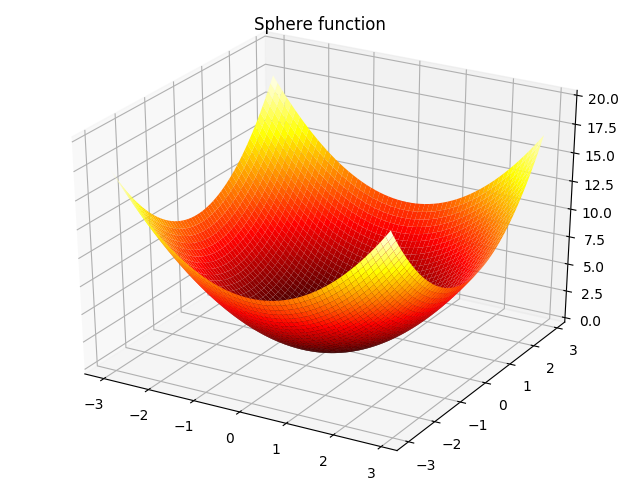
2. Sphere function:
f(x)=∑i=1nxi2,−∞≤xi≤∞f(\bm x) = \sum_{i=1}^{n}{x_i^2},-\infty\leq x_i \leq \infty f(x)=i=1∑nxi2,−∞≤xi≤∞
当n=2n=2n=2时,如下图所示:
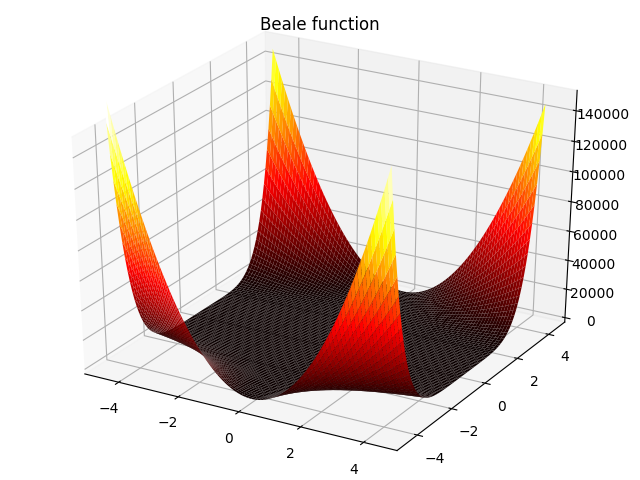
3. Beale function:
f(x,y)=(1.5−x+xy)2+(2.25−x+xy2)2+(2.625−x+xy3)2,−4.5≤x,y≤4.5f(x,y)=(1.5-x+xy)^2+(2.25-x+xy^2)^2+(2.625-x+xy^3)^2,-4.5\leq x,y\leq 4.5 f(x,y)=(1.5−x+xy)2+(2.25−x+xy2)2+(2.625−x+xy3)2,−4.5≤x,y≤4.5
4. Booth function:
f(x,y)=(x+2y−7)2+(2x+y−5)2,−10≤x,y≤10f(x,y)=(x+2y-7)^2+(2x+y-5)^2,-10\leq x,y\leq 10 f(x,y)=(x+2y−7)2+(2x+y−5)2,−10≤x,y≤10
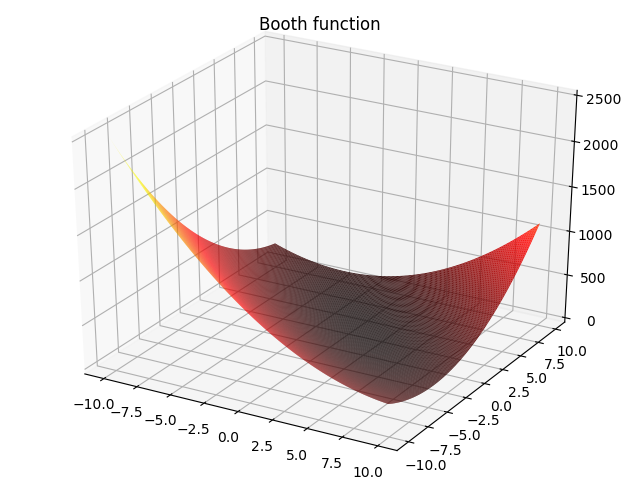
5. Bukin function:
f(x,y)=100∣y−0.01x2∣+0.01∣x+10∣,−15≤x≤−5,−3≤y≤3f(x,y)=100\sqrt{|y-0.01x^2|}+0.01|x+10|,-15\leq x\leq -5,-3\leq y\leq 3 f(x,y)=100∣y−0.01x2∣+0.01∣x+10∣,−15≤x≤−5,−3≤y≤3
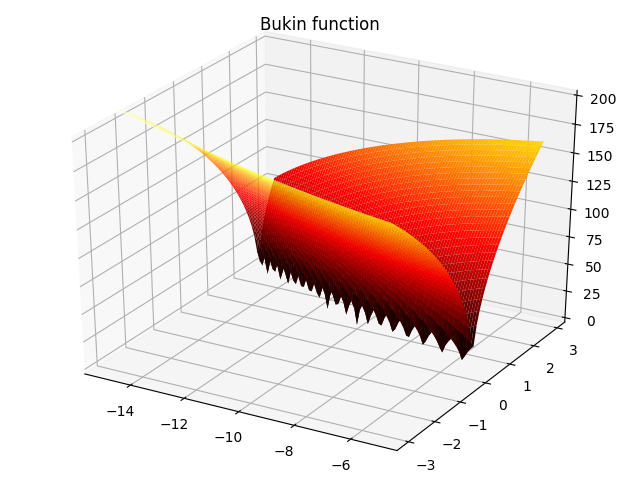
6. three-hump camel function:
f(x,y)=2x2−1.05x4+x66+xy+y2,−5≤x,y≤5f(x,y)=2x^2-1.05x^4+\frac{x^6}{6}+xy+y^2,-5\leq x,y\leq 5 f(x,y)=2x2−1.05x4+6x6+xy+y2,−5≤x,y≤5
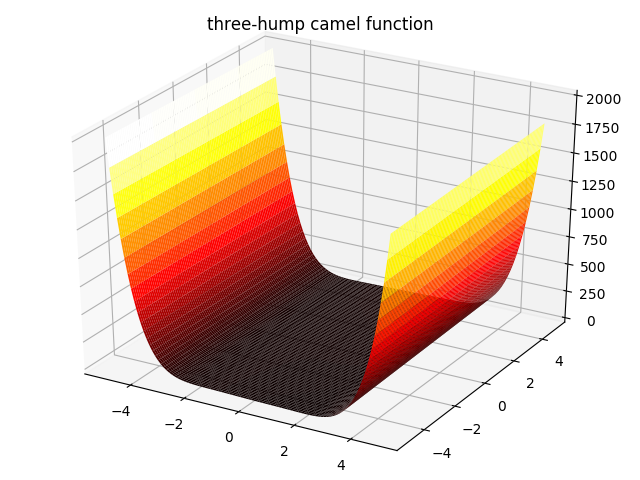
7. Hölder table function:
f(x,y)=−∣sinxcosyexp(∣1−x2+y2π∣)∣,−10≤x,y≤10f(x,y)=-|\sin x \cos y \exp(|1-\frac{\sqrt{x^2+y^2}}{\pi}|)|,-10\leq x,y\leq 10 f(x,y)=−∣sinxcosyexp(∣1−πx2+y2∣)∣,−10≤x,y≤10
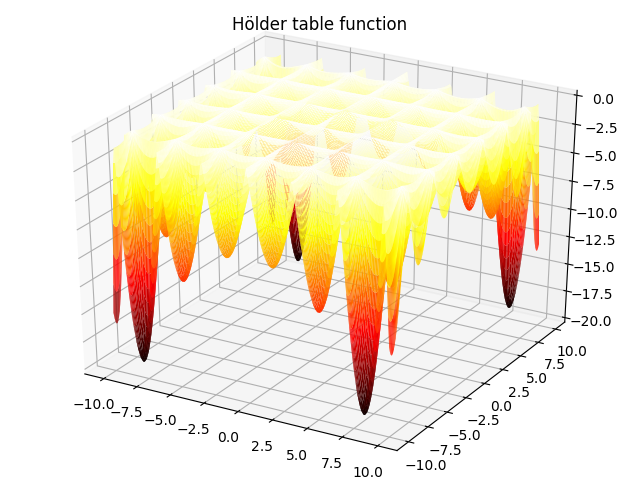
相关文章:

警惕企业中的五种虚假执行力
第一种虚假执行力:无条件服从——只强调员工“服从”,不强调员工的智慧 很多人讲执行力,很喜欢强调员工的无条件服从。这种观念是OEM(代工生产)制造业时代的产物。实际上这是一种基于“规模制造”的虚假执行力,其本质是把人当成了…

真实记录疑似Linux病毒导致服务器 带宽跑满的解决过程
案例描述 由于最近我在重构之前的APP,需要和server端进行数据交互,发现有一个现象,那么就是隔1~2天总会发生获取数据超时的问题,而且必须要重启服务器才能解决。早在之前,我有留意到这个问题,但是由于这个服…
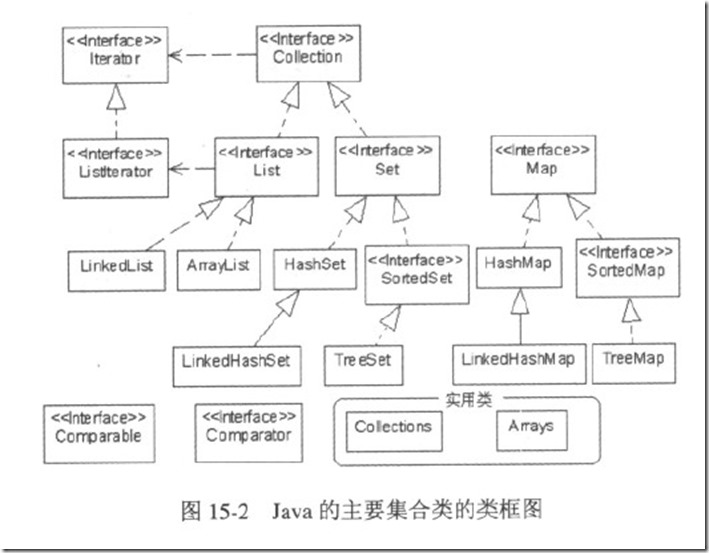
java集合总结_Java中集合总结
Java数组的长度是固定的,为了使程序能够方便地存储和操作数目不固定的一组数据,JDK类库提供了Java集合,这些集合类都位于java.util包中,但是与数组不同的是,集合中不能存放基本类型数据,而只能存放对象的引…

区块链基本解读
最近看着这个区块链,稍有新得,写下菜鸟自己的理解,希望大牛多多指点。 总体心得,如果互联网技术解决的是通讯问题的话,区块链技术解决的是信任问题。 下面举个日常例子:打赌 比如A和B赌石头是否为天然玉石&…

PDO防注入原理分析以及使用PDO的注意事项 (转)
我们都知道,只要合理正确使用PDO,可以基本上防止SQL注入的产生,本文主要回答以下两个问题: 为什么要使用PDO而不是mysql_connect? 为何PDO能防注入? 使用PDO防注入的时候应该特别注意什么? 一、为何要优先使用PDO? P…

LSGO软件技术团队招新 线下组队学习
团队招新 LSGO软件技术团队(Dreamtech算法组)成立于2010年09月,团队主要从事地理信息系统、管理信息系统、计算机视觉等领域的应用开发,团队同时具有培养学生的重要职能,毕业学生分布在IBM、百度、阿里、腾讯、京东、…

java spring 配置文件_[Java教程]Spring配置文件
[Java教程]Spring配置文件02016-03-19 00:00:08Spring配置文件是集成了Spring框架的项目的核心,引擎从哪里开始,中间都执行了哪些操作,小谈一下它的执行流程。容器先是加载web.接着是applicationContext.一种方法是加入ContextLoaderServlet这…

王子朝:一种高效且容错的方法用于协作车辆定位
王子朝是华北电力大学计算机系大四的学生,Dreamtech成员,参加了多期Dreamtech与Datawhale联合组织的组队学习活动,现保送西安电子科技大学深造。 这篇图文是他在线下组队学习时,为大家分享自己所看论文的总结。 希望参与我们组队…

python文件句柄_Python文件操作
classfile(object):def close(self): #real signature unknown; restored from __doc__关闭文件"""close() -> None or (perhaps) an integer. Close the file.Sets data attribute .closed to True. A closed file cannot be used forfurther I/O operation…

XML简单的增改删操作
XML文件的简单增改删,每一个都可以单独拿出来使用。 新创建XML文件,<?xmlversion"1.0"encoding"utf-8"?> <bookstore> <bookgenre"fantasy"ISBN"2-3631-4"> <title>Oberons Legacy&l…

javascript推荐书籍
WEB前端研发工程师,在国内算是一个朝阳职业,这个领域没有学校的正规教育,大多数人都是靠自己自学成才。本文主要介绍自己从事web开发以来(从大二至今)看过的书籍和自己的成长过程,目的是给想了解 JavaScript或者是刚接触JavaScrip…

【青少年编程竞赛交流】10月份微信图文索引
10月份微信图文索引 由于“组队学习”这个公众号的功能主要是组织Datawhale社群中的学习者们每个月的组队学习,所以,我另外新建了这个微信公众号“青少年编程竞赛交流”,在这个公众号上分享有关青少年编程方面的知识。如果大家需要就关注这个…

java 简单万年历_JAVA实现的简单万年历代码
本文实例讲述了JAVA实现的简单万年历。分享给大家供大家参考,具体如下:import java.util.Scanner;public class PrintCalendar {public static void main(String[] args) {int years 0;int month 0;int days 0;boolean isRun false;//從控制台輸入年…

mongoDB 入门指南、示例
http://www.cnblogs.com/hoojo/archive/2011/06/01/2066426.html mongoDB 入门指南、示例 上一篇:简单介绍mongoDB 一、准备工作 1、 下载mongoDB 下载地址:http://www.mongodb.org/downloads 选择合适你的版本 相关文档:http://www.mongodb.…
中国电子学会图形化四级编程题:成语接龙
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

sidecar学习
1、SideCar的出现 微服务的结构是细粒度的,由多个服务构成,支持不同的服务用不同的语言来编写,比如a服务用python,b服务用java,C服务用php等,我们称为异构语言,那么在利用zuul来代理访问服务的时…

java整数常量区_在Java中,我可以用二进制格式定义一个整数常量吗?
所以,随着Java SE 7的发布,二进制表示法是标准的。 如果你对二进制有一个很好的理解,语法是非常简单明了的。byte fourTimesThree 0b1100; byte data 0b0000110011; short number 0b111111111111111; int overflow 0b1010101010101010101…

[LeetCode 120] - 三角形(Triangle)
问题 给出一个三角形,找出从顶部至底部的最小路径和。每一步你只能移动到下一行的邻接数字。 例如,给出如下三角形: [ [2], [3,4], [6,5,7], [4,1,8,3] ] 从顶部至底部的最小路径和为11(即235111)。 注意: …
中国电子学会scratch等级考试四级编程题:找出出现次数最多的数字
「青少年编程竞赛交流群」已成立(适合6至18周岁的青少年),公众号后台回复【Scratch】或【Python】,即可进入。如果加入了之前的社群不需要重复加入。 我们将有关编程题目的教学视频已经发布到抖音号21252972100,小马老…

人工智能 有信息搜索 (启发式)
一、最佳优先搜索 根据评价函数选择表现的最佳的节点进行扩展 最佳优先搜索 best-first-search 算法 不同的方法有不同的评价函数 启发函数,标记h(x) h(n)从节点n到目标的最低耗散估计值 启发函数是额外信息的一种最普通的形式 二、贪婪最佳优先搜索 最先扩展离目标…

java 排序算法 讲解_java实现排序算法之冒泡排序法详细讲解
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序。这…

24、线程控制
线程有一套完整的与其有关的函数库可供调用,它们中的绝大多数函数名都以pthread_开头。为了调用这些函数库,必须在程序中包含头文件pthread.h,并且在比那一程序时使用选项-lpthread来链接线程库。 1、线程标识 就像每个进程有一个进程ID一样,…

Datawhale组队学习周报(第038周)
本周报总结了从 11月01日至11月07日,Datawhale组队学习的运行情况,我们一直秉承“与学习者一起成长的理念”,希望这个活动能够让更多的学习者受益。 第 30 期组队学习一共 8 门开源课程,共组建了 8 个学习群,参与的学…

OpenGL概念辨析: 窗口,视口,裁剪区域
1.窗口:这就不用解释了吧 2.视口:就是窗口中用来显示图形的一块矩形区域,它可以和窗口等大,也可以比窗口大或者小。只有绘制在视口区域中的图形才能被显示,如果图形有一部分超出了视口区域,那么那一部分是看…

java源码推荐_基于java的推荐系统实现源代码
【实例简介】常用推荐算法java实现~涉及多种相似度计算,比如cosine相似度,欧氏距离等~(recommand algirithm )【实例截图】【核心代码】RecommendSystemJavaCode└── Recommend└── src├── collaborative│ ├── cache│ │ ├── FileS…

ref与out的区别
前一段时间老用ref与out 感觉他们的效果差不多,就去网上查了一下他们的区别,网上说的概念性的东西太多了,后来通过自己的摸索发现他们有一个规律 ref: 在引用方法之外必须赋初值 static void TestRefAndRef(){string s1"test";Test…
【组队学习】【31期】组队学习内容详情
第31期 Datawhale 组队学习活动马上就要开始啦! 本次组队学习的内容为: IOS开发基于Python的办公自动化吃瓜教程——西瓜书南瓜书LeetCode 刷题李宏毅机器学习(含深度学习)动手学数据分析SQL编程语言数据可视化(Matpl…

区块链到底是什么?
2019独角兽企业重金招聘Python工程师标准>>> 欢迎大家前往腾讯云社区,获取更多腾讯海量技术实践干货哦~ 翻译人:ArrayZoneYour,该成员来自云社区翻译社 原文链接:https://www.investinblockchain.com/what-exactly-is-…

java怎么返回xml_java – 如何从Web服务返回XML
这可能是疯狂/愚蠢/愚蠢/冗长的问题之一,因为我是网络服务的新手.我想写一个Web服务,它将以XML格式返回答案(我正在使用我的服务进行YUI自动完成).我正在使用Eclipse和Axis2并遵循http://www.softwareagility.gr/index.php?qnode/21我希望以下列格式回复代码元素的数量可能因响…