hdu3321

Problem Description

Professor Brute is not good at algorithm design. Once he was asked to solve a path finding problem. He worked on it for several days and finally came up with the following algorithm:

Any fool but Brute knows that the function “funny” will be called too many times. Brute wants to investigate the number of times the function will be called, but he is too lazy to do it.
Now your task is to calculate how many times the function “funny” will be called, for the given a, b and n. Because the answer may be too large, you should output the answer module by P.

Input

There are multiple test cases. The first line of the input contains an integer T, meaning the number of the test cases.
For each test cases, there are four integers a, b, P and n in a single line.
You can assume that 1≤n≤1000000000, 1≤P≤1000000, 0≤a, b<1000000.

Output

For each test case, output the answer with case number in a single line.

Sample Input

3 3 4 10 3 4 5 13 5 3 2 19 100

Sample Output

Case #1: 2 Case #2: 11 Case #3: 12

由题意不难推出以下的递推公式: f[n]=f[n-1]*f[n-2],f[1]=a,f[2]=b;(当然，最后的结果不要忘记Mod p)

对于较小的N，直接一个循环求解即可。然而此题的N可达到10^9,显然在1秒的时限内，这种方法不再奏效。

仔细观察，发现每个f[n]都可以表示成a^t1*b^t2的形式,且不难推出对于某个N:

(1)N=1,则t1=1,t2=0; (2)N=2,则t1=0,t2=1;

(3) N>=3,t1=F(N-2),t2=F(N-1),其中F(n)表示第n个Fibonacci数

有了以上的信息，不难想到可以先运用矩阵连乘+快速幂 迅速求出F(N-1),F(N-2),再用运用快速幂算法处理(a^t1*b^t2) mod p，然而由于此处的N可以达到10^9,这样大的Fibonacci数F(N-1)已经远远超过了c++任何的内置类型，所以要想办法利用mod p这个条件

M1:利用数论中的Euler Phi函数，此处不作讨论

M2:由于p<=10^6,由鸽笼原理易知对于任意的正整数a, a^n mod p(n=0,1,2,3……)必然存在一个固定长度循环结（具体的求循环结的方法见代码）,在此处不妨假设：

a^n mod p从 n=starta 处开始，存在一个长度为rlena的循环结;

b^n mod p从 n=startb 处开始，存在一个长度为rlenb的循环结;

由此得到以下结论:

a^t1 mod p=a^t1 mod p, if t1<=starta+rlena

=a^(starta+(t1-starta) mod rlena)) mod p, if t1>starta+rlena  (*)

（b的相关表达式类似a)

所以对于两个相乘的矩阵(此处为2阶):

将(*)处得结论运用到 矩阵连乘+快速幂 求a的模p的等价系数t1’的过程中,即

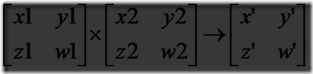
令x3=(x1*y1+x2*y2)则if x3<=starta + rlena, x’=x3; else x’=(starta+(x3-rlena) mod rlena) rlena,求y’,z’,w’的方法类似

按照上述的类似方法求出b的模p的等价系数t2’,最后再利用快速幂求出(a^t1’*b^t2’) mod p这个最终结果

以下是实现代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include <cstdlib>
using namespace std;
typedef long long bint;

#define size 1001000
bint que[size];
int app[size];

void find_repeat_len(int a,int p,int& rlen,int& start){
    bint mo=a%p; int index=1;
    que[index]=mo; app[mo]=index; mo=mo*a%p;
    while (!app[mo]){++index;
    que[index]=mo; app[mo]=index; mo=mo*a%p;
    }
    rlen=index-app[mo]+1; start=app[mo];
}
int ma[3][3],mb[3][3];
#define fun(x,st,rlen) ((x)<st+rlen?(x):st+((x)-st)%rlen)
void matrix_multi(int a[][3],int b[][3],int c[][3],int rlen,int st){
    bint x1,y1,z1,w1; bint x2,y2,z2,w2;
    x1=a[1][1]; y1=a[1][2]; z1=a[2][1]; w1=a[2][2];
    x2=b[1][1]; y2=b[1][2]; z2=b[2][1]; w2=b[2][2];
    bint tp;
    tp=x1*x2+y1*z2; c[1][1]=fun(tp,st,rlen);
    tp=x1*y2+y1*w2; c[1][2]=fun(tp,st,rlen);
    tp=z1*x2+w1*z2; c[2][1]=fun(tp,st,rlen);
    tp=z1*y2+w1*w2; c[2][2]=fun(tp,st,rlen);
}
int get_power(int rlen,int start,int kth){
    //求第kth个Fibnacci数，并利用循环节化简指数
    if (kth<=2) return 1;
    kth-=2;
    ma[1][1]=0; ma[1][2]=1; ma[2][1]=1; ma[2][2]=1;
    mb[1][1]=1; mb[1][2]=0; mb[2][1]=0; mb[2][2]=1;
    while (kth){
        if (kth&1) matrix_multi(mb,ma,mb,rlen,start);
        matrix_multi(ma,ma,ma,rlen,start); kth>>=1;
    }
    bint tp=mb[2][1]+mb[2][2];
    return fun(tp,start,rlen);
}


void solveit(int a,int b,int p,int n){
    if (n==1) printf("%d\n",a%p);
    else if (n==2) printf("%d\n",b%p);
    else {
        int rlena,rlenb,starta,startb;
        memset(app,0,sizeof(int)*(p+10));
        find_repeat_len(a,p,rlena,starta);
        int powa=get_power(rlena,starta,n-2);
        bint ans=que[powa];
        memset(app,0,sizeof(int)*(p+10));
        find_repeat_len(b,p,rlenb,startb);
        int powb=get_power(rlenb,startb,n-1);
        ans=ans*que[powb]%p;
        printf("%lld\n",ans);
    }
}
int main() {
    int testnum;
    scanf("%d",&testnum);
    int casenum=0;
    while (testnum--){++casenum; printf("Case #%d: ",casenum);
    int a,b,p,n;
    scanf("%d%d%d%d",&a,&b,&p,&n);
    solveit(a,b,p,n);
    }
    return 0;
}

Quote of the Day:
In life, as in chess, forethought wins.
--Charles Buxton