1.自底向上的分析
最普通的自底向上算法称作LR(1)分析( LR(1)parsing) ( L表示由左向右处理输入,R表示生成了最右推导,而数字1则表示使用了先行的一个符号)。
1.1自底向上分析概览
自底向上的分析程序使用了显式栈来完成分析,这与非递归的自顶向下的分析程序相类似。分析栈包括记号和非终结符,以及一些后面将讨论到的其他信息。自底向上的分析开始时栈是空的,在成功分析的末尾还包括了开始符号。
自底向上的分析示意为:
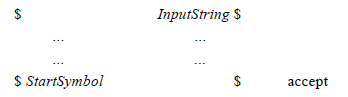
分析栈在左边,输入位于正中间,而分析程序的动作则在右边。
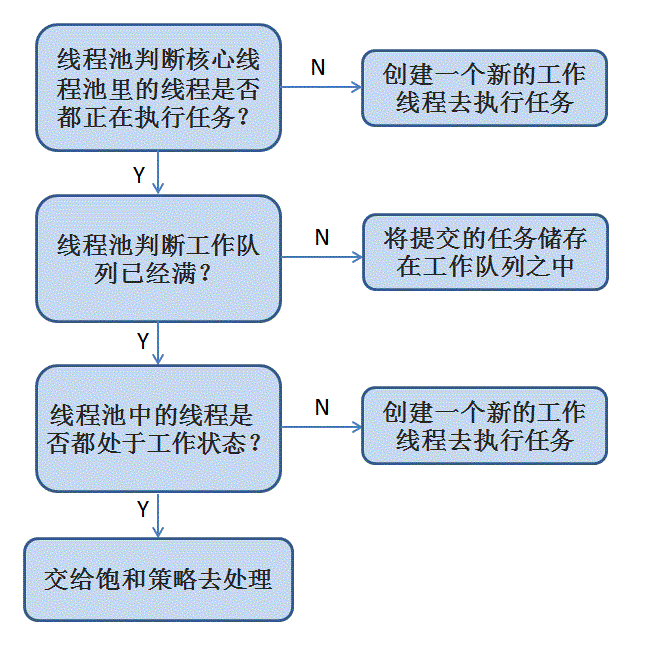
自底向上的分析程序有两种可能的动作(除“接受”之外):
1) 将终结符从输入的开头移进到栈的顶部。
2) 假设有BNF选择A→α,将栈顶部的串α归约为非终结符A。
因此自底向上的分析程序有时称作是移进-归约分析程序。
移进动作是由书写单词s h i f t指出的。归约动作则由书写re d u c e单词给出且指出在归约中所用的B N F选择。
另一个特征是(由于技术原因???):
总是将文法与一个新的开始符号一同扩充 这就意味着若S是开始符号,那么就将新的开始符号S’增加到文法中,同时还添加一个单元产生式到前面的开始符号中:
S’ → S
例:
E’→ E
E → E + n | n

移进-归约分析程序描绘出输入串的最右推导,但推导步骤的顺序却是颠倒的。
在表5 - 2中,相对应的推导是E’ => E => E + n => n + n
这样的推导中的终结符和非终结符的每个中间串都称作右句型。
句柄:(参考:https://blog.csdn.net/it_dream_er/article/details/53612006)
直接短语中的最左直接短语为该句型的句柄。
移进-归约分析程序将终结符从输入移进到栈直到它能执行一个归约以得到下一个右句子格式。它发生在位于栈顶部的符号串匹配用于下一个归约的产生式的右边。这个串、它在右句子格式中发生的位置以及用来归约它的产生式被称作右句型的句柄(handle) 。
例如,在右句子格式n + n 中,它的句柄是由最左边的单个记号n 与用来归约它以产生新的右句型E + n的产生式E→n 组成的串。这个新句型的句柄是整个串E + n (一个可行的前缀)以及产生式E→E + n。有时由于表示法上的弊端,我们要用串本身来作为句柄。
判断分析中的下一个句柄是移进-归约分析程序的主要任务。
1.2 LR(0)项的有穷自动机与LR(0)分析
1.2.1 LR(0)项
例:
S’→S
S→( S ) S | ε
这个文法存在着3个产生式选择和8个项目:
S’→.S
S’→S.
S→. ( S ) S
S→( .S ) S
S→( S. )S
S→( S ) .S
S→( S )S.
定义:
上下文无关文法的LR (0)项(LR(0) item)(或简写为项( item ) )是在其右边带有区分位置的产生式选择。我们可用一个句点(当然它就变成了元符号,而不会与真正的记号相混淆)来指出这个区分的位置。所以若A→α是产生式选择,且若β和γ 是符号的任何两个串(包括空串),且存在着βγ = α,那么A→β.γ 就是LR(0)项。之所以称作LR(0)项是由于它们不包括先行的显式引用。
项目概念的思想就是指项目记录了特定文法规则右边识别中的中间步骤。特别地,项目A→β.γ是由文法规则选择A→α构成(其中 α = βγ ),这一点意味着早已看到了β,且可能从下一个输入记号中获取γ。从分析栈的观点来看,这就意味着β必须出现在栈的顶部。项目A→.α 意味着将要利用文法规则选择 A→α 识别A(将这样的项目称作初始项(initial item)。项目 A→α. 意味着α现在位于分析栈的顶部,而且若 A→α 在下一个归约中使用的话,它有可能就是句柄(将这样的项目称作完整项(complete item))。
1.2.2 项目的有穷自动机
注:概念解释:闭包:
参考:https://blog.csdn.net/n6323438/article/details/51996551
https://blog.csdn.net/woailuo453786790/article/details/51254124
LR (0)项可作为一个保持有关分析栈和移进-归约分析过程的信息的有穷自动机的状态来使用。
对1.2.1的例子:
NFA:
文法有8个LR(0)项,所以这个NFA就有8个状态。
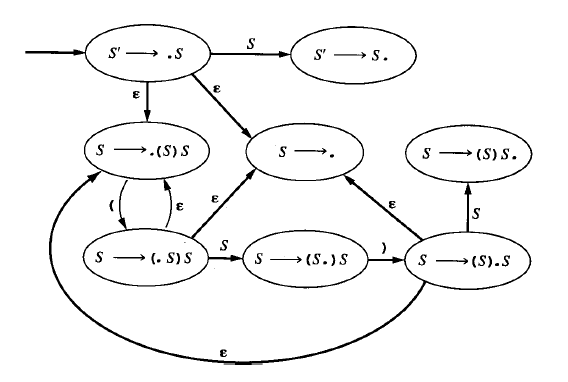
DFA:
DFA的开始状态是由项目S’→ .S 组成的集合的 ε- 闭包,即集合{S’→.S, S’→. ( S ) S, S’ →.}。由于S有一个从S’→ .S到S’→ S.的转换,所以也就存在着一个从开始状态到DFA状态{ S’→ S. } 的对应转换(不存在从S’→ S.到任何其他项目的转换)。在(上也有一个从开始状态到DFA状态的转换{ S→ (. S ) S, S→.( S ) S, S→. }({ S→ (.S ) S }的ε闭包。DFA状态{ S→ (. S ) S, S→ . ( S ) S, S→ . }在(上有到其自身的转换,在S上也有到{ S→ ( S.) S }的转换。这个状态在(上有到状态{ S→ ( S ). S,S→ .( S ) S, S → . }的转换。最后,这一最终状态在(上有到前面所构造的状态{ S→ (. S ) S, S→ .( S ) S, S → . }的转换。图是完整的D FA,为了便于引用还给各个状态编了号(按照惯例,状态0是开始状态)。
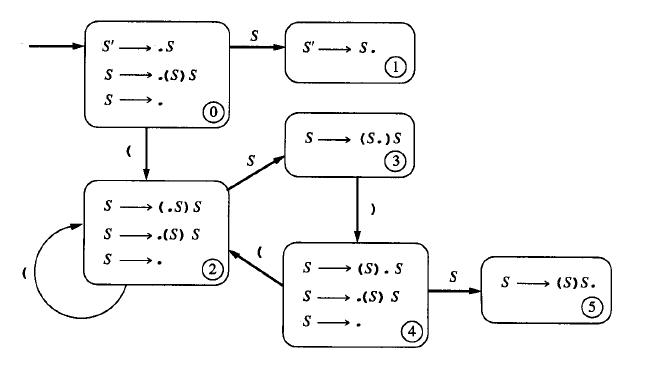
1.2.3 LR(0)分析算法
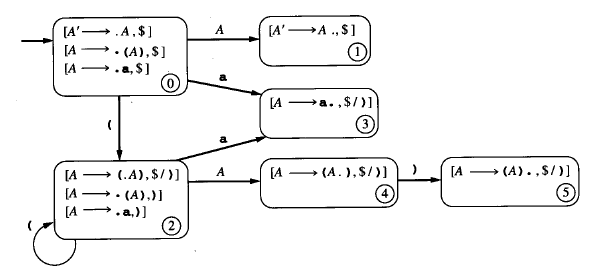
例:文法 A → (A)| a
LR(0)项:
状态0:初始状态
A’ → .A
A → .(A)
A → .a
状态1:(识别状态0 的第一个LR(0)项,接收A)
A’ → A.
状态2:(识别状态0的第三个项,接收a,较为简单)
A → a.
状态3:接收" ( " (接收a,将转到状态2)
A → (.A)
A → .(A)
A → .a
状态4:从状态3接收A
A → (A.)
状态5:从状态4接收 )
A → (A).
构造DFA:

以((a))分析动作:将状态数和字符都压入栈中:
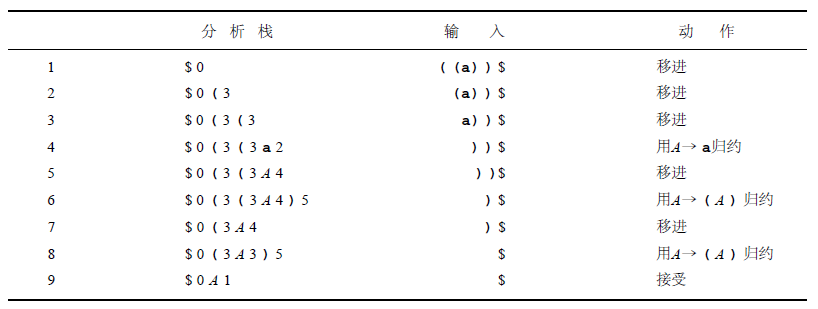
初步解释,待验证:
初始状态0
终止状态1
遇到状态2和状态5进行规约,状态1也是规约状态
分析表:
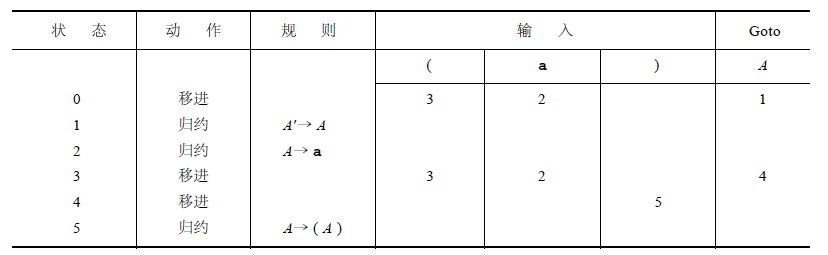
注:空白项表示的是识别出错。
1.3 SLR(1)分析
名词解释:https://blog.csdn.net/zuzhiang/article/details/79047743
1.3.1 SLR(1)分析算法
通过使用输入串中下一个记号来指导它的动作。首先,它在一个移进之前先考虑输入记号以确保存在着一个恰当的DFA。其次,使用非终结符的Follow集合来决定是否应执行一个规约。
定义:SLR(1)分析算法(SLR(1) parsing algorithm)。令s 为当前状态(位于分析栈的顶部)。则动作可定义如下:
1. 若状态s 包含了格式A→α.Xβ的任意项目,其中X是一个终结符,且X是输入串
中的下一个记号,则动作将当前的输入记号移进到栈中,且被压入到栈中的新
状态是包含了项目A→aX.b的状态。
2. 若状态s 包含了完整项目A→γ.,则输入串中的下一个记号是在Follow(A)中,所
以动作是用规则A→γ 归约。用规则S’→S归约与接受等价,其中S是开始状态;
只有当下一个输入记号是$时,这才会发生。在所有的其他情况中,新状态都
是如下计算的:删除串α和所有它的来自分析栈中的对应状态。相对应地,
DFA回到α开始构造的状态。通过构造,这个状态必须包括格式B→γ. Aβ的一
个项目。将A压入到栈中,并将包含了项目B→αA.β的状态压入。
3. 若下一个输入记号都不是上面两种情况所提到的,则声明一个错误。
SLR(1)文法判断:
当且仅当对于任何状态s,满足一下两个条件
1) 对于在s 中的任何项目A→α.Xβ,当X是一个终结符,且X在Follow (B) 中时,s 中没有完整的项目B→γ.。
2) 对于在s 中的任何两个完整项目A→α.和B→β.,Follow (A)∩ Follow(B)为空。
若第1个条件不满足,就表示这是一个移进-归约冲突(shift-reduce conflict)。
若第2个条件不满足,就表示这是一个归约-归约冲突(reduce-reduce conflict)。
例:
接着1.2.2的例子进行,分析串()()
SLR(1)分析表:

分析动作

1.3.2 用于分析冲突的消除二义性规则
在移进-归约冲突中,总是选取移进而不是归约 ,解决移进-归约冲突。
但是归约-归约冲突就要复杂一些了:这样的冲突通常(但并不是总是)指出文法设计中的一个错误(后面将给出这样冲突的示例)。
//待补充吧
1.3.3 SLR(1)分析能力的局限性
例:文法:
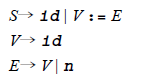
这个状态在 id 上有一个状态:
S → id.
V → id.
的转换。现在有 Follow (S) = {$}和 Follow (V) = { : =, $ }(由于有规则V→V := E所以有 :=,又由于E可以是V,所以有$ )。因此,SLR(1)分析算法要求在这个状态中有一个在输入符号$下的利用规则S→ id 和规则V→ id 实现的归约(这是一个归约-归约冲突)。这个分析冲突实际上是一个由SLR(1)方法的缺点所引起的“假冒”问题。实际上当输入为$时,用V → id 实现的归约永远也不应该在这个状态中,这是由于只有到看到记号:=和被移进后,变量才会出现在语句的末端。
1.3.4 SLR(k)文法 ps:先记着吧,不看了
同其他分析算法一样, SLR(1)分析算法可被扩展为 SLR(k)分析,其中的分析动作是基于k≥1个先行的符号之上。利用上一章定义的集合Firstk和
Followk,Slr(k)分析程序使用以下两个规则:
1) 若状态s 包含了格式A→α.Xβ(X是一个记号),且Xw∈ Firstk(Xβ)是输入串中之后的k个记号,那么该动作就是将当前输入记号移进到栈中,而且被压入到栈中的新状态是包含了项目A→α.Xβ的状态。
2) 若状态s 包含了完整项目A→α.,且w ∈ Followk(A)是输入串中之后的k 个记号,则动作用规则A→α归约。
当k > 1时,SLR(k)分析比SLR(1)分析更强大,但由于分析表的大小将按k的指数倍增长,所以它又要复杂许多。非SLR(1)的典型语言构造可利用LRLA(1)分析程序处理得更好一些,它可使用标准的消除二义性的规则,或将文法重写。
1.4 一般的LR(1)和LALR(1)分析
L R ( 1 )规范( canonical)分析。这种方法解决了上一节最后所提到的SLR(1)分析中出现的问题,但它却复杂得多。实际上在绝大多数情况下,通常地,一般的LR(1)分析太复杂以至于不能在大多数情况下的分析程序的构造中使用。幸运的是,一般的LR(1)分析的一个修正——称作LALR(1) (即“先行” LR分析)在保留了LR (1)分析的大多数优点之外还保留了SLR(1)方法的有效性。LALR(1)方法已成为诸如用于诸如 Yacc 这样的分析程序生成器所选用的方法。
1.4.1 LR(1)项的有穷自动机
LR(1)项应是由LR(0)项和一个先行记号组成的对。利用中括号将LR(1)项写作
[A→α.β α ]
其中A→α.β是一个LR(0)项,而α 则是一个记号(先行)。
LR(1)分析的自动机的非 ε- 转换:
定义: LR(1)转换(第1部分)的定义(definition of LR(1) transitions (part 1))。假设有LR(1)项目[A→α.Xγ, a],其中X是任意符号(终结符或非终结符),那么X就有一个到项目[A→αX.γ, a]的转换。
请注意在这种情形下,两个项目中都出现了相同的先行a,所以这些转换并不会引起新的先行的出现。只有 ε- 转换才“创建”新的先行,如下所示。
定义: LR(1)转换(第2部分)的定义(definition of LR(1) transitions (part 2))。假设有LR(1)项目[A→α.Bγ,a],其中B是一个非终结符,那么对于每个产生式B→β和在 First(γa) 中的每个记号β都有到项目[B→.β,b] 的 ε- 转换。
例:
文法: A→ ( A ) | a
通过扩充文法以及构造初始的LR(1)项目[A’→.A, $]来构建它的LR(1)项目集合的DFA。
状态0: [A’→.A, $]
[A→. ( A ), $]
[A→. a, $]
状态1: [A’→A., $]
状态2: [A→ ( .A ), $ ]
[A→. ( A ), ) ]
[A→. a, ) ]
状态3: [A→a ., $ ]
状态4: [A→ ( A. ), $]
状态5: [A→ ( . A ), ) ]
[A→ . ( A ), ) ]
[A→. a, ) ]
状态6: [A→a ., ) ]
状态7: [A→ ( A ) ., $]
状态8: [A→ ( A . ), ) ]
状态9: [A→ ( A ) ., ) ]
DFA:

1.4.2 LR(1)分析算法
一般的LR(1)分析算法令s 为当前状态(位于分析栈的顶部),则动作定义如下:
① 若状态s 包含了格式[A→a.Xb, a]的任意LR(1)项目,其中X是一个终结符且是输入串中
的下一个记号,则动作就是将输入记号移进到栈中,且被压入到栈中的新状态是包含了LR(1)
项目[A→aX.b, a]的状态。
② 若状态s 包含了完整的LR(1)项目[A→a., a],且输入串中的下一个记号是a,则动作就是
用规则A→a归约。用规则S’→S (其中S是开始状态)实现的归约等价于接受(只有当下一个输入
记号是$时才发生)。在其他情况下,新状态的计算如下:将串a以及与它对应的所有状态从分
析栈中删去。相应地DFA返回到a开始构造的状态。通过构造,这个状态必须包括格式[B→
a.Ab, b]的L R ( 1 )项目。将A压入到栈中,并压入包含了项目[B→aA.b, b] 的状态。
③ 若下一个输入记号不是上面所述的任何一种情况,则声明一个错误。
LR(1)文法判断:
① 对于在s 中的任何项目[A→a.Xb, a],且X是一个终结符,则在s 中没有格式[B→b., X ]的项目(否则就有一个移进-归约冲突)。
② 在s 中没有格式[A→a., a]和[B→b., a]的两个项目(否则就有一个归约-归约冲突)。
可从表达一般L R ( 1 )分析算法的L R ( 1 )项目集合的D FA中构造出一个分析表。该表具有与S L R ( 1 )分析程序的表格完全相同的格式,如下例所示。
例: 接1.4.2的例子
在归约动作中的文法规则选择使用了以下的编号:
(1) A→(A)
(2) A→a
因此在状态3中带有先行$的项r 2指出了规则A→a 实现的归约。
一般LR(1)分析表
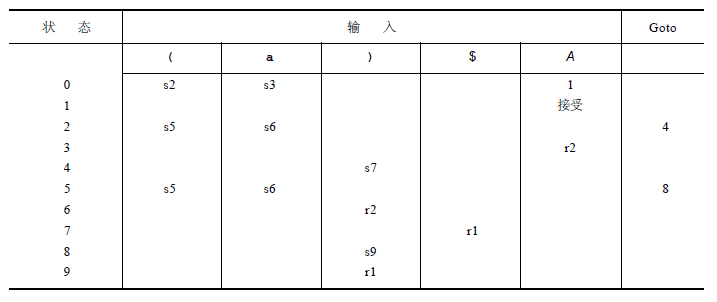
例:解决SLR(1)文法的先行问题
文法:
S→ i d | V : = E
V→ i d
E→ V | n
为这个文法构造LR(1)项目集合的D FA。其开始状态是项目[S’→.S, $]的闭包。
状态0:
[S’→.S, $]
[S →.i d, $]
[S →.V : = E, $]
[V →.i d, : =]
状态1:
[S’→.S, $]
状态2:
[S→.i d, $]
[V →.i d, . = ]
状态3:
[S →V . : = E, $]
状态4:
[S →V : = .E, $]
[E →.V, $]
[E →.n, $]
[V →.i d, $]
。。。
LR(1)项目集合的DFA
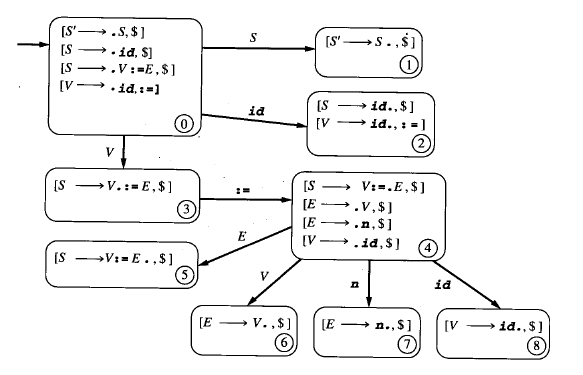
状态2,这是SLR(1)分析引起的冲突状态。LR(1)项目可由它的先行清晰地区分出两个规约。
1.4.3 LALR(1)分析
LALR(1)分析算法表明了它使得标识所有这样的状态和组合它们的先行有意义。在这样做时,我们总是必须以一个与LR(0)项目中的DFA相同的DFA作为结尾,但是每个状态都是以带有先行集合的项目组成。在完整项目的情况下,这些先行集合通常比相应的Follow集合小;因此,LRLA(1)分析保留了LR(1)分析优于SLR(1)分析的一些特征,但是仍具有在LR(0)项目中的DFA尺寸较小的特点。
LALR(1)分析的原则:
(1) LALR(1)分析的第1个原则
L R ( 1 )项目的D FA的状态核心是L R ( 0 )项目的D FA的一个状态。
(2) LALR(1)分析的第2个原则
若有具有相同核心的LR(1)项目的DFA的两个状态s1 和s2,假设在符号X上有一个从s1 到状
态t1 的转换,那么在X上就还有一个从状态s2 到一个状态t2 的转换,且状态t1 和t2 具有相同的
核心。
例:续上面的例子