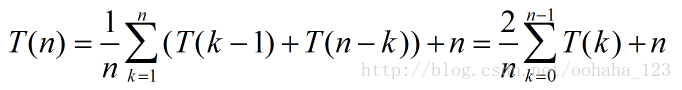原理:
通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
#include <stdio.h> #define MAXSIZE 9typedef struct {int r[MAXSIZE+1]; //r[0] 作为哨兵int length; //待排序的数组长度 }SqList;void print(SqList L){int i;for(i=1; i<MAXSIZE; i++){printf("%3d,",L.r[i]);}printf("%3d\n",L.r[i]); }void swap(SqList * L, int i, int j){int temp=L->r[i];L->r[i]=L->r[j];L->r[j]=temp; }void QuickSort(SqList * L){void Qsort(SqList * L, int low, int high);Qsort(L,1,L->length); }void Qsort(SqList * L, int low, int high){int Partition(SqList * L,int low, int high);int pivot;//注意在边界的地方要判断,pivot=1或者pivot=length,做处理if(low < high){pivot=Partition(L, low, high);//将L->[low-high]一分为二,返回pivotkey所在位置的下标Qsort(L,low,pivot-1);Qsort(L,pivot+1,high);} }int Partition(SqList * L,int low, int high){int pivotkey=L->r[low];while(low < high){while(low < high && L->r[high]>=pivotkey) high--;swap(L,low,high);while(low < high && L->r[low]<=pivotkey) low++;swap(L,low,high);}return low; //返回pivotkey当前的下标 }int main(){SqList L;int num[MAXSIZE+1]={9,7,4,3,2,1,6,5,9,8};for(int i=0; i<10; i++){L.r[i] = num[i];}L.length=9; //快排QuickSort(&L);print(L); return 0; }
时间复杂度
最优情况下时间复杂度
= 2^2 T[ n/ (2^2) ] + 2n
= 2^2 { 2 T[n/ (2^3) ] + n/(2^2)} + 2n ----------------第三次递归
= 2^3 T[ n/ (2^3) ] + 3n
= 2^m T[1] + mn ----------------第m次递归(m次后结束),只需要对1个元素的情况进行复杂符分析,即T(1)。
当最后平分的不能再平分时,也就是说把公式一直往下跌倒,到最后得到T[1]时,说明这个公式已经迭代完了(T[1]是常量了)。
得到:T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn;
T[n] = 2^m T[1] + mn ;其中m = logn;
T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ;其中n为元素个数
又因为当n >= 2时:nlogn >= n (也就是logn > 1),所以取后面的 nlogn,即最有情况下的时间复杂度为O(nlogn);(注意:这里logn表示以2为底的n的对数)
最差情况下时间复杂度 这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n;
平均时间复杂度