JavaScript词法作用域的简单介绍
by Michael McMillan
迈克尔·麦克米兰(Michael McMillan)
JavaScript词法作用域的简单介绍 (An easy intro to Lexical Scoping in JavaScript)
Lexical scoping is a topic that frightens many programmers. One of the best explanations of lexical scoping can be found in Kyle Simpson’s book You Don’t Know JS: Scope and Closures. However, even his explanation is lacking because he doesn’t use a real example.
词法作用域是一个使许多程序员感到恐惧的话题。 词法作用域的最佳解释之一可以在Kyle Simpson的《 You't Know JS:范围和闭包》一书中找到。 但是,甚至没有他的解释,因为他没有使用真实的例子。
One of the best real examples of how lexical scoping works, and why it is important, can be found in the famous textbook, “The Structure and Interpretation of Computer Programs” (SICP) by Harold Abelson and Gerald Jay Sussman. Here is a link to a PDF version of the book: SICP.
关于词法作用域如何工作以及为什么它很重要的最好的真实例子之一,可以在Harold Abelson和Gerald Jay Sussman着名的教科书《计算机程序的结构和解释》(SICP)中找到。 这是该书的PDF版本的链接: SICP 。
SICP uses Scheme, a dialect of Lisp, and is considered one of the best introductory computer science texts ever written. In this article, I’d like to revisit their example of lexical scoping using JavaScript as the programming language.
SICP使用Scheme,这是Lisp的方言,被认为是有史以来最好的入门计算机科学课本之一。 在本文中,我想回顾他们使用JavaScript作为编程语言的词法作用域示例。
我们的例子 (Our example)
The example Abelson and Sussman used is computing square roots using Newton’s method. Newton’s method works by determining successive approximations for the square root of a number until the approximation comes within a tolerance limit for being acceptable. Let’s work through an example, as Abelson and Sussman do in SICP.
Abelson和Sussman使用的示例是使用牛顿方法计算平方根。 牛顿法的工作原理是确定一个数字的平方根的逐次逼近,直到逼近在可接受的公差范围内。 让我们来看一个例子,就像Abelson和Sussman在SICP中所做的那样。
The example they use is finding the square root of 2. You start by making a guess at the square root of 2, say 1. You improve this guess by dividing the original number by the guess and then averaging that quotient and the current guess to come up with the next guess. You stop when you reach an acceptable level of approximation. Abelson and Sussman use the value 0.001. Here is a run-through of the first few steps in the calculation:
他们使用的示例找到2的平方根。首先对2的平方根进行猜测,即1。通过将原始数字除以猜测值,然后对该商和当前猜测值求平均值,可以改善此猜测值。提出下一个猜测。 当您达到可接受的近似水平时,您将停止。 Abelson和Sussman使用值0.001。 这是计算的前几个步骤的贯穿过程:
Square root to find: 2First guess: 1Quotient: 2 / 1 = 2Average: (2+1) / 2 = 1.5Next guess: 1.5Quotient: 1.5 / 2 = 1.3333Average: (1.3333 + 1.5) / 2 = 1.4167Next guess: 1.4167Quotient: 1.4167 / 2 = 1.4118Average: (1.4167 + 1.4118) / 2 = 1.4142And so on until the guess comes within our approximation limit, which for this algorithm is 0.001.
依此类推,直到猜测在我们的近似极限之内,该近似极限为0.001。
牛顿方法JavaScript函数 (A JavaScript Function for Newton’s Method)
After this demonstration of the method the authors describe a general procedure for solving this problem in Scheme. Rather than show you the Scheme code, I’ll write it out in JavaScript:
在对该方法进行了演示之后,作者在Scheme中描述了解决此问题的一般过程。 我没有用Scheme代码显示,而是用JavaScript编写出来:
function sqrt_iter(guess, x) { if (isGoodEnough(guess, x)) { return guess; } else { return sqrt_iter(improve(guess, x), x); }}Next, we need to flesh out several other functions, including isGoodEnough() and improve(), along with some other helper functions. We’ll start with improve(). Here is the definition:
接下来,我们需要充实其他几个函数,包括isGoodEnough()和Improvement()以及其他一些辅助函数。 我们将以改良()开始。 这是定义:
function improve(guess, x) { return average(guess, (x / guess));}This function uses a helper function average(). Here is that definition:
此函数使用辅助函数average()。 这是定义:
function average(x, y) { return (x+y) / 2;}Now we’re ready to define the isGoodEnough() function. This function serves to determine when our guess is close enough to our approximation tolerance (0.001). Here is the definition of isGoodEnough():
现在我们准备定义isGoodEnough()函数。 此函数用于确定我们的猜测何时足够接近我们的近似公差(0.001)。 这是isGoodEnough()的定义:
function isGoodEnough(guess, x) { return (Math.abs(square(guess) - x)) < 0.001;}This function uses a square() function, which is easy to define:
此函数使用square()函数,该函数易于定义:
function square(x) { return x * x;}Now all we need is a function to get things started:
现在,我们需要的是一个可以开始的功能:
function sqrt(x) { return sqrt_iter(1.0, x);}This function uses 1.0 as a starting guess, which is usually just fine.
此函数使用1.0作为开始猜测,通常很好。
Now we’re ready to test our functions to see if they work. We load them into a JS shell and then compute a few square roots:
现在,我们准备测试我们的功能,看看它们是否有效。 我们将它们加载到JS shell中,然后计算一些平方根:
> .load sqrt_iter.js> sqrt(3)1.7321428571428572> sqrt(9)3.00009155413138> sqrt(94 + 87)13.453624188555612> sqrt(144)12.000000012408687The functions seem to be working well. However, there is a better idea lurking here. These functions are all written independently, even though they are meant to work in conjunction with each other. We probably aren’t going to use the isGoodEnough() function with any other set of functions, or on its own. Also, the only function that matters to the user is the sqrt() function, since that’s the one that gets called to find a square root.
这些功能似乎运行良好。 但是,这里有一个更好的主意。 这些功能都是独立编写的,即使它们旨在相互配合工作也是如此。 我们可能不会将isGoodEnough()函数与任何其他函数集一起使用,或者单独使用。 另外,对用户而言唯一重要的函数是sqrt()函数,因为该函数被调用来查找平方根。
块作用域隐藏助手功能 (Block Scoping Hides Helper Functions)
The solution here is to use block scoping to define all the necessary helper functions within the block of the sqrt() function. We are going to remove square() and average() from the definition, as those functions might be useful in other function definitions and aren’t as limited to use in an algorithm that implements Newton’s Method. Here is the definition of the sqrt() function now with the other helper functions defined within the scope of sqrt():
此处的解决方案是使用块作用域来在sqrt()函数的块内定义所有必需的辅助函数。 我们将从定义中删除square()和average(),因为这些函数在其他函数定义中可能很有用,并且不限于在实现牛顿方法的算法中使用。 这是sqrt()函数的定义,以及在sqrt()范围内定义的其他辅助函数:
function sqrt(x) { function improve(guess, x) { return average(guess, (x / guess)); } function isGoodEnough(guess, x) { return (Math.abs(square(guess) - x)) > 0.001; } function sqrt_iter(guess, x) { if (isGoodEnough(guess, x)) { return guess; } else { return sqrt_iter(improve(guess, x), x); } } return sqrt_iter(1.0, x);}We can now load this program into our shell and compute some square roots:
现在我们可以将该程序加载到我们的shell中并计算一些平方根:
> .load sqrt_iter.js> sqrt(9)3.00009155413138> sqrt(2)1.4142156862745097> sqrt(3.14159)1.772581833543688> sqrt(144)12.000000012408687Notice that you cannot call any of the helper functions from outside the sqrt() function:
请注意,您不能从sqrt()函数外部调用任何辅助函数:
> sqrt(9)3.00009155413138> sqrt(2)1.4142156862745097> improve(1,2)ReferenceError: improve is not defined> isGoodEnough(1.414, 2)ReferenceError: isGoodEnough is not definedSince the definitions of these functions (improve() and isGoodEnough()) have been moved inside the scope of sqrt(), they cannot be accessed at a higher level. Of course, you can move any of the helper function definitions outside of the sqrt() function to have access to them globally as we did with average() and square().
由于这些函数的定义(improve()和isGoodEnough())已移至sqrt()范围内,因此无法在更高级别访问它们。 当然,您可以将任何辅助函数定义移到sqrt()函数之外,以像对average()和square()那样全局访问它们。
We have greatly improved our implementation of Newton’s Method but there’s still one more thing we can do to improve our sqrt() function by simplifying it even more by taking advantage of lexical scope.
我们极大地改进了牛顿方法的实现,但是还有更多事情可以做,以通过利用词汇范围进一步简化sqrt()函数来改进我们的sqrt()函数。
用词法范围提高清晰度 (Improving Clarity with Lexical Scope)
The concept behind lexical scope is that when a variable is bound to an environment, other procedures (functions) that are defined in that environment have access to that variable’s value. This means that in the sqrt() function, the parameter x is bound to that function, meaning that any other function defined within the body of sqrt() can access x.
词法作用域背后的概念是,当变量绑定到环境时,在该环境中定义的其他过程(函数)可以访问该变量的值。 这意味着在sqrt()函数中,参数x绑定到该函数,这意味着sqrt()主体内定义的任何其他函数都可以访问x。
Knowing this, we can simplify the definition of sqrt() even more by removing all references to x in function definitions since x is now a free variable and accessible by all of them. Here is our new definition of sqrt():
知道了这一点,我们可以通过删除函数定义中对x的所有引用来进一步简化sqrt()的定义,因为x现在是一个自由变量,并且所有变量都可以访问。 这是我们对sqrt()的新定义:
function sqrt(x) { function isGoodEnough(guess) { return (Math.abs(square(guess) - x)) > 0.001; } function improve(guess) { return average(guess, (x / guess)); } function sqrt_iter(guess) { if (isGoodEnough(guess)) { return guess; } else { return sqrt_iter(improve(guess)); } } return sqrt_iter(1.0);}The only references to parameter x are in computations where x’s value is needed. Let’s load this new definition into the shell and test it:
对参数x的唯一引用是在需要x值的计算中。 让我们将这个新定义加载到外壳中并对其进行测试:
> .load sqrt_iter.js> sqrt(9)3.00009155413138> sqrt(2)1.4142156862745097> sqrt(123+37)12.649110680047308> sqrt(144)12.000000012408687Lexical scoping and block structure are important features of JavaScript and allow us to construct programs that are easier to understand and manage. This is especially important when we begin to construct larger, more complex programs.
词法作用域和块结构是JavaScript的重要功能,使我们能够构建更易于理解和管理的程序。 当我们开始构建更大,更复杂的程序时,这一点尤其重要。
翻译自: https://www.freecodecamp.org/news/lexical-scoping-in-javascript-e876cd221b74/
相关文章:
Flex 布局详解 - 转自阮一峰老师
Flex 是 Flexible Box 的缩写,意为"弹性布局",用来为盒状模型提供最大的灵活性。任何的盒子都可以使用它。 下面我们来看一下使用 Flex 布局的容器的属性 flex-direction flex-wrap flex-flow justify-content align-items align-content 1.…

bzoj 1086: [SCOI2005]王室联邦
Description “余”人国的国王想重新编制他的国家。他想把他的国家划分成若干个省,每个省都由他们王室联邦的一个成员来管理。他的国家有n个城市,编号为1..n。一些城市之间有道路相连,任意两个不同的城市之间有且仅有一条直接或间接的道路。为…
在7分钟内深刻理解咖喱
Eric Elliott’s exceptional Composing Software series is initially what got me excited about functional programming. Its a must-read. 埃里克埃利奥特(Eric Elliott)杰出的合成软件系列最初使我对函数式编程感到兴奋。 这是必读的。 At one point in the series, he …

github后端开发面试题大集合(一)
作者:小海胆链接:https://www.nowcoder.com/discuss/3614?type0&order0&pos5&page0?fromwb来源:牛客网 转载自github,中文--->链接在这,英文---->链接在这文章较长,我把它拆分了三个部…
微信小程序左滑删除效果的实现完整源码附效果图
效果图: 功能描述,小程序列表左滑删除功能的实现完整源代码实现: <view wx:for{{friends}} wx:key"" wx:if{{groupType4}} catchtap"nav_oneChat" id"{{item._id}}" class"item p_r" style"…

Eclipse下修改工程名
一。 右键工程:Refactor->Rename,或选中工程按F2,修改名称 二。右键工程:Properties->Web Project Settings,修改Context Root三。1.找到项目所在位置(如图): 2.修改项目目录/.setting目录…

git操作手册_基本的Git手册
git操作手册介绍 (Introduction) Hi! I am Sanjula, and in this guide I hope to teach you a little bit about Git including:嗨! 我是Sanjula ,在本指南中,我希望教您一些有关Git的知识,包括: What Git is 什么是…

PHP 接入(第三方登录)QQ 登录 OAuth2.0 过程中遇到的坑
前言 绝大多数网站都集成了第三方登录,降低了注册门槛,增强了用户体验。最近看了看 QQ 互联上 QQ 登录的接口文档。接入 QQ 登录的一般流程是这样的:先申请开发者 -> 然后创建应用(拿到一组 AppId 和 AppKey)-> …
npm全局环境变量配置,全局配置cnpm
今天新电脑想安装node.js , 发现最新版本的node.js已经不支持win7了,但是又不想换系统,所以找了个旧版本,这里不多说了。如果找不到旧版本的node下载,可以去我的QQ交流群文件里面下载,QQ群号:17…

NTFS for Mac OS X:使用Brew安裝NTFS-3G
在最新的OSX系統中,其實已經完整兼容NTFS文件系統,只是出於安全考慮默認是以只讀模式掛載NTFS分區的,可以透過diskutil查詢硬碟UUID,重新以讀寫(rw)權限掛載,具體的可以參照這裡 當然,也有現成的軟體幫助你…

javascript开关_JavaScript开关案例简介
javascript开关In this short article, I will introduce you to JavaScript switch cases and how to use them with practical examples.在这篇简短的文章中,我将向您介绍JavaScript切换案例以及如何通过实际示例使用它们。 This article will explain better wi…

C++中一个class类对象占用多少内字节(7个例子,很清楚)
一个空的class在内存中多少字节?如果加入一个成员函数后是多大?这个成员函数存储在内存中什么部分? 一个Class对象需要占用多大的内存空间。最权威的结论是: *非静态成员变量总合。 *加上编译器为了CPU计算,作出的数据…

Java学习----到底调用哪一个方法(多态)
public class Father {public void print() {System.out.println("Father:print()");} } public class Son extends Father{// 方法的覆盖:子类重写父类的同名方法 Overridepublic void print() {System.out.println("Son:print()");}// Father…
mpvue 转uni-app 操作记录
1.创建一个uni-app 的项目,把原有的mpvue项目手动迁移过来 2.用到mpvue特性的代码,需要修改成uni-app 兼容的,例如 mpvue-wxparse 可以修改成 3.src/app.json 改成 pages.json ,路径格式需要改,如下格式 {"pages": [&…

桌面应用程序 azure_Azure Logic应用程序用例–黑色星期五
桌面应用程序 azureThis blog gives an overview of how Azure Serverless technologies came to rescue when the custom-built integration system went down. Also, it shows the high-level architecture solution built using Azure Serverless services like Logic Apps,…

PHP的静态变量介绍
静态变量只存在于函数作用域内,也就是说,静态变量只存活在栈中。一般的函数内变量在函数结束后会释放,比如局部变量,但是静态变量却不会。就是说,下次再调用这个函数的时候,该变量的值会保留下来。 只要在变…
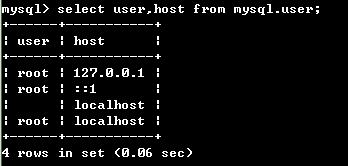
MySQL 解压版创建用户密码
root 权限进入MySQL: mysql –uroot 查看当前MySQL用户: select user,host from mysql.user; 此处以User为root,Host为localhost的账户为例,将密码改为password的命令: SET PASSWORD FOR rootlocalhost PASSWORD(newp…

git 忽略指定文件夹的上传
我们在使用 git 开发的时候,有些插件的模块文件通过npm install 就可以下载,一般是不上传到 git 中的(因为文件太多会导致很耗时),例如 我的 node_modules 文件夹,不想上传,我们应该这么做。 我们需要创建一…

数据库初学者_面向初学者的免费6小时数据科学课程
数据库初学者Data science is considered the "sexiest job of the 21st century." Learn data science in this full 6-hour course for absolute beginners from Barton Poulson of datalab.cc.数据科学被认为是“ 21世纪最艰巨的工作”。 通过datalab.cc的 Barton…

网页抓取及下载
downAndroidApk.php <?php /* 命令行 d: cd ApacheServer\php php.exe D:\ApacheServer\web\crawl\downAndroidApk.php --appidFileD:\ApacheServer\web\crawl\youxi.txt --newDirD:\ApacheServer\web\crawl\requestNewDir*/ // 判断必须在php-cli模式下运行,即…

javascript中关于this指向问题详解
前 言 LiuDaP 在前端的学习中,我们必然要用到js,js可以说是前端必不可少的的东西。在学习js的过程中,我们会经常用到this这个东西,而this的指向问题就变得尤为重要。今天正好有空闲时间,就给大家详细介绍一下js中关于…
mpvue 转uniapp 导航栏样式错乱问题修复 tabbar 样式修复
效果图:修改前,修改后 找了半天没找到原因,只能自己改样式了,下面是样式代码(在app.vue 里面加上就行) <style>/*每个页面公共css */uni-tabbar {box-sizing: border-box;position: fixed;left: 0;bo…

css规则_CSS规则,将使您的生活更轻松
css规则by Nick Gard尼克加德(Nick Gard) CSS规则,将使您的生活更轻松 (CSS rules that will make your life easier) After years of writing and maintaining a couple of very large web projects and numerous smaller ones, I have developed some heuristics…

在mybatis中模糊查询有三种写法
<select id"selectStudentsByName" resultType"Student"> <!--第一种--> <!-- select id,name,age,score from student where name like % #{0} % --> <!--第二种--> <!-- select id,name,age,score from student wher…

BZOJ 3566: [SHOI2014]概率充电器
题目:http://www.lydsy.com/JudgeOnline/problem.php?id3566 首先这题正着想不好想,考虑补集转化。 先dfs一遍,令f[u](1-p[u])*∏(1-(1-f[v])*w) f[u]表示u这个点通过其子树并不能联通的概率。 然后考虑v从其父亲连过来的情况,设…
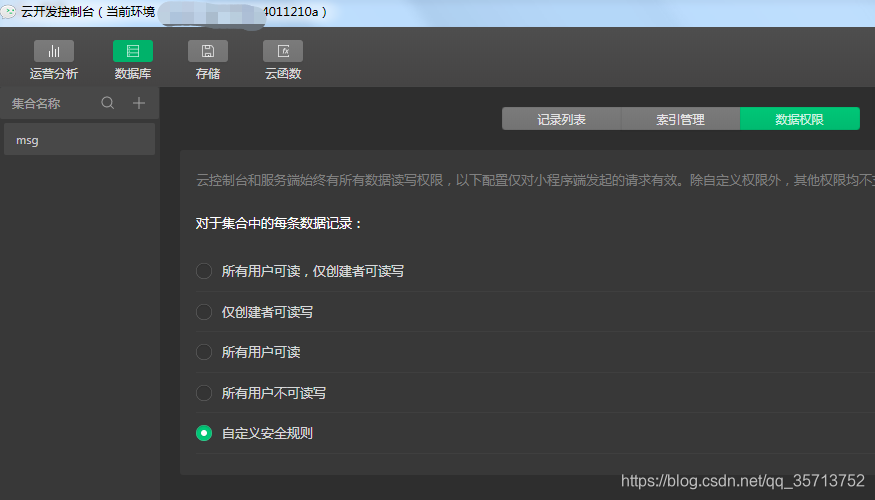
小程序云开发,订阅消息定时批量发送实现代码
需求:做一个类似抽奖结果通知的订阅消息提醒 实现流程: 每个用户需要先授权订阅消息接收,授权成功后把数据存到云开发的数据集合里面,再写个定时器,遍历数据集合的所有数据,拿到后遍历发送订阅消息&#…

机器学习速成课程
Learn the basics of machine learning and data science in this crash course tutorial for beginners from AI Sciences Academy. This course will give you the foundation you need to start learning more advanced material.在此速成课程教程中为AI Sciences Academy的…

H5 画布解决跨域问题,画布保存为图片显示在页面上
实现功能:uniapp H5 使用画布,绘画完之后保存为图片全屏显示完整实现代码,跨域解决方案。 跨域图片解决方案一:(使用base64编码)网络图片放到画布里面绘画 跨域图片解决方案二:(使…
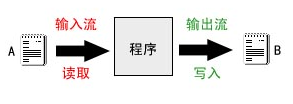
1、IO输入输出流 简介
IO流的分类: * 流向: * 输入流 读取数据 * 输出流 写出数据 * 数据类型: * 字节流 * 字节输入流 读取数据 InputStream * 字节输出流 写出数据 OutputStream * 字符流 * 字符输入流 读取数据 Reader * 字符输出流 写出数据 Writer * * 注意&…

mern技术栈好处?_通过构建运动追踪器应用程序来学习MERN堆栈(MERN教程)
mern技术栈好处?The MERN stack is a popular stack of technologies for building a modern single-page application. In this video course I developed, you will learn the MERN stack by building a full stack exercise tracker application.MERN堆栈是用于构建现代单页…
