二进制搜索树_二进制搜索树数据结构举例说明
二进制搜索树
A tree is a data structure composed of nodes that has the following characteristics:
树是由具有以下特征的节点组成的数据结构:
- Each tree has a root node (at the top) having some value.每棵树都有一个具有某些值的根节点(在顶部)。
- The root node has zero or more child nodes.根节点具有零个或多个子节点。
- Each child node has zero or more child nodes, and so on. This create a subtree in the tree. Every node has it’s own subtree made up of his children and their children, etc. This means that every node on its own can be a tree.每个子节点都有零个或多个子节点,依此类推。 这将在树中创建一个子树。 每个节点都有自己的子树,该子树由其子代及其子代组成。这意味着每个节点自身都可以是一棵树。
A binary search tree (BST) adds these two characteristics:
二进制搜索树(BST)添加了以下两个特征:
- Each node has a maximum of up to two children.每个节点最多有两个子节点。
- For each node, the values of its left descendent nodes are less than that of the current node, which in turn is less than the right descendent nodes (if any).对于每个节点,其左后代节点的值小于当前节点的值,而当前节点又小于右后代节点的值(如果有)。
The BST is built up on the idea of the binary search algorithm, which allows for fast lookup, insertion and removal of nodes. The way that they are set up means that, on average, each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree, O(log n).
BST建立在二进制搜索算法的基础上,该算法允许快速查找,插入和删除节点。 设置它们的方式意味着,平均而言,每个比较操作都可以跳过树的大约一半,因此每次查找,插入或删除操作所花费的时间与树中存储的项目数的对数成正比, O(log n) 。
However, some times the worst case can happen, when the tree isn’t balanced and the time complexity is O(n) for all three of these functions. That is why self-balancing trees (AVL, red-black, etc.) are a lot more effective than the basic BST.
但是,有时会发生最坏的情况,即树不平衡且所有这三个函数的时间复杂度均为O(n) 。 这就是为什么自平衡树(AVL,红黑色等)比基本BST更有效的原因。
Worst case scenario example: This can happen when you keep adding nodes that are always larger than the node before (it’s parent), the same can happen when you always add nodes with values lower than their parents.
最坏的情况示例:当您添加的节点总是大于之前的节点(它的父节点)时,可能会发生这种情况;当您添加值始终小于其父节点的节点时,也会发生这种情况。
BST的基本操作 (Basic operations on a BST)
- Create: creates an empty tree.创建:创建一个空树。
- Insert: insert a node in the tree.插入:在树中插入一个节点。
- Search: Searches for a node in the tree.搜索:在树中搜索节点。
- Delete: deletes a node from the tree.删除:从树中删除节点。
创造 (Create)
Initially an empty tree without any nodes is created. The variable/identifier which must point to the root node is initialized with a NULL value.
最初会创建一个没有任何节点的空树。 必须指向根节点的变量/标识符使用NULL值初始化。
搜索 (Search)
You always start searching the tree at the root node and go down from there. You compare the data in each node with the one you are looking for. If the compared node doesn’t match then you either proceed to the right child or the left child, which depends on the outcome of the following comparison: If the node that you are searching for is lower than the one you were comparing it with, you proceed to to the left child, otherwise (if it’s larger) you go to the right child. Why? Because the BST is structured (as per its definition), that the right child is always larger than the parent and the left child is always lesser.
您总是开始在根节点上搜索树,然后从那里向下走。 您将每个节点中的数据与要查找的节点进行比较。 如果比较的节点不匹配,那么您将继续选择右边的子节点还是左边的子节点,这取决于以下比较的结果:如果您要搜索的节点比您要比较的节点低,您将转到左侧的孩子,否则(如果较大)将转到右侧的孩子。 为什么? 因为BST是结构化的(按照其定义),所以右孩子总是比父孩子大,而左孩子总是小。
插 (Insert)
It is very similar to the search function. You again start at the root of the tree and go down recursively, searching for the right place to insert our new node, in the same way as explained in the search function. If a node with the same value is already in the tree, you can choose to either insert the duplicate or not. Some trees allow duplicates, some don’t. It depends on the certain implementation.
它与搜索功能非常相似。 您再次从树的根开始,然后递归地向下搜索,以与搜索功能中所述相同的方式搜索插入我们新节点的正确位置。 如果树中已经存在具有相同值的节点,则可以选择是否插入重复项。 有些树允许重复,有些则不允许。 这取决于特定的实现。
删除 (Delete)
There are 3 cases that can happen when you are trying to delete a node. If it has,
当您尝试删除节点时,可能会发生3种情况。 如果有的话
- No subtree (no children): This one is the easiest one. You can simply just delete the node, without any additional actions required.无子树(无子树):这是最简单的树。 您只需删除节点即可,而无需任何其他操作。
- One subtree (one child): You have to make sure that after the node is deleted, its child is then connected to the deleted node’s parent.一个子树(一个子树):您必须确保在删除节点后,将其子树连接到已删除节点的父树。
- Two subtrees (two children): You have to find and replace the node you want to delete with its successor (the letfmost node in the right subtree).两个子树(两个子树):必须找到要删除的节点并将其替换为其后继节点(右侧子树中的letfmost节点)。
The time complexity for creating a tree is O(1). The time complexity for searching, inserting or deleting a node depends on the height of the tree h, so the worst case is O(h).
创建树的时间复杂度为O(1) 。 搜索,插入或删除节点的时间复杂度取决于树h的高度,因此最坏的情况是O(h) 。
节点的前身 (Predecessor of a node)
Predecessors can be described as the node that would come right before the node you are currently at. To find the predecessor of the current node, look at the right-most/largest leaf node in the left subtree.
前任节点可以描述为您当前所在节点之前的节点。 要查找当前节点的前任节点,请查看左侧子树中最右侧/最大的叶节点。
节点的后继者 (Successor of a node)
Successors can be described as the node that would come right after the node you are currently at. To find the successor of the current node, look at the left-most/smallest leaf node in the right subtree.
继任者可以描述为您当前所在节点之后的节点。 要查找当前节点的后继节点,请查看右侧子树中最左侧/最小的叶节点。
特殊类型的BT (Special types of BT)
- Heap堆
- Red-black tree红黑树
- B-treeB树
- Splay tree八叉树
- N-ary treeN元树
- Trie (Radix tree)特里(基数树)
运行 (Runtime)
数据结构:数组 (Data structure: Array)
Worst-case performance:
O(log n)最坏情况下的性能:
O(log n)Best-case performance:
O(1)最佳情况下的性能:
O(1)Average performance:
O(log n)平均表现:
O(log n)Worst-case space complexity:
O(1)最坏情况下的空间复杂度:
O(1)
Where n is the number of nodes in the BST.
其中n是BST中的节点数。
实施BST (Implementation of BST)
Here’s a definiton for a BST node having some data, referencing to its left and right child nodes.
这是具有一些数据的BST节点的定义,参考其左子节点和右子节点。
struct node {int data;struct node *leftChild;struct node *rightChild;
};搜索操作 (Search Operation)
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
每当要搜索元素时,都从根节点开始搜索。 然后,如果数据小于键值,则在左侧子树中搜索元素。 否则,在右子树中搜索该元素。 每个节点遵循相同的算法。
struct node* search(int data){struct node *current = root;printf("Visiting elements: ");while(current->data != data){if(current != NULL) {printf("%d ",current->data);//go to left treeif(current->data > data){current = current->leftChild;}//else go to right treeelse { current = current->rightChild;}//not foundif(current == NULL){return NULL;}} }return current;
}插入操作 (Insert Operation)
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
每当要插入元素时,请先找到其正确位置。 从根节点开始搜索,然后如果数据小于键值,则在左侧子树中搜索空位置并插入数据。 否则,请在右侧子树中搜索空白位置并插入数据。
void insert(int data) {struct node *tempNode = (struct node*) malloc(sizeof(struct node));struct node *current;struct node *parent;tempNode->data = data;tempNode->leftChild = NULL;tempNode->rightChild = NULL;//if tree is emptyif(root == NULL) {root = tempNode;} else {current = root;parent = NULL;while(1) { parent = current;//go to left of the treeif(data < parent->data) {current = current->leftChild; //insert to the leftif(current == NULL) {parent->leftChild = tempNode;return;}}//go to right of the treeelse {current = current->rightChild;//insert to the rightif(current == NULL) {parent->rightChild = tempNode;return;}}} }
}Binary search trees (BSTs) also give us quick access to predecessors and successors. Predecessors can be described as the node that would come right before the node you are currently at.
二进制搜索树(BST)也使我们可以快速访问前任和后继。 先前的节点可以描述为您当前所在节点之前的节点。
- To find the predecessor of the current node, look at the rightmost/largest leaf node in the left subtree. Successors can be described as the node that would come right after the node you are currently at.要查找当前节点的前任节点,请查看左侧子树中最右侧/最大的叶节点。 继任者可以描述为您当前所在节点之后的节点。
- To find the successor of the current node, look at the leftmost/smallest leaf node in the right subtree.要查找当前节点的后继节点,请查看右侧子树中最左侧/最小的叶节点。
让我们看一下在树上运行的几个过程。 (Let’s look at a couple of procedures operating on trees.)
Since trees are recursively defined, it’s very common to write routines that operate on trees that are themselves recursive.
由于树是递归定义的,因此编写对本身是递归的树进行操作的例程非常普遍。
So for instance, if we want to calculate the height of a tree, that is the height of a root node, We can go ahead and recursively do that, going through the tree. So we can say:
因此,例如,如果我们要计算树的高度(即根节点的高度),则可以继续并递归地遍历树。 所以我们可以说:
- For instance, if we have a nil tree, then its height is a 0.例如,如果我们有一棵零树,那么它的高度是0。
- Otherwise, We’re 1 plus the maximum of the left child tree and the right child tree.否则,我们为1加上左子树和右子树的最大值。
So if we look at a leaf for example, that height would be 1 because the height of the left child is nil, is 0, and the height of the nil right child is also 0. So the max of that is 0, then 1 plus 0.
因此,例如,如果查看一片叶子,则该高度将为1,因为左子级的高度为nil,为0,而nil右级子级的高度也为0。因此,该最大值为0,则为1加0。
高度(树)算法 (Height(tree) algorithm)
if tree = nil:
return 0
return 1 + Max(Height(tree.left),Height(tree.right))这是C ++中的代码 (Here is the code in C++)
int maxDepth(struct node* node)
{if (node==NULL)return 0;else{int rDepth = maxDepth(node->right);int lDepth = maxDepth(node->left);if (lDepth > rDepth){return(lDepth+1);}else{return(rDepth+1);}}
}We could also look at calculating the size of a tree that is the number of nodes.
我们还可以查看计算树的大小(即节点数)。
- Again, if we have a nil tree, we have zero nodes.同样,如果我们有一个零树,那么我们有零个节点。
Otherwise, we have the number of nodes in the left child plus 1 for ourselves plus the number of nodes in the right child. So 1 plus the size of the left tree plus the size of the right tree.
否则,我们得到左子节点中的节点数加上自己的1,再加上右子节点中的节点数。 所以1加左树的大小再加上右树的大小。
大小(树)算法 (Size(tree) algorithm)
if tree = nil
return 0
return 1 + Size(tree.left) + Size(tree.right)这是C ++中的代码 (Here is the code in C++)
int treeSize(struct node* node)
{if (node==NULL)return 0;elsereturn 1+(treeSize(node->left) + treeSize(node->right));
}freeCodeCamp YouTube频道上的相关视频 (Relevant videos on freeCodeCamp YouTube channel)
Binary Search Tree
二进制搜索树
Binary Search Tree: Traversal and Height
二进制搜索树:遍历和高度
以下是二叉树的常见类型: (Following are common types of Binary Trees:)
Full Binary Tree/Strict Binary Tree: A Binary Tree is full or strict if every node has exactly 0 or 2 children.
完整的二叉树/严格的二叉树:如果每个节点恰好具有0或2个子节点,则二叉树是完整的或严格的。
18/ \ 15 30 / \ / \40 50 100 40In Full Binary Tree, number of leaf nodes is equal to number of internal nodes plus one.
在完整二叉树中,叶节点数等于内部节点数加一。
Complete Binary Tree: A Binary Tree is complete Binary Tree if all levels are completely filled except possibly the last level and the last level has all keys as left as possible
完整的二叉树:如果所有级别都已完全填充,则二叉树就是完整的二叉树,除了最后一个级别,并且最后一个级别的所有键都尽可能保留
18/ \ 15 30 / \ / \40 50 100 40/ \ /
8 7 9翻译自: https://www.freecodecamp.org/news/binary-search-tree-what-is-it/
二进制搜索树
相关文章:

无序数组及其子序列的相关问题研究
算法中以数组为研究对象的问题是非常常见的. 除了排序大家经常会遇到之外, 数组的子序列问题也是其中的一大分类. 今天我就对自己经常遇到的无序数组的子序列相关问题在这里总结一下. 前置条件: 给定无序数组. 以下所以的问题均以此为前置条件. 例如无序数组nums [2, 1, 3]. 问…

IOS使用正则表达式去掉html中的标签元素,获得纯文本
IOS使用正则表达式去掉html中的标签元素,获得纯文本 content是根据网址获得的网页源码字符串 NSRegularExpression *regularExpretion[NSRegularExpression regularExpressionWithPattern:"<[^>]*>|\n"options:0error:nil];content[regularExpretion string…

苹果禁止使用热更新 iOS开发程序员新转机来临
今天本是女神们的节日,所有iOS程序员沸腾了!原因是苹果爸爸发狠了,部分iOS开发者收到了苹果的这封警告邮件: [图一 苹果邮件] 消息一出,一时间众多开发者众说纷纭,以下是来源于网络的各种看法:…

Python中的Lambda表达式
Lambda表达式 (Lambda Expressions) Lambda Expressions are ideally used when we need to do something simple and are more interested in getting the job done quickly rather than formally naming the function. Lambda expressions are also known as anonymous funct…
JAVA-初步认识-第十一章-object类-equals方法覆盖
一. 现在要谈论equals方法另一个方面。如果不写equals方法,直接用来比较也是可以的,貌似equals方法有点多余。 现在不比较对象是否相等,而是比较对象中的特定内容,比如说对象的年龄,之前的写法如下 其实这个方法写完后…

JPPhotoBrowserDemo--微信朋友圈浏览图片
JPPhotoBrowserDemo Browse picture like WeChat. GithubDemo 使用 CocoaPods pod JPPhotoBrowser 在使用的页面中 引用 #import "JPPhotoBrowserManager.h"下载使用 直接将下载文件中的 JPPhotoBrowser 文件夹拖入项目中在使用的页面中 引用 #import "JPPhot…

STM32F103 与 STM32F407引脚兼容问题
突袭网收集的解决方案如下 解决方案1: STM32F103有的功能407都有,并且这些功能的引脚完全兼容,只是程序不同而已。。。而STM32F407有的功能103不一定有,因为407强大些。。。。。。希望对你有用 解决方案2: 不能。407支…

getdate函数_SQL日期函数和GETDATE解释为带有语法示例
getdate函数There are 61 Date Functions defined in MySQL. Don’t worry, we won’t review them all here. This guide will give you an introduction to some of the common ones, and enough exposure for you to comfortably to explore on your own.MySQL中定义了61种日…

JPTagView-多样化的标签View
JPTagView Customized tag pages GitHubDemo 使用 CocoaPods pod JPTagView 在使用的页面中 引用 #import "JPTagView.h"下载使用 直接将下载文件中的 JPTagView 文件夹拖入项目中在使用的页面中 引用 #import "JPTagView.h"使用方法见demo

zsh 每次打开Terminal都需要source bash_profile问题
zsh 每次打开Terminal都需要source bash_profile问题 zsh加载的是 ~/.zshrc文件,而 ‘.zshrc’ 文件中并没有定义任务环境变量。 解决办法,在~/.zshrc文件最后,增加一行: source .bash_profile alias alias gs"git status&q…

解析json实例
解析项目目录中的一个json文件,将之转化为List的一个方法。 package com.miracles.p3.os.util;import com.miracles.p3.os.mode.VideoBean; import org.json.JSONArray; import org.json.JSONObject;import java.util.ArrayList; import java.util.List;/*** Create…
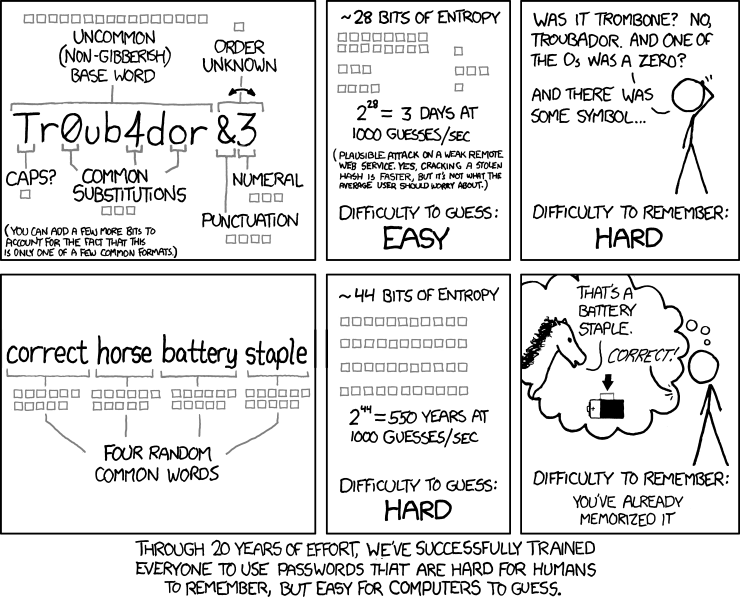
创建bdlink密码是数字_如何创建实际上是安全的密码
创建bdlink密码是数字I am very tired of seeing arbitrary password rules that are different for every web or mobile app. Its almost like these apps arent following a standard and are just making up their own rules that arent based on good security practices.…

通过分离dataSource 让我们的code具有更高的复用性.
转载自汪海的实验室 一 定义dataSource dataSource.h[objc] view plaincopytypedef void (^TableViewCellConfigureBlock)(id cell, id item); interface GroupNotificationDataSource : NSObject<UITableViewDataSource> - (id)initWithItems:(NSArray *)anItems …

复习心得 JAVA异常处理
java中的异常处理机制主要依赖于try,catch,finally,throw,throws五个关键字。其中, try关键字后紧跟一个花括号括起来的代码块(花括号不可省略)简称为try块。里面放置可能发生异常的代码。 catc…

Linux下Shell重定向
1. 标准输入,标准输出与标准错误输出 Linux下系统打开3个文件,标准输入,标准输出,标准错误输出。 标准输入:从键盘输入数据,即从键盘读入数据。 标准输出:把数据输出到终端上。 标准错误输出:把标准错误输出到终端上。…

sql avg函数使用格式_SQL AVG-SQL平均函数用语法示例解释
sql avg函数使用格式什么是SQL平均(AVG)函数? (What is the SQL Average (AVG) Function?) “Average” is an Aggregate (Group By) Function. It’s used to calculate the average of a numeric column from the set of rows returned by a SQL statement.“平均…

qml学习笔记(二):可视化元素基类Item详解(上半场anchors等等)
原博主博客地址:http://blog.csdn.net/qq21497936本文章博客地址:http://blog.csdn.net/qq21497936/article/details/78516201 qml学习笔记(二):可视化元素基类Item详解(上半场anchors等等) 本学章节笔记主要详解Item元…

使用PowerShell登陆多台Windows,测试DCAgent方法
目标: 需要1台PC用域账户远程登陆10台PC,每台登陆后的PC执行发送敏感数据的操作后,再logoff。 在DCAgent服务器上,查看这10个用户每次登陆时,DCAgent是否能获取到登陆信息(IP:User) …

优雅地分离tableview回调
你是否遇到过这样的需求,在tableview中显示一列数据,点击某一个cell时,在此cell下显示相应的附加信息。如下图:你是不是觉得需求很容易实现,只要使用tableview的insertRowsAtIndexPaths:withRowAnimation:插入一个附加cell就可以了࿰…

next.js_Next.js手册
next.jsI wrote this tutorial to help you quickly learn Next.js and get familiar with how it works.我编写本教程是为了帮助您快速学习Next.js并熟悉其工作方式。 Its ideal for you if you have zero to little knowledge of Next.js, you have used React in the past,…

Redux 入门教程(一):基本用法
一年半前,我写了《React 入门实例教程》,介绍了 React 的基本用法。 React 只是 DOM 的一个抽象层,并不是 Web 应用的完整解决方案。有两个方面,它没涉及。代码结构组件之间的通信对于大型的复杂应用来说,这两方面恰恰…

Elasticsearch——Rest API中的常用用法
本篇翻译的是Elasticsearch官方文档中的一些技巧,是使用Elasticsearch必不可少的必备知识,并且适用于所有的Rest Api。 返回数据格式化 当在Rest请求后面添加?pretty时,结果会以Json格式化的方式显示。另外,如果添加?formatyaml…

Python几种主流框架
从GitHub中整理出的15个最受欢迎的Python开源框架。这些框架包括事件I/O,OLAP,Web开发,高性能网络通信,测试,爬虫等。 Django: Python Web应用开发框架Django 应该是最出名的Python框架,GAE甚至Erlang都有框…

Git Fetch vs Pull:Git Fetch和Git Pull命令之间有什么区别?
Git pull and fetch are two commands that are regularly used by Git users. Let’s see the difference between both commands.Git pull和fetch是Git用户经常使用的两个命令。 让我们看看两个命令之间的区别。 For the sake of context, it’s worth remembering that we’…

Redux 入门教程(二):中间件与异步操作
上一篇文章,我介绍了 Redux 的基本做法:用户发出 Action,Reducer 函数算出新的 State,View 重新渲染。但是,一个关键问题没有解决:异步操作怎么办?Action 发出以后,Reducer 立即算出…
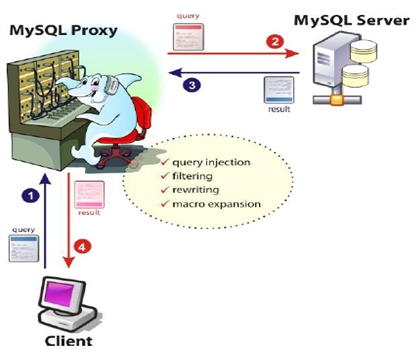
day09_读写分离_组件介绍
mysql中间件研究(Mysql-prxoy,Atlas,阿米巴,cobar,TDDL)mysql-proxyMySQL Proxy就是这么一个中间层代理,简单的说,MySQL Proxy就是一个连接池,负责将前台应用的连接请求转…
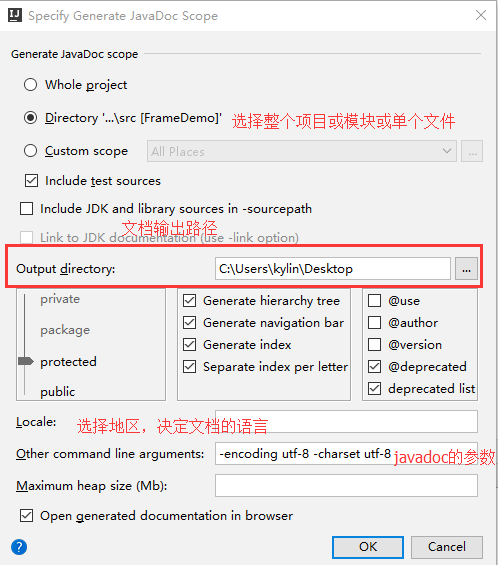
Idea其他设置
一、生成javadoc Tools->Gerenate JavaDoc 1. 选择是整个项目还是模块还是单个文件 2. 文档输出路径 3. Locale 选择地区,这个决定了文档的语言,中文就是zh_CN 4. 传入JavaDoc的参数,一般这样写 -encoding UTF-8 -charset UTF-8 -windowti…

freecodecamp_常见技术支持问题– freeCodeCamp常见问题解答
freecodecamp问题:我刚刚登录我的帐户,但看不到过去的任何进展。 (Question: I just signed into my account and I dont see any of my past progress.) Answer: You have created a duplicate account. Sign out of your account and try signing in u…
Redux 入门教程(三):React-Redux 的用法
前两篇教程介绍了 Redux 的基本用法和异步操作,今天是最后一部分,介绍如何在 React 项目中使用 Redux。 为了方便使用,Redux 的作者封装了一个 React 专用的库 React-Redux,本文主要介绍它。 这个库是可以选用的。实际项目中&…

SDN第二次上机作业
1、安装floodlight 2、生成拓扑并连接控制器floodlight,利用控制器floodlight查看图形拓扑 3、利用字符界面下发流表,使得‘h1’和‘h2’ ping 不通 4、利用字符界面下发流表,通过测试‘h1’和‘h3’的联通性,来验证openflow的har…
