n个集合 m个操作 操作: 1 a b 合并a,b所在集合 2 k 回到第k次操作之后的状态(查询算作操作) 3 a b 询问a,b是否属于同一集合,是则输出1否则输出0
0<n,m<=2*10^5 强制在线。
这两题一题都一样,另一题比较水,nm只有2*10^4,允许离线.....
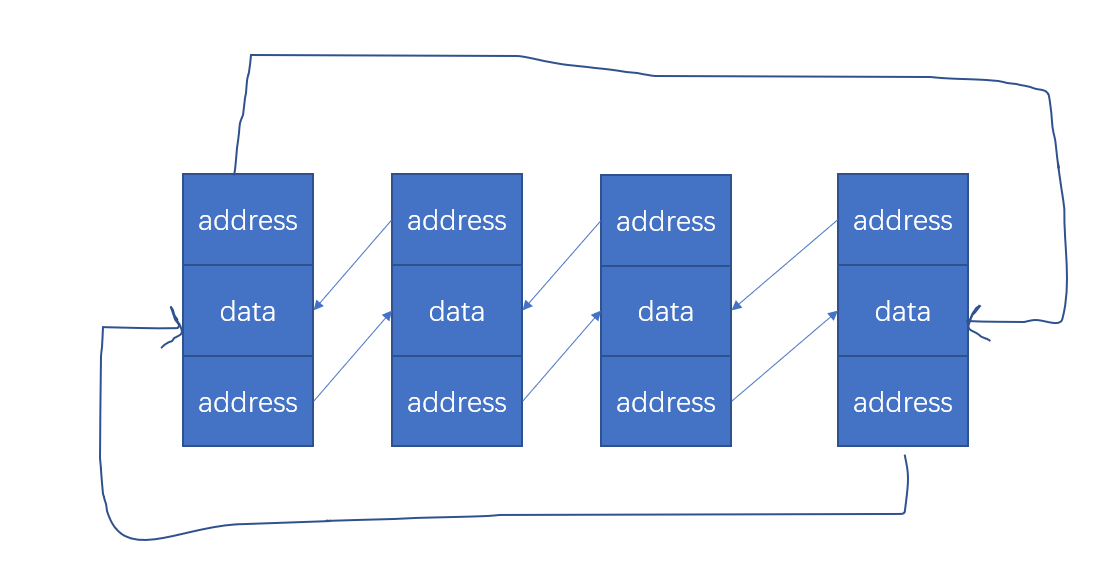
做法很简单,把数组当作可持久化线段树那么维护,每个表示区间的节点都不存东西,每次只要新建log个节点。
我交水的那道过不去,绝望的时候我交了一发加强版居然A了,根据我多年的经验一定是有特殊数据的坑,特判了一波终于过了。
用了启发式合并之后复杂度nlog^2n
#include<iostream> #include<cstdio> #define MN 20000000 #define MM 200000 using namespace std; inline int read() {int x = 0 , f = 1; char ch = getchar();while(ch < '0' || ch > '9'){ if(ch == '-') f = -1; ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f; }int cnt=0,n,m,last=0,rt[MM+5],cc; struct data{int x,size; }s[MM*3+5]; struct TREE{int l,r;data *x; }T[MN];void build(int x,int l,int r) {if(l==r){T[x].x=&s[l];return;}int mid=l+r>>1;build(T[x].l=(++cnt),l,mid);build(T[x].r=(++cnt),mid+1,r); }data*get(int x,int k,int l=1,int r=n) { if(l==r)return T[x].x;int mid=l+r>>1;if(k<=mid) return get(T[x].l,k,l,mid);else return get(T[x].r,k,mid+1,r); }data getfa(int x,int r) {data y=*get(r,x),ans=y;if(!y.x)return (data){x,ans.size};while(y.x) {ans=y;y=*get(r,y.x);}return (data){ans.x,y.size}; }void ins(int x,int dep,int k) {int l=1,r=n;int nx=rt[dep]=++cnt;while(l<r){int mid=l+r>>1;if(k<=mid){T[nx].r=T[x].r;T[nx].l=++cnt;nx=T[nx].l;x=T[x].l;r=mid;}else{T[nx].l=T[x].l;T[nx].r=++cnt;nx=T[nx].r;x=T[x].r;l=mid+1;}}T[nx].x=&s[cc]; }int main() {cc=n=read();m=read();for(int i=1;i<=n;i++)s[i]=(data){0,1};build(++cnt,1,n);rt[0]=1;for(int i=1;i<=m;i++){int a=read(),b=read()^last;if(a==2)rt[i]=rt[b];else{int c=read()^last;if(a==3) printf("%d\n",last=(getfa(b,rt[i-1]).x==getfa(c,rt[i-1]).x)),rt[i]=rt[i-1];else{data x=getfa(b,rt[i-1]),y=getfa(c,rt[i-1]);if(x.x==y.x){rt[i]=rt[i-1];continue;}if(x.size>y.size)swap(x,y);s[++cc]=(data){y.x,x.size};ins(rt[i-1],i,x.x);s[++cc]=(data){0,x.size+y.size};ins(rt[i],i,y.x);}}}return 0; }