当前位置：首页 > 编程日记 > 正文

递归/回溯：八皇后问题N-Queens

编程日记 2024-04-20 01:30:00

N皇后问题是计算机科学中最为经典的问题之一，该问题可追溯到1848年，由国际西洋棋棋手马克斯·贝瑟尔于提出了8皇后问题。
将N个皇后放摆放在N*N的棋盘中，互相不可攻击，有多少种摆放方式，每种摆放方式具体是怎样的?

8皇后即 8*8的棋盘中，将8个皇后放置在棋盘上，且皇后之间无法俩俩攻击到对方。

关于国际象棋中皇后的实力：国际象棋棋局中实力最强的一种棋子，也是最容易被吃掉的棋子。后可横直斜走，且格数不限

类似4*4的棋盘上，有如下两种皇后的放置方法:

.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..

分析：
N*N的棋盘放置N个皇后，即至少每一行需要一个皇后；

将一个皇后放置到棋盘上之后，棋盘如何演变（一个皇后放到棋盘，她的影响区域为上，下，左，右，左上，左下，右上，右下）
针对每一个皇后，如何能够确认下一个皇后，以及下下一个皇后。。。直到能够放置N个皇后的棋盘分布？

针对问题一，我们可以实现如下算法：
针对棋盘打标:

void mark_queen(int x, int y, std::vector<std::vector<int> > &mark) {/*维护两个方向数组可以取到皇后的八个方向即可这里定义了const型是为了节省内存，即整个进程代码运行期间，此时的const两个数组是存放在常量内存区，且定义为了static，则整个代码仅仅会有一份拷贝*/static const int dx[] = {0,0,-1,1,-1,1,-1,1}; static const int dy[] = {-1,1,0,0,-1,-1,1,1}; if (x < 0 || x > mark.size() || y < 0 || y > mark.size()) {return ;}mark[x][y] = 1;for (int i = 0;i < mark.size(); ++i) {for (int j = 0;j < 8; ++j) {int new_x = x + i * dx[j];int new_y = y + i * dy[j];if (new_x >= 0 && new_x < mark.size() && new_y >= 0 && new_y < mark.size()) {mark[new_x][new_y] = 1;}}}
}

回到问题2上，我们想要获取棋盘上能够放置皇后的方法的个数以及具体的放置位置；
可以先尝试一个一个放，当然这放置可以按照行放，也可以按照列放（八皇后问题最终的表现形式就是每行只能有一个，每一列只能有一个）。
我们这里的放置皇后的方式都按照行放，第一行第一个：

Q	1	1	1
1	1	0	0
1	0	1	0
1	0	0	1

接下来皇后的放置的规则肯定就是在不能被第一个Q影响的情况下放置了，我们这里仍然按照行进行放置，放第二个,如下红色1则为重新放置后打入的标记

Q	1	1	1
1	1	Q	1
1	1	1	1
1	0	1	1

再次进行放置，发现第三行已经没有位置可以放了，此时可以定论，最开始的第一次放置位置不合理，需要进行回溯，回溯到第一次放置Q之前棋盘的位置，即

0	0	0	0
0	0	0	0
0	0	0	0
0	0	0	0

综上过程我们可以知道我们算法实现有以下几个点

按行（或者列）进行棋盘遍历，每一次放置一个皇后，并对皇后区域进行打标
以上过程需要递归完成，递归过程中发现无法达到N*N放置N个皇后时即终止递归，并回滚棋盘状态为第一次放置皇后之前的棋盘状态。

实现算法如下(文末有完整测试代码):

/*标记棋盘放置皇后的数组*/
void mark_queen(int x, int y, std::vector<std::vector<int> > &mark) {static const int dx[] = {0,0,-1,1,-1,1,-1,1};static const int dy[] = {-1,1,0,0,-1,-1,1,1};if (x < 0 || x > mark.size() || y < 0 || y > mark.size()) {return ;}mark[x][y] = 1;for (int i = 0;i < mark.size(); ++i) {for (int j = 0;j < 8; ++j) {int new_x = x + i * dx[j];int new_y = y + i * dy[j];if (new_x >= 0 && new_x < mark.size() && new_y >= 0 && new_y < mark.size()) {mark[new_x][new_y] = 1;}}}
}/*递归+回溯棋盘状态*/
void generate(int k, int n, std::vector<string> &location, //用字符表示放置策略std::vector<std::vector<string>> &result, //最终的放置策略的汇总std::vector<std::vector<int> > &mark) { //保存每一次放置皇后的棋盘状态if (k == n) { //结束条件就是发现当前放置策略支持N个皇后result.push_back(location);return;}/*按行遍历*/for (int i = 0;i < n; ++i) {/*备份初始棋盘状态*/std::vector<std::vector<int>> tmp_mark = mark;/*放置位置就是没有被打标的位置，即不会被其他皇后影响的位置*/if (mark[k][i] == 0) {/*放置一个皇后，针对其进行打标*/mark_queen(k, i, mark);location[k][i] = 'Q';generate(k+1, n, location, result, mark);/*递归之后回滚到最初备份的状态*/mark = tmp_mark;location[k][i] = '.';}}
}
/*初始化棋盘*/
std::vector<std::vector<string> > solve_N_queen(int n) {std::vector<std::vector<int> > mark;std::vector<std::vector<string> > result;std::vector<string> location;for (int i = 0;i < n; ++i) {mark.push_back(std::vector<int> ());for (int j = 0;j < n; ++j) {mark[i].push_back(0);}location.push_back("");location[i].append(n,'.');}generate(0,n,location,result,mark);return result;
}

测试代码如下:

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>/*
N皇后问题是计算机科学中最为经典的问题之一，该问题可追溯到1848年
由国际西洋棋棋手马克斯·贝瑟尔于提出了8皇后问题。 将N个皇后放摆放在N*N的棋盘中，互相不可攻击，有多少种摆放方式，每种摆 放方式具体是怎样的?类似 N = 4
那么如下输出
solution1:
.Q..
...Q
Q...
..Q.solution2:
..Q.
Q...
...Q
.Q..
*/using namespace std;/*标记棋盘放置皇后的数组*/
void mark_queen(int x, int y, std::vector<std::vector<int> > &mark) {static const int dx[] = {0,0,-1,1,-1,1,-1,1};static const int dy[] = {-1,1,0,0,-1,-1,1,1};if (x < 0 || x > mark.size() || y < 0 || y > mark.size()) {return ;}mark[x][y] = 1;for (int i = 0;i < mark.size(); ++i) {for (int j = 0;j < 8; ++j) {int new_x = x + i * dx[j];int new_y = y + i * dy[j];if (new_x >= 0 && new_x < mark.size() && new_y >= 0 && new_y < mark.size()) {mark[new_x][new_y] = 1;}}}
}void generate(int k, int n, std::vector<string> &location, std::vector<std::vector<string>> &result, std::vector<std::vector<int> > &mark) {if (k == n) {result.push_back(location);return;}for (int i = 0;i < n; ++i) {std::vector<std::vector<int>> tmp_mark = mark;if (mark[k][i] == 0) {mark_queen(k, i, mark);location[k][i] = 'Q';generate(k+1, n, location, result, mark);mark = tmp_mark;location[k][i] = '.';}}
}std::vector<std::vector<string> > solve_N_queen(int n) {std::vector<std::vector<int> > mark;std::vector<std::vector<string> > result;std::vector<string> location;for (int i = 0;i < n; ++i) {mark.push_back(std::vector<int> ());for (int j = 0;j < n; ++j) {mark[i].push_back(0);}location.push_back("");location[i].append(n,'.');}generate(0,n,location,result,mark);return result;
}int main(int argc, char const *argv[])
{int n;cin >> n;std::vector<std::vector<string>> result; result = solve_N_queen(n);cout << "num of method is " << result.size() << endl;cout << "method is " << endl;for (int i = 0; i < result.size(); ++i) {for (int j = 0;j < result[i].size(); ++j) {cout << result[i][j];cout << endl;}cout << endl;}return 0;
}

编译:g++ -std=c++11 test.c -o test

输出如下:

#输入
8
#输出
num of method is 92
method is 
Q.......
....Q...
.......Q
.....Q..
..Q.....
......Q.
.Q......
...Q....
#以下输出较多，可自行编译查看
...#输入
4
#输出
num of method is 2
method is 
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..

https://www.dkcj.cn/info/4937.html

KS103超声波测距模块

max232：电平转换芯片，将电脑的RS-232标准串口（高12V，低-12V）转换为（高5V，低0V）。电脑串口（RS -232） > 单片机串口（TTL串口） SIPEX…

编程日记2024/04/20 01:00:00

linux 硬盘操作,linux常用disk磁盘操作命令

编程日记2024/04/20 00:30:00

在Spring中采用声明式方法对Hibernate和JDBC进行统一的事务配置（AOP）

<?xml version"1.0" encoding"UTF-8"?><beans xmlns"http://www.springframework.org/schema/beans" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xmlns:aop"http://www.springframework.…

编程日记2024/04/20 00:00:00

Leetcode 213.大家劫舍II

打家劫舍II 你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房…

编程日记2024/04/19 23:30:00

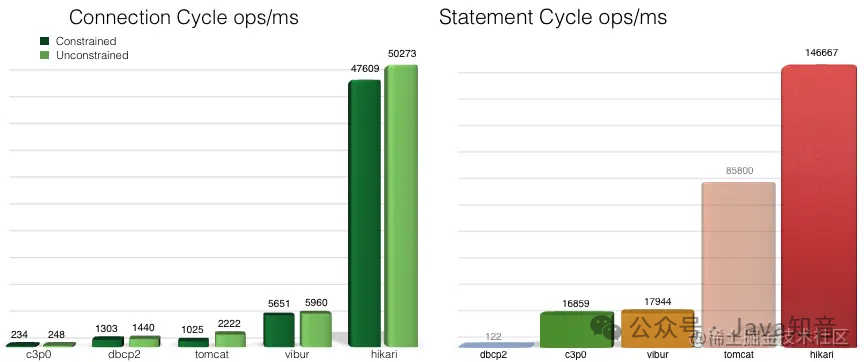
替代Druid，HakariCP 为什么这么快？

这次源码探究，真的感觉看到了无数个小细节，无数个小优化，积少成多。平时开发过程中，一些小的细节也一定要“扣”。

编程日记2024/04/19 23:00:02

递归/分治：归并排序

前言分治算法: 将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解后进行合并，就可得到原问题的解。步骤如下: 分解，将要解决的问题划分成若干规模较小的同类问题;求解，…

编程日记2024/04/19 23:00:00

Java中volatile 的使用场景有哪些？

volatile是一种轻量级的同步机制，它能保证共享变量的可见性，同时禁止重排序保证了操作的有序性，但是它无法保证原子性。所以使用volatilevolatile。

编程日记2024/04/19 22:30:05

Java 22 除了推出了新的增强功能和特性，也获得 Java Management Service (JMS) 的支持，这是一项新的 Oracle 云基础设施远程软件服务(Oracle Cloud Infrastructure, OCI) 原生服务，提供统一的控制台和仪表盘，帮助企业管理本地或云端的 Java 运行时和应用。使包含运行时计算值的字符串更容易表达，简化 Java 程序的开发工作，同时提高将用户提供的值编写成字符串，并将字符串传递给其他系统的程序的安全性。支持开发人员自由地表达构造器的行为。

编程日记2024/04/19 22:30:05

Jackson 用起来！

你可以创建自定义序列化器和反序列化器以自定义特定字段或类的序列化和反序列化行为。为此，请创建一个实现或接口的类，并在需要自定义的字段或类上使用和注解。@Override// ...其他代码...优势性能优异：Jackson在序列化和反序列化过程中表现出优秀的性能，通常比其他Java JSON库更快。灵活性：通过注解、自定义序列化器/反序列化器等功能，Jackson提供了丰富的配置选项，允许你根据需求灵活地处理JSON数据。易于使用：Jackson的API设计简洁明了，易于学习和使用。

编程日记2024/04/19 22:30:05

Swift中的问号?和感叹号!

Swift语言使用var定义变量，但和别的语言不同，Swift里不会自动给变量赋初始值，也就是说变量不会有默认值，所以要求使用变量之前必须要对其初始化。如果在使用变量之前不进行初始化就会报错： var stringValue : String …

编程日记2024/04/19 22:30:00

拜托！别再滥用 ! = null 判空了！！

另外，也许受此习惯影响，他们总潜意识地认为，所有的返回都是不可信任的，为了保护自己程序，就加了大量的判空。如果你养成习惯，都是这样写代码（返回空collections而不返回null)，你调用自己写的方法时，就能大胆地忽略判空）这种情况下，null是个”看上去“合理的值，例如，我查询数据库，某个查询条件下，就是没有对应值，此时null算是表达了“空”的概念。最终，项目中会存在大量判空代码，多么丑陋繁冗！，而不要返回null，这样调用侧就能大胆地处理这个返回，例如调用侧拿到返回后，可以直接。

编程日记2024/04/19 22:00:02

ffmpeg java linux水印,Linux环境用FFmpeg给视频加水印详细步骤

FFmpeg给视频添加水印，根据官方文档的介绍可以知道FFmpeg在编译安装的时候还需要加 –enable-libfreetype、–enable-libfontconfig、 --enable-libfribidi 这几个参数，而这几个组件又需要从外面编译安装，我看很多博主直接用FFmpeg命令加水印…

编程日记2024/04/19 22:00:00

red hat DHCP服务器配置

[ 基本操作 ] rpm –q dhcp / rpm -ql grep dhcp [ 查询DHCP ] yum –y install dhcp dhcp -devel service dhcpd start [ 启动 ] service dhcpd status [ 查看DHCP状态 ] chkconfig – level 3 5 dhcpd on [ 改变启动级别为3 5 自动启动服务 ] service ne…

编程日记2024/04/19 21:30:00

axios解决调用后端接口跨域问题

vue-cli通过是本地代理的方式解决接口跨域问题的。但是在vue-cli的默认项目配置中这个代理是没有配置的，如果现在项目中使用，必须手动配置config/index.js文件 ... proxyTable: {/api: { //将www.exaple.com印射为/apistarget: https://www.example.c…

编程日记2024/04/19 21:00:00

递归/归并：count of smaller numbers求逆序数

已知数组nums，求新数组count，count[i]代表了在nums[i]右侧且比 nums[i]小的元素个数。例如: nums [5, 2, 6, 1], count [2, 1, 1, 0]; nums [6, 6, 6, 1, 1, 1], count [3, 3, 3, 0, 0, 0]; nums [5, -7, 9, 1, 3, 5, -2, 1], count [5, 0, 5, 1…

编程日记2024/04/19 20:30:00

远程计划任务管理

有时你需要远程管理或运行一批机器，但是按要求你没有权限或者不能安装客户端，下面的批处理可能帮上你的忙，将下方代码保存为批处理，并创建Clients.txt，存放的是以回车分隔的IP echo off setlocal enabledelayedexpansi…

编程日记2024/04/19 20:00:00

linux shell for 循环变量,shell for循环总结

1 shell for循环语法for 变量 in 列表docommand1command2...commandNdone1.1 读取列表中的值#!/bin/bashfor test in apple boy cat dogdoecho The next state is $testdone结果：The next state is appleThe next state is boyThe next state is catThe next state …

编程日记2024/04/19 19:30:00

自定义堆栈（回文检测）

using System; using System.Collections;namespace CStack {class Program{static void Main(string[] args){CStack alist new CStack();string ch;string word "上海自来水来自海上";bool isPalindrome true;for (int x 0; x < word.Length; x){alist.Push…

编程日记2024/04/19 19:00:00

二叉树(C++)：创建，前中后序遍历（递归+非递归），获取叶子节点个数，获取树的高度

文章目录前言创建二叉树先序遍历中序遍历后序遍历获取叶子节点个数获取树的高度测试代码前言现有如下二叉树: 关于二叉树的相关操作，我们能够发现二叉树从根节点到子节点，以及每个中间节点基本都能够拆分为若干个子节点的操作，且每个子节点…

编程日记2024/04/19 18:30:00

6月11号=》121页-125页

6.1　　样式单概述 W3C已经给出了两种样式单语言的推荐标准，一种是级联样式单CSS(Cascading Style Sheets)， 另一种是可扩展样式单语言XSL(eXtensible Stylesheet Language)。 6.1.1　　CSS CSS主要提供如下两个功能： 1：对页面的字…

编程日记2024/04/19 18:00:00

linux cp sync,通过SSH使用Rsync传输文件，复制和同步文件及目录

在本文中，我们将解释如何通过SSH使用rsync复制文件。当涉及在网络上的系统之间传输文件时，Linux和Unix用户可以使用许多工具，最流行的数据传输协议是SSH和FTP，虽然FTP很受欢迎，但总是喜欢使用SSH，因为它是传…

编程日记2024/04/19 17:30:00

【Java笔记】C++与Java的对比

接口： C可以多重继承，而Java不可以。但是Java里一个类可以声明实现多个接口。

编程日记2024/04/19 17:00:00

cf792b循环链表

头尾链接一下就好， /* 1 2 3 4 5 6 7:4 5 6 7 1 2 3:2 3 5 6 7 1:5 6 7 1 3:6 7 1 3:1 3 7 */ #include<bits/stdc.h> using namespace std; int main(){int n,k,q[200],nxt[200],p,pre,tot;scanf("%d%d",&n,&k);for(int i1;i&…

编程日记2024/04/19 16:30:00

二叉树：路径之和 Path Sum

给定一个二叉树与整数sum，找出所有从根节点到叶结点的路径，这些路径上的节点值累加和为sum 即创建一个二叉树，要求二叉树中有一个路径从根节点到叶节点到路径加起来代表到和为给定的sum 如下二叉树给定路径之和为18，则需要输…

编程日记2024/04/19 16:00:00

从零开始编写自己的C#框架（16）——Web层后端父类

从零开始编写自己的C#框架（16）——Web层后端父类原文:从零开始编写自己的C#框架（16）——Web层后端父类本章节讲述的各个类是后端系统的核心之一，涉及到系统安全验证、操作日志记录、页面与按键权限控制、后端页面功能…

编程日记2024/04/19 15:30:00

c语言中的普通字符包括什么,【判断题】C语言中的字符常量通常有两种形式:普通字符和转义字符。...

【判断题】C语言中的字符常量通常有两种形式:普通字符和转义字符。更多相关问题－－－Can you speak French？－－－Yes, but only____.A．a littleB．littleC．muchD&a…

编程日记2024/04/19 15:00:00

Codeforces Round #104 (Div. 2) E DP(01背包模型) +组和+除法取模求逆元

题意： 规定只包含4或7的数为幸运数字，给定n个数的序列，求他的子序列，使得该子序列的长度为k并且满足该子序列中不存在相同的两个幸运数字。问一共寻在多少种可能。（只要该数的下标不同则认为是不同的序列） …

编程日记2024/04/19 14:30:00

django 增加验证邮箱功能

在user文件夹下新建python包，utils 在包内新建文件email_send.py,其中包括验证字符串随机码的产生，数据库的存储和email的发送 # -*- coding: utf-8 -*- # 作者：神秘藏宝室 # 日期：2019/1/1 22:21 from random import Random from…

编程日记2024/04/19 14:00:00

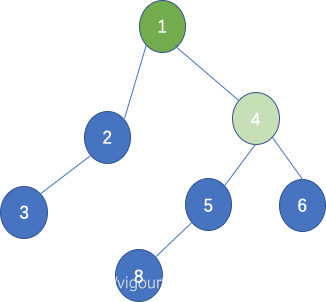
二叉树：最近的公共祖先 Lowest Common Ancestor of a Binary Tree

已知二叉树，求二叉树中给定的两个节点的最近公共祖先。最近公共祖先: 两节点v与w的最近公共祖先u，满足在树上最低(离根最远)，且v,w两个节点都是u的子孙。如上二叉树，6和8号节点的公共祖先有4，1；但是最近…

编程日记2024/04/19 13:30:00

VS不显示最近打开的项目

VS2012不显示最近打开的项目解决方法， 在"运行"中输入 " gpedit.msc"打开后在"用户配置"-"管理模板"-"任务栏和开始菜单" 然后将用户配置-->管理模板-->不保留最近打开文档的历史将此选项设置为禁用源…

编程日记2024/04/19 13:00:00

递归/回溯：八皇后问题N-Queens

相关文章：

KS103超声波测距模块

linux 硬盘操作,linux常用disk磁盘操作命令

在Spring中采用声明式方法对Hibernate和JDBC进行统一的事务配置（AOP）

Leetcode 213.大家劫舍II

替代Druid，HakariCP 为什么这么快？

递归/分治：归并排序

Java中volatile 的使用场景有哪些？

JDK22 正式发布了！

Jackson 用起来！

Swift中的问号?和感叹号!

拜托！别再滥用 ! = null 判空了！！

ffmpeg java linux水印,Linux环境用FFmpeg给视频加水印详细步骤

red hat DHCP服务器配置

axios解决调用后端接口跨域问题

递归/归并：count of smaller numbers求逆序数

远程计划任务管理

linux shell for 循环变量,shell for循环总结

自定义堆栈（回文检测）

二叉树(C++)：创建，前中后序遍历（递归+非递归），获取叶子节点个数，获取树的高度

6月11号=》121页-125页

linux cp sync,通过SSH使用Rsync传输文件，复制和同步文件及目录

【Java笔记】C++与Java的对比

cf792b循环链表

二叉树：路径之和 Path Sum

从零开始编写自己的C#框架（16）——Web层后端父类

c语言中的普通字符包括什么,【判断题】C语言中的字符常量通常有两种形式:普通字符和转义字符。...

Codeforces Round #104 (Div. 2) E DP(01背包模型) +组和+除法取模求逆元

django 增加验证邮箱功能

二叉树：最近的公共祖先 Lowest Common Ancestor of a Binary Tree

VS不显示最近打开的项目