二叉树(C++)：创建，前中后序遍历（递归+非递归），获取叶子节点个数，获取树的高度

前言

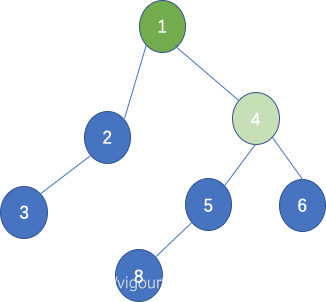
现有如下二叉树:

关于二叉树的相关操作，我们能够发现二叉树从根节点到子节点，以及每个中间节点基本都能够拆分为若干个子节点的操作，且每个子节点的操作都和其头节点操作一致。
所以我们针对二叉树的操作都可以使用分治算+回溯/归并算法进行

完整测试代码见文末

创建二叉树

二叉树数据结构:

typedef struct tree
{char data;struct tree *left;struct tree *right;
}Tree,*TreeNode;

我们使用先序方式，创建如上二叉树：
输入如下: ABD***CE**FG***
创建过程

/*创建二叉树*/
void createTree(TreeNode *root) {char val = 0;cin >> val; //持续输入，直到完成一个二叉树的构建if (val == '*') {//输入为*则代表当前节点为空(*root) = NULL;} else {(*root) = (Tree *)malloc(sizeof(tree));if ((*root) == NULL) {cout << "create node failed " << endl;exit(-1);} else {(*root)->data = val;//为输入的节点赋值createTree(&(*root)->left);//分治左孩子节点createTree(&(*root)->right);//分治右孩子节点}}
}

先序遍历

先序遍历二叉树指:先遍历二叉树的根节点，再遍历当前根节点所有左子树，再遍历当前根节点所有右子树

因为这个过程针对子节点的遍历和根节点是没有任何区别的，所以可以使用分治进行处理

/*递归先序遍历*/
void preOrder(Tree *root) {if (root == NULL) {return;}cout << root->data;preOrder(root->left);preOrder(root->right);
}

同样可以使用栈进行非递归的先序遍历,即
栈可以保存遍历过程中的左节点，因为先序遍历是先访问根节点，其次就是左节点

while(p) {cout << p ->data; //访问根节点s.push(p); //保存左子节点p = p->left;
}

接着再弹栈，直到获取一个右节点

while(!s.empty()) {p = s.top();s.pop();p = p -> right;
}

接着再重复对右节点进行同样的访问操作，具体过程如下

/*非递归先序遍历*/
void preOrderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;while(!s.empty() || p) {while(p) {cout << p ->data;s.push(p);p = p->left;}while(!s.empty()) {p = s.top();s.pop();p = p -> right;}}cout << endl;
}

中序遍历

中序遍历二叉树是指：先访问左节点，中间访问根节点，最后访问右节点
分治过程如下:

void inorder(Tree *root) {if (root == NULL) {return;}inorder(root -> left);cout << root -> data;inorder(root -> right);
}

中序遍历二叉树的非递归方式和先序类似，支持访问的时机是在先访问第一轮所有的左节点，再获取右节点之前进行根节点的访问，实现过程如下:

/*非递归中序遍历*/
void inorderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;while(!s.empty() || p) {while(p) {s.push(p);p = p ->left;}while(!s.empty()) {p = s.top();cout << p->data;s.pop();p = p->right;}}cout << endl;
}

后序遍历

后序遍历二叉树是指：先访问左节点，再访问右节点，最后访问根节点
分治过程如下:

/*递归后序遍历*/
void lastorder(Tree *root) {if (root == NULL) {return;}lastorder(root -> left);lastorder(root -> right);cout << root -> data;
}

非递归的访问过程和先序/中序遍历有差异，因为后序遍历需要优先访问完左节点、右节点
所以根节点的访问前提是：

1. 右子节点为空
2. 右子节点已经访问过

所以实现的过程中需要保存已经访问过的右子节点

void lastorderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;Tree *lastvisit = NULL;//保存已经访问过的右子节点/*先获取到左子节点*/while(p) {s.push(p);p = p ->left;}while(!s.empty()) {p = s.top();s.pop();/*右节点已经为空或者已经访问过，那么认为右节点已经访问完，可以访问根节点了*/if (p -> right == NULL || p ->right == lastvisit) {cout << p->data;lastvisit = p;} else {//否则，将右节点以及右节点的子节点入栈从而继续访问s.push(p);p = p -> right;/*每获取到一个非空右节点，就将该右节点的左节点放入栈中*/while(p) {s.push(p);p = p -> left;}}}cout << endl;
}

获取叶子节点个数

叶子节点的条件就是：左右子树都为空
此时返回值应该为1
分治+归并获取叶子节点的个数

int getLeavesNode(Tree *root) {if (root == NULL) {return 0;} else {if (root -> left == NULL && root ->right == NULL) {return 1;}return getLeavesNode(root -> left) + getLeavesNode(root -> right);}
}

获取树的高度

树的高度为左右子节点的 层数较大的一个数值
实现过程如下:

int heightTree(Tree *root) {int height = 0;if (root == NULL) {return 0;} else {int l_height = heightTree(root -> left);int r_height = heightTree(root -> right);height = l_height > r_height? l_height +1 :r_height+1;}return height;
}

测试代码

#include <iostream>
#include <stack>
#include <vector>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>using namespace std;typedef struct tree
{char data;struct tree *left;struct tree *right;
}Tree,*TreeNode;/*创建二叉树*/
void createTree(TreeNode *root) {char val = 0;cin >> val;if (val == '*') {(*root) = NULL;} else {(*root) = (Tree *)malloc(sizeof(tree));if ((*root) == NULL) {cout << "create node failed " << endl;exit(-1);} else {(*root)->data = val;createTree(&(*root)->left);createTree(&(*root)->right);}}
}/*递归先序遍历*/
void preOrder(Tree *root) {if (root == NULL) {return;}cout << root->data;preOrder(root->left);preOrder(root->right);
}/*非递归先序遍历*/
void preOrderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;while(!s.empty() || p) {while(p) {cout << p ->data;s.push(p);p = p->left;}while(!s.empty()) {p = s.top();s.pop();p = p -> right;}}cout << endl;}/*递归中序遍历*/
void inorder(Tree *root) {if (root == NULL) {return;}inorder(root -> left);cout << root -> data;inorder(root -> right);
}/*非递归中序遍历*/
void inorderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;while(!s.empty() || p) {while(p) {s.push(p);p = p ->left;}while(!s.empty()) {p = s.top();cout << p->data;s.pop();p = p->right;}}cout << endl;
}/*递归后序遍历*/
void lastorder(Tree *root) {if (root == NULL) {return;}lastorder(root -> left);lastorder(root -> right);cout << root -> data;
}void lastorderNoRecur(Tree *root) {if (root == NULL) {return;}stack<TreeNode> s;Tree *p = root;Tree *lastvisit = NULL;while(p) {s.push(p);p = p ->left;}while(!s.empty()) {p = s.top();s.pop();/*右节点已经为空或者已经访问过，那么认为右节点已经访问完，可以访问根节点了*/if (p -> right == NULL || p ->right == lastvisit) {cout << p->data;lastvisit = p;} else {//否则，将右节点以及右节点的子节点入栈从而继续访问s.push(p);p = p -> right;while(p) {s.push(p);p = p -> left;}}}cout << endl;
}int getLeavesNode(Tree *root) {if (root == NULL) {return 0;} else {if (root -> left == NULL && root ->right == NULL) {return 1;}return getLeavesNode(root -> left) + getLeavesNode(root -> right);}
}int heightTree(Tree *root) {int height = 0;if (root == NULL) {return 0;} else {int l_height = heightTree(root -> left);int r_height = heightTree(root -> right);height = l_height > r_height? l_height +1 :r_height+1;}return height;
}int main(int argc, char const *argv[])
{/* code */TreeNode root;cout << "construct the tree " << endl;createTree(&root);cout << "previous order recursion " << endl;preOrder(root);cout << "\nprevious order no recursion " << endl;preOrderNoRecur(root);cout << "inorder recursion " << endl;inorder(root);cout << "\ninorder no recursion " << endl;inorderNoRecur(root);cout << "lastorder recursion " << endl;lastorder(root);cout << "\nlastorder no recursion " << endl;lastorderNoRecur(root);cout << "height of the tree is " << heightTree(root) << endl;cout << "num leaves of the tree is " << getLeavesNode(root) << endl;return 0;
}

输出如下:

#输入
construct the tree 
ABD***CE**FG***
#输出
previous order recursion 
ABDCEFG
previous order no recursion 
ABDCEFG
inorder recursion 
DBAECGF
inorder no recursion 
DBAECGF
lastorder recursion 
DBEGFCA
lastorder no recursion 
DBEGFCA
height of the tree is 4
num leaves of the tree is 3