原题:ZOJ 3791 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3791
题意:给定两个0-1序列s1, s2,操作t次,每次改变m个位置,求把s1改变为s2的方法总数。
解法:
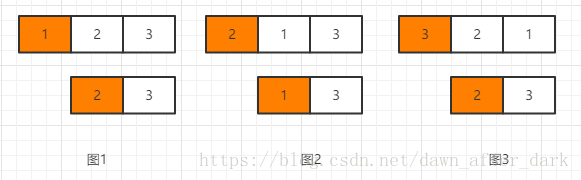
DP,s1和s2哪些位置相同并不重要,重要的是有几个位置不同。改变的时候也一样,改变哪些位置并不重要,重要的是改变之后有几个位置不同。当时就想到了这一点,后面就不知道怎么办了。
定义: dp[i][j]表示i次操作之后有j个位置不同的方法数,答案就是dp[k][0]。
对于dp[i-1][j],经过一次操作之后假设把x个位置从不同变为相同,剩下m-x个位置从相同变为不同,那么转移方程:
dp[i][j+m-x-x] += dp[i-1][j] * C(j, x) * C(n-j, m-x)
其中C(j, k)表示组合数,即从j个不同的位置选出k个改变。循环x即可。
代码:


#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <string> #define Mod 1000000009 #define ll long long using namespace std; #define N 107int c[N][N]; ll dp[N][N];void calc_C() {memset(c,0,sizeof(c));c[0][0] = 1;for(int i=1;i<=100;i++){c[i][0] = 1;for(int j=1;j<=i;j++)c[i][j] = (c[i-1][j-1] + c[i-1][j])%Mod;} }int main() {int n,s,m;int dif,i,j,k;string a,b;calc_C();while(scanf("%d%d%d",&n,&s,&m)!=EOF){cin>>a>>b;dif = 0;for(i=0;i<n;i++)if(a[i] != b[i])dif++;memset(dp,0,sizeof(dp));dp[0][dif] = 1;for(i=1;i<=s;i++){for(j=0;j<=n;j++){for(k=max(0,m-n+j);k<=j&&k<=m;k++){dp[i][j+m-k-k] += ((dp[i-1][j]*c[j][k])%Mod)*c[n-j][m-k]%Mod;dp[i][j+m-k-k] %= Mod;}}}printf("%lld\n",dp[s][0]);}return 0; }