转自:http://www.cnblogs.com/shengshouzhaixing/archive/2013/03/17/2964950.html
//功能:求点在有向直线左边还是右边
//返回:0共线、1左边、-1右边
int left_right(point a,point b,double x,double y)
{
double t;
a.x -= x; b.x -= x;
a.y -= y; b.y -= y;
t = a.x*b.y-a.y*b.x;
return t==0 ? 0 : t>0?1:-1;
}
//功能:线段c,d和直线a,b是否相交
bool intersect1(point a,point b,point c,point d)
{
return left_right(a,b,c.x,c.y)^left_right(a,b,d.x,d.y)==-2;
}
//功能:判断线段c,d和线段a,b是否相交
bool intersect(point a,point b,point c,point d)
{
return intersect1(a,b,c,d) && intersect(c,d,a,b);
}
以上是一位大神的!!
//
判断两线段是否相交:
方法(1):快速排斥(两个MBR是否有交集)+跨立(一个线段的两个端点在另一线段的两端)。
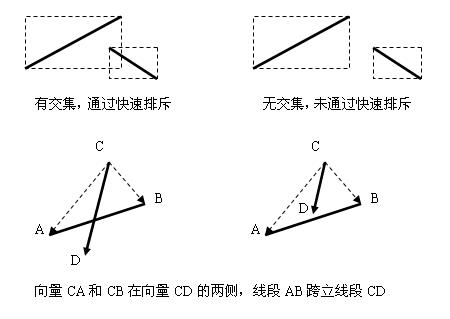
给出C语言代码如下:
/** 由两个点构造一个向量*/
Vector VectorConstruct(Point A, Point B)
{Vector v;v.x = B.x - A.x;v.y = B.y - A.y;return v;
}// 向量的叉积
double CrossProduct(Vector a, Vector b)
{return a.x * b.y - a.y * b.x;
}/** 由两个点构造一个MBR*/
MBR MbrConstruct(Point A, Point B)
{MBR m;if (A.x > B.x){m.xmax = A.x;m.xmin = B.x;}else{m.xmax = B.x;m.xmin = A.x;}if (A.y > B.y){m.ymax = A.y;m.ymin = B.y;}else{m.ymax = B.y;m.ymin = A.y;}return m;
}/** 判断两个MBR是否有交集,有返回1,否0*/
int MbrOverlap(MBR m1, MBR m2)
{double xmin, xmax, ymin, ymax;xmin = Max(m1.xmin, m2.xmin);xmax = Min(m1.xmax, m2.xmax);ymin = Max(m1.ymin, m2.ymin);ymax = Min(m1.ymax, m2.ymax);return (xmax >= xmin && ymax >= ymin) ? 1 : 0;
}/** 判断两线段(线段AB和CD)是否相交,是返回1,否0* 快速排斥+跨立*/
int SegmentIntersection(Point A, Point B, Point C, Point D)
{// (1)判断AB和CD所在的MBR是否相交MBR m1 = MbrConstruct(A, B);MBR m2 = MbrConstruct(C, D);if (MbrOverlap(m1, m2) == 0)return 0;// (2)跨立判断Vector CA = VectorConstruct(C, A);Vector CB = VectorConstruct(C, B);Vector CD = VectorConstruct(C, D);Vector AC = VectorConstruct(A, C);Vector AD = VectorConstruct(A, D);Vector AB = VectorConstruct(A, B);// AB跨立CD,并且,CD跨立ABif (CrossProduct(CD, CA) * CrossProduct(CD, CB) <= 0 && CrossProduct(AC, AB) * CrossProduct(AD, AB) <= 0)return 1;else return 0;
}
方法(2):判断是否为凸多边形。凸多边形的判断是,当从某个点开始绕一周,要么全顺时针拐弯,要么全逆时针。
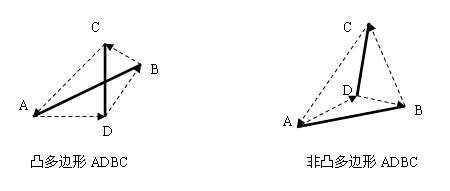
/** 判断两线段(线段AB和CD)是否相交,是返回1,否0* 判断四边形ACBD是否是一个凸四边形*/
int SegmentIntersection(Point A, Point B, Point C, Point D)
{Vector AC = VectorConstruct(A, C);Vector CB = VectorConstruct(C, B);Vector BD = VectorConstruct(B, D);Vector DA = VectorConstruct(D, A);double c[4];c[0] = CrossProduct(AC, CB);c[1] = CrossProduct(CB, BD);c[2] = CrossProduct(BD, DA);c[3] = CrossProduct(DA, AC);int f1=0, f2=0; // 计算正数,负数的个数int i;for (i=0; i<4; i++){if (c[i] > 0) f1++;if (c[i] < 0) f2++;}if (f1 > 0 && f2 > 0) // 有正,有负,返回无交集return 0;elsereturn 1;
}