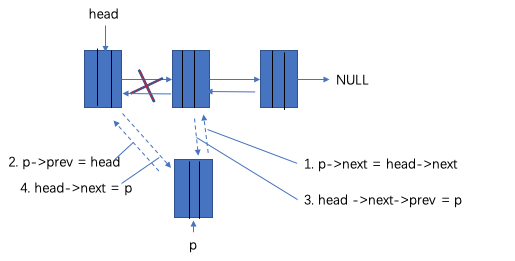
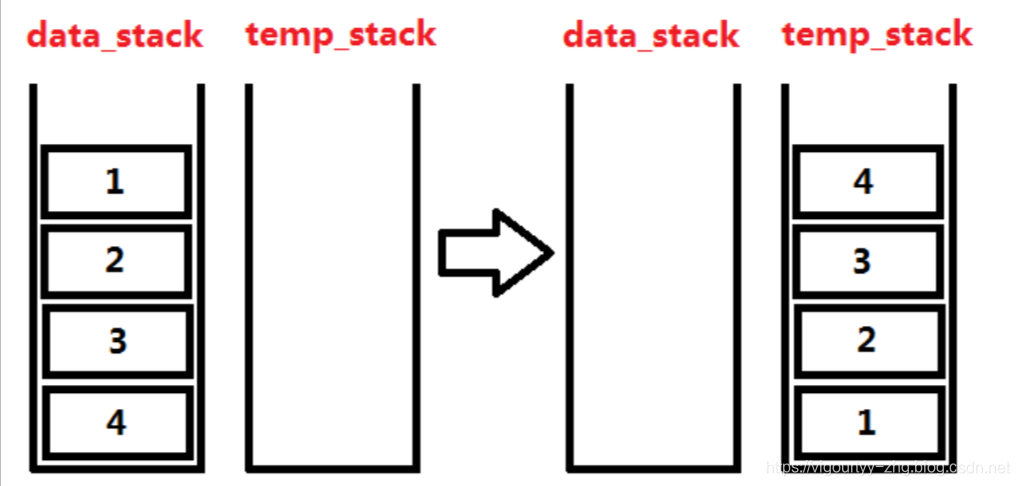
题意:两个数列,第一行的数字可以和第二行的数字连线。连线有如下条件,被连上的两数字必须相等,且每个数字只能连一条线,每条连线必须与且仅与另一条连线相交,相交两连线上的数字不能相等。问最多能连多少条线。
分析:dp。f[i][j]表示第一行的前i个数字和第二行的前j个数字最多能连几条线,则f[i][j]=max(f[i-1][j],f[i][j-1],f[k-1][l-1]+2)。k是第一行前i-1个数字中最右一个能与第二行j位置连线的数的位置。l同理。这样状态转移为n,状态为n^2,总的时间复杂度为n^3。但是我们可以不用每次顺序查找k,l的值,我们进行预处理。数组last_equal1[i][x]表示第一行前i个数字中最右一个等于x的数字的位置。题中说x的取值范围在100以内,所以空间上是可行的。若第一行第i个数恰好是x那么last_equal1[i][x]=i,否则last_equal1[i][x]=last_equal1[i-1][x]。last_equal2[j][x]同理。这样总复杂度降为n^2。

 View Code
View Code #include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> using namespace std;#define maxn 105int n, m; int f[maxn][maxn]; int last_equal1[maxn][maxn], last_equal2[maxn][maxn]; int chain1[maxn], chain2[maxn];void input() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++)scanf("%d", &chain1[i]);for (int i = 1; i <= m; i++)scanf("%d", &chain2[i]); }void make(int n, int chain[], int last_equal[][maxn]) {memset(last_equal, 0, sizeof(last_equal));for (int i = 1; i <= n; i++)for (int j = 1; j <= 100; j++)if (chain[i] == j)last_equal[i][j] = i;elselast_equal[i][j] = last_equal[i - 1][j]; }int work() {make(n, chain1, last_equal1);make(m, chain2, last_equal2);memset(f, 0, sizeof(f));for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++){f[i][j] = max(f[i - 1][j], f[i][j - 1]);int a = chain1[i];int b = chain2[j];int pos1 = last_equal1[i][b];int pos2 = last_equal2[j][a];if (a != b && pos1 != 0 && pos2 != 0)f[i][j] = max(f[i][j], f[pos1 - 1][pos2 - 1] + 1);}return f[n][m] * 2; }int main() {//freopen("t.txt", "r", stdin);int t;scanf("%d", &t);while (t--){input();printf("%d\n", work());}return 0; }