skiplist跳表的 实现
文章目录
- 前言
- 跳表结构
- 时间复杂度
- 空间复杂度
- 高效的动态插入和删除
- 跳表索引的动态更新
- 总结
- 详细实现
前言
rocksdb 的memtable中默认使用跳表数据结构对有序数据进行的管理,为什么呢?
同时redis 也用跳表作为管理自己有序集合的数据结构,为什么他们不选择用红黑树来管理(同样能够提供高效的插入,查找,删除操作,而且各种语言都已经封装好了很多轮子),就选择跳表来实现?
今天就来仔细探讨一下这个数据结构。
跳表结构
对于一个单链表来说,即使链表中存储的数据结构是有序的,想要查找一个元素也需要从头到尾进行查找,时间复杂度是O(n)。

提高查效率的一种办法就是建立索引,对链表建立一级索引,每两个节点提取一个索引节点到上一级,把抽取出来的一级叫做索引。如下图,down就是索引节点指向节点的指针:

此时如果我们想要查找某个节点,比如18。可以先在索引层遍历,当遍历到索引层节点值为13时,发现没有next指针了,此时下降到原始节点层,继续遍历。这个时候只需要遍历一个节点就能访问到数值为18的节点了。
这样的话原来要找节点18,需要遍历8个节点,此时只需要遍历6个节点了,查找效率提高了。那如果我们再增加一级索引,效率会不会更高呢?还是在第一级索引节点的基础上再创建一级索引,如下图:
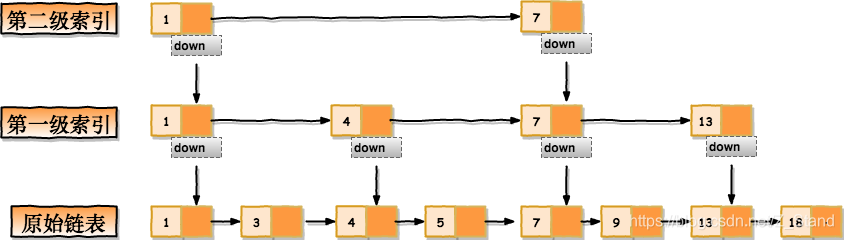
在查找部分节点的情况下效率能够更高,因为这里举例的数据量较小,查看如下数据,有64个原始节点,按照如上的思路建立了五级索引。
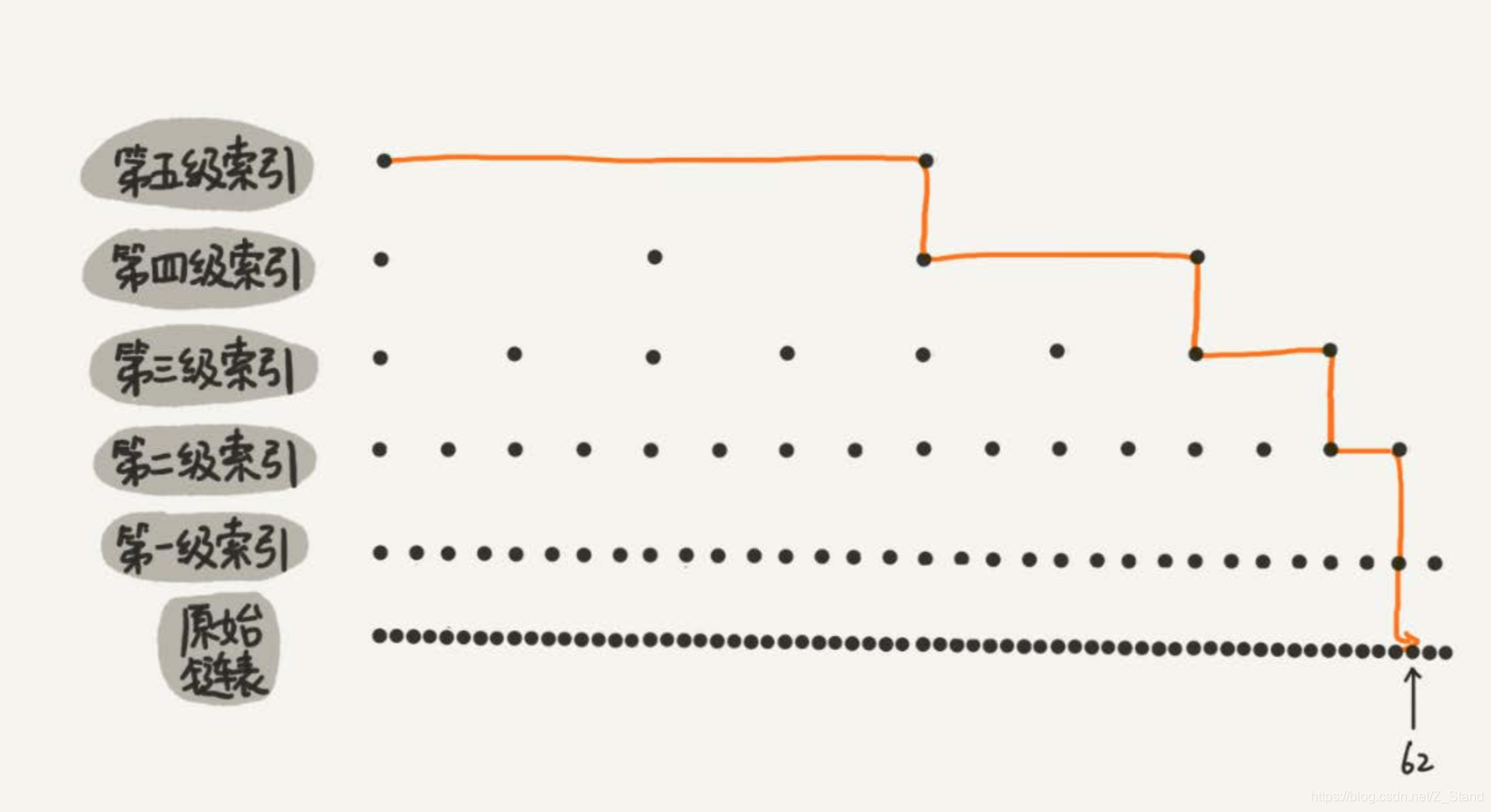
此时查找节点62,原始链表需要遍历62个节点,此时只需要遍历11个节点即可访问到,在数据量较为庞大的情况下效率提升非常明显。
时间复杂度
单链表中查找一个节点的效率是O(n),那么跳表中查找一个节点的时间复杂度是多少呢?
按照我们上面所说,每两个原始节点抽取为一个索引节点的思路。
假设现在有n个节点,每两个节点抽取一个索引节点,那么第一级索引节点的个数:n/2,第二级索引节点:n/4,第三节索引节点:n/8,依次第k级索引节点:n/(2^k)
假设索引有h级,最高级的索引有2个结点。通过上面的公式,我们可以得到n/(2h)=2,从而求得h=log2n-1。如果包含原始链表这一层,整个跳表的高度就是log2n。
我们在跳表中查询某个数据的时候,如果每一层都要遍历m个结点,那在跳表中查询一个数据的时间复杂度就是O(m*logn)。
如何确定m的数值是多少呢,按照上面的索引结构,从最顶层的索引层开始遍历一直到最底层,每一级索引最多需要遍历3个节点。
证明如下:
- 假设我们要查找的数据是x,在第k级索引中
- 遍历到y结点之后,发现x大于y,小于后面的结点z,所以我们通过y的down指针,从第k级索引下降到第k-1级索 引
- 在第k-1级索引中,y和z之间只有3个结点(包含y和z),即我们在K-1级索引中最多只需要遍历3个结点,依次类推,每一级索引都最多只需要遍历3个结 点。
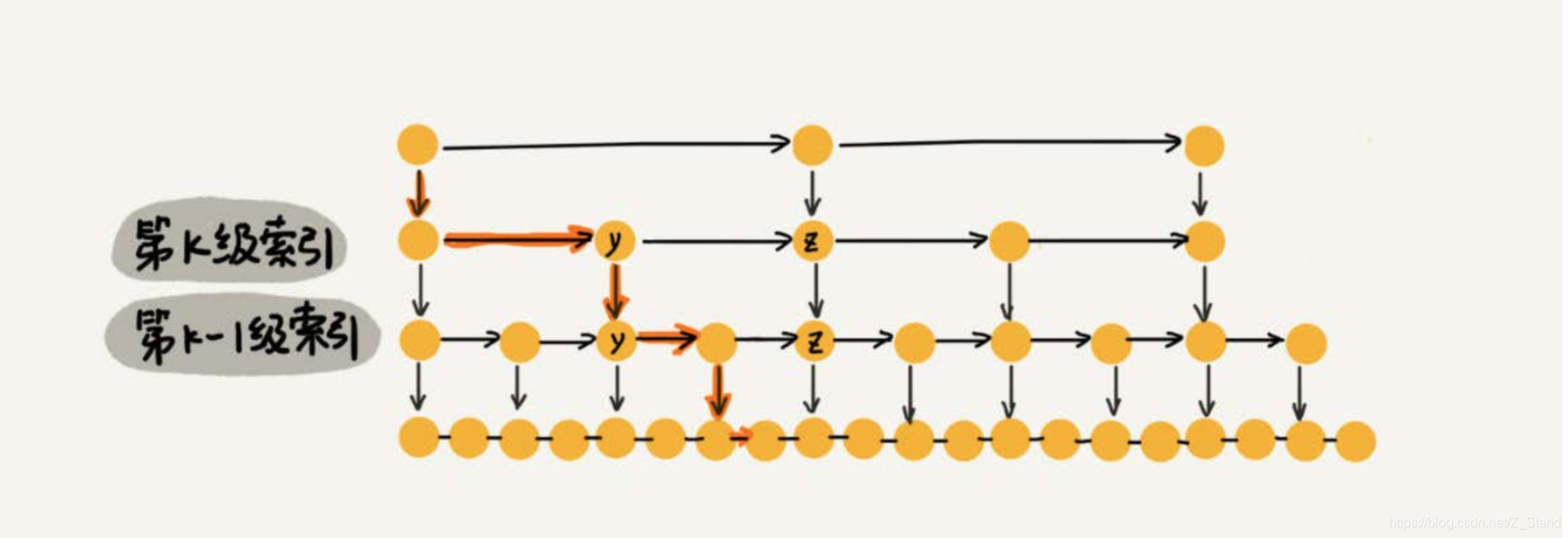
所以我们可以得到m=3这样的一个结论,则在跳表中查询任意一个节点的时间复杂度都为O(logn),效率和二分查找一样。
但是问题也很明显,索引节点消耗内存空间,这是以空间换时间的方式来达到优化的目的,接下来我们看看空间的消耗
空间复杂度
假设原始链表大小为n,我们前面也说过之上的索引节点的个数依次为:
第一级索引节点的个数:n/2,第二级索引节点:n/4,第三节索引节点:n/8,依次第k级索引节点:n/(2^k),直到剩下两个索引节点
这几级索引节点的总和:n/2 + n/4 + n/8 +… 8 + 4 +2 = n -2
可以看出跳表的空间复杂度是O(n)。也就是说,如果将包含n个结点的单链表构造成跳表,我们需要额外再用 接近n个结点的存储空间。那我们有没有办法降低索引占用的内存空间呢?
之前我们是每两个节点抽取一个索引节点,同样我们可以每三个节点抽取一个索引节点,示意图如下:
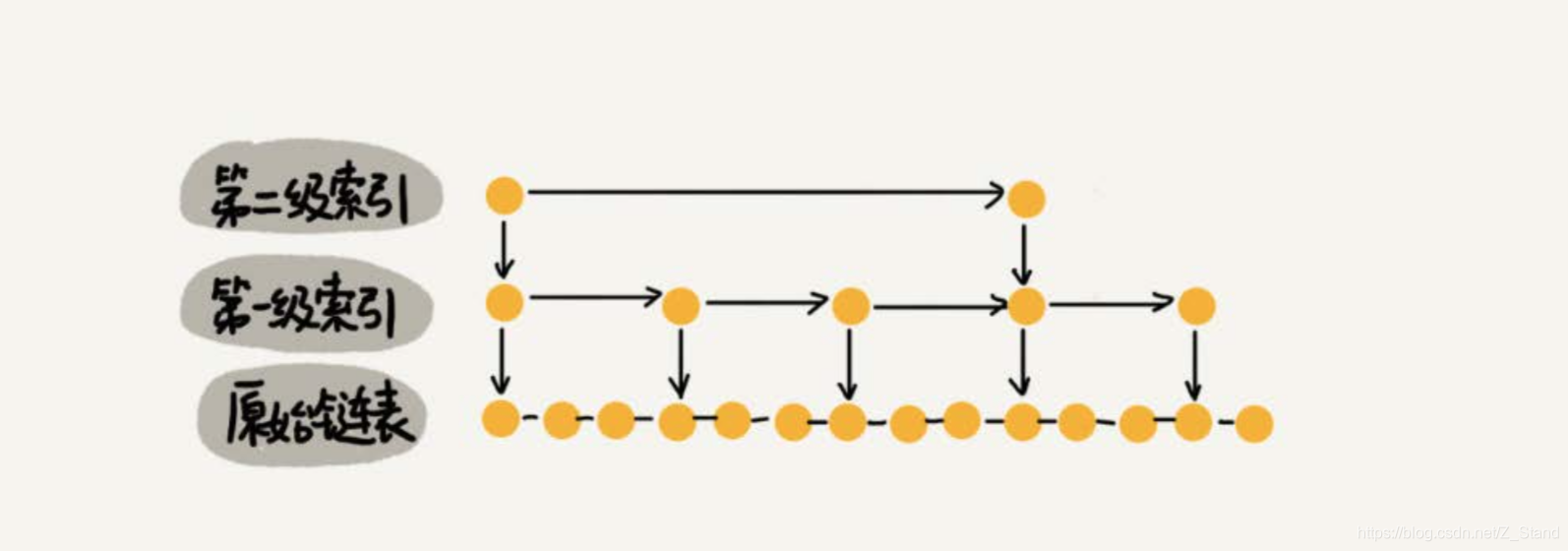
依次总的索引节点的个数为:n/3 + n/9 + n/27 +… + 9 + 3 = n /2
虽然还是O(n)的空间复杂度,但是整体比上面的抽取方式少占用一般的空间。且实际开发过程中,原始链表中存储的大都是数据量庞大的数据,索引节点仅仅存储一些关键数据以及指针,基本的空间消耗并不会很大,可以忽略不计得。
高效的动态插入和删除
插入数据和查找数据的时间复杂度一样,单链表的插入性能消耗O(n)在查找插入位置上,而真正的插入只需要O(1)的时间。同样,跳表的插入也是消耗在查找的时间复杂度上O(logn)。
删除的时候,我们在找到原始链表中的节点之后,如果该节点还出现在索引节点之中,我们除了要删除原始链表中的节点,还需要删除索引层中的节点。
跳表索引的动态更新
当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某2个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。
如下这种情况:
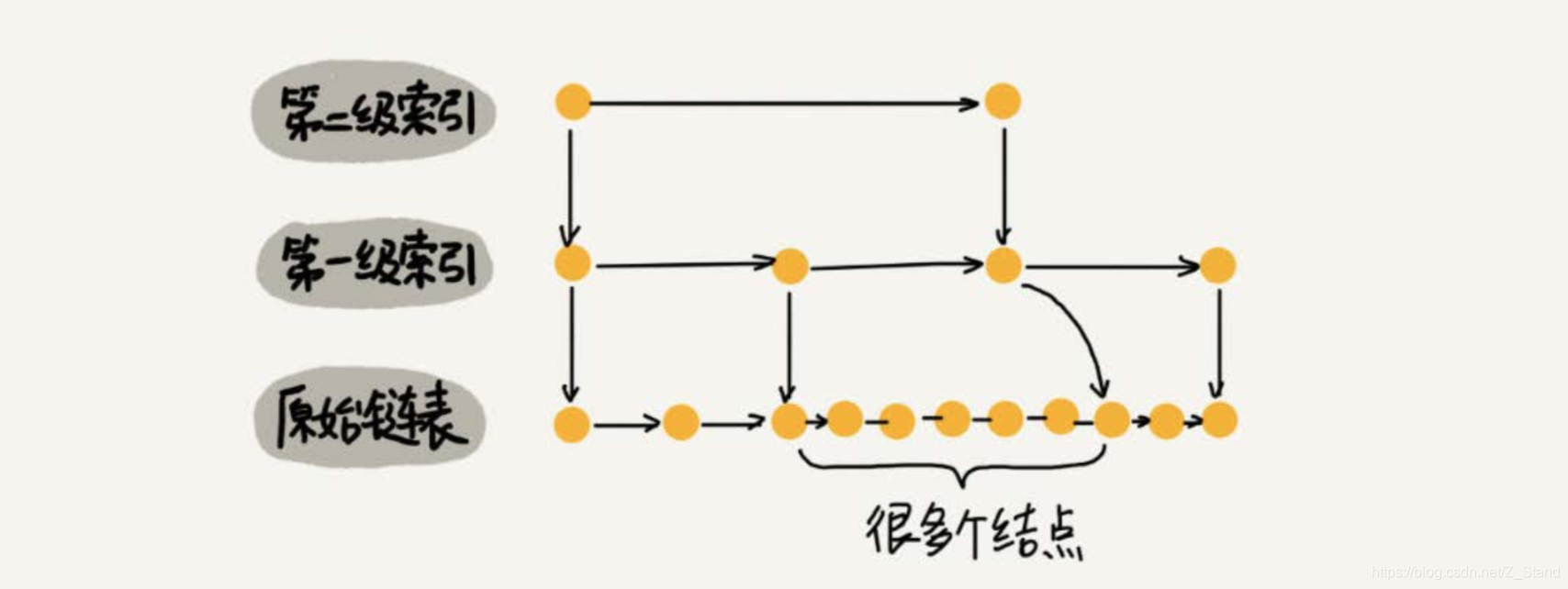
红黑树、AVL树这样平衡二叉树,它们是通过左右旋的方式保持左右子树的大小平衡(如果不了解也没关系,我们后面会讲),而跳表是通 过随机函数来维护前面提到的“平衡性”。
过程如下:
- 通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了K
- 查找当前节点要插入的原始节点的位置
- 基于该位置,从原始链表层向上,每层建立一个指向该节点的down指针,直到第K层
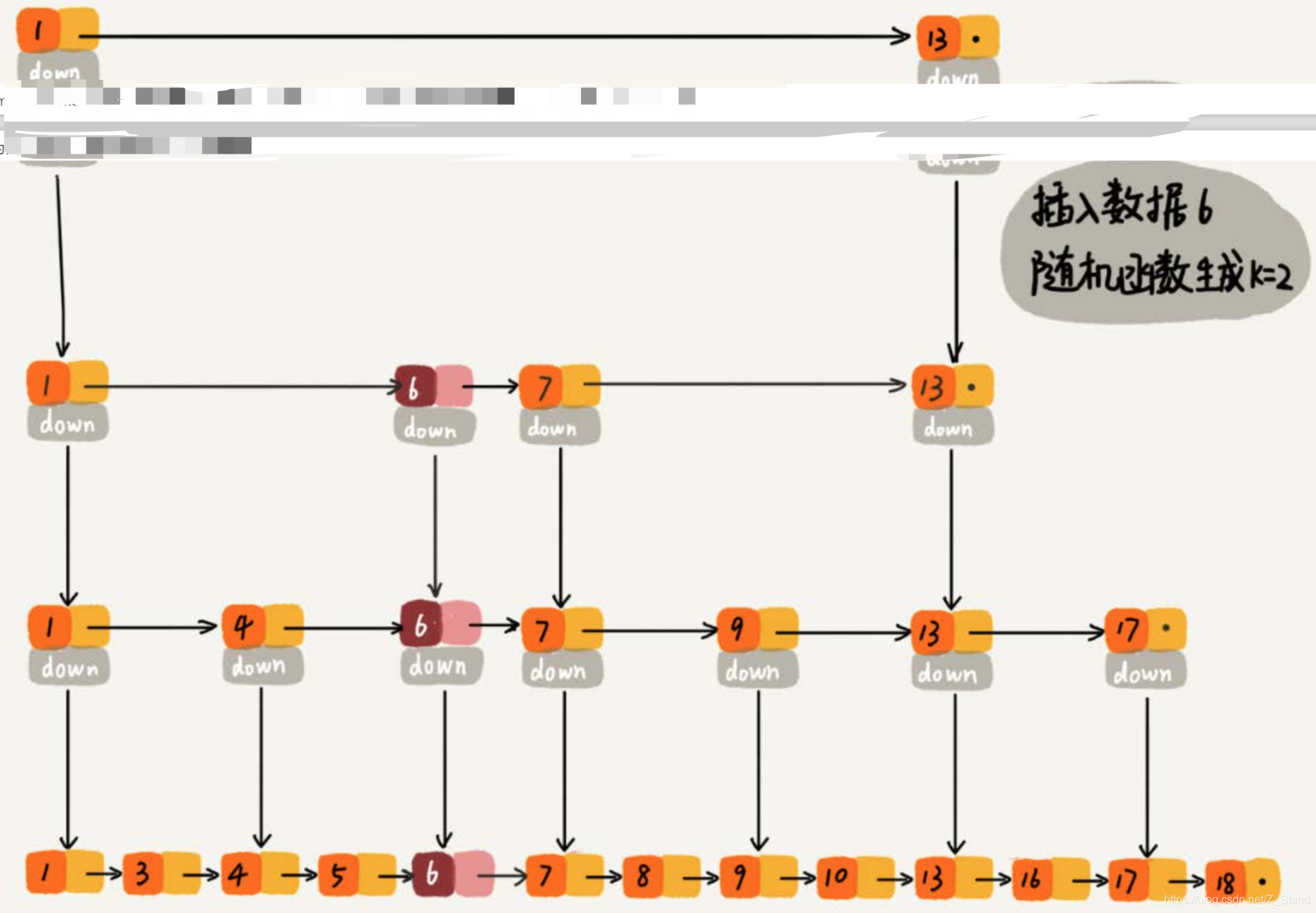
如下节点6 插入该跳表,并且随机函数生成的K=2,即对6创建索引节点直到第二层
总结
综上描述,我们了解了跳表的查找,插入,删除,更新的过程,为什么rocksdb和redis都想要使用跳表作为自己的有序集合的管理结构呢?
像redis和rocksdb 都提供以下核心的数据操作:
- 插入一个数据
- 删除一个数据
- 查找一个数据
- 查找一个区间数据[52,100]
- 不断输出一个有序序列
以上插入,查找,删除,迭代输出的操作跳表和红黑树的效率接近,但是range查找则红黑树没有跳表高
在区间查找的时候,跳表只需要找到区间的第一个元素即可顺序遍历即可(元素是有序的),但是红黑树每一个元素都需要相同的复杂度。
但是跳表并没有红黑树的接口通用,很多语言都提供红黑树的实现接口,跳表还需要自己实现。
详细实现
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string>
#include <cstring>
#include <random>
#include <ctime>
using namespace std;/*** 跳表的一种实现方法。* 跳表中存储的是正整数,并且存储的是不重复的。* * 跳表结构:* * 第K级 1 9* 第K-1级 1 5 9* 第K-2级 1 3 5 7 9* ... ....* 第0级(原始链表) 1 2 3 4 5 6 7 8 9*/const int MAX_LEVEL = 16;/*** @brief 节点
*/
class CNode
{
public:CNode();~CNode();std::string toString();/*** @brief 获取索引链表*/CNode** GetIdxList();/*** @brief 设置数据*/void SetData(int v);/*** @brief 获取数据*/int GetData();/*** @brief 设置最大索引级别*/void SetLevel(int l);
private:/**当前节点的值*/int m_data;/** * 当前节点的每个等级的下一个节点.* 第2级 N1 N2* 第1级 N1 N2* 如果N1是本节点,则 m_lpForwards[x] 保存的是N2* * [0] 就是原始链表.*/CNode* m_lpForwards[MAX_LEVEL];/**当前节点的所在的最大索引级别*/int m_iMaxLevel;
};/*** @brief 跳表
*/
class CSkipList
{
public:CSkipList();~CSkipList();/*** @brief 查找指定的值的节点* @param v 正整数*/CNode* Find(int v);/*** @brief 插入指定的值* @param v 正整数*/void Insert(int v);/*** @brief 删除指定的值的节点* @param v 正整数*/int Delete(int v);void PrintAll();/*** @brief 打印跳表结构* @param l 等于-1时打印所有级别的结构 >=0时打印指定级别的结构*/void PrintAll(int l);/*** @brief 插入节点时,得到插入K级的随机函数* @return K*/int RandomLevel();private:int levelCount;/*** 链表* 带头/哨所(节点)*/CNode* m_lpHead;
};int main()
{CSkipList skipList;/// 插入原始值for(int i=1; i< 50; i++){if((i%3) == 0){skipList.Insert(i);}}for(int i=1; i< 50; i++){if((i%3) == 1){skipList.Insert(i);}}skipList.PrintAll();std::cout<<std::endl;// 打印所有等级结构skipList.PrintAll(-1);// 查找std::cout<<std::endl;CNode* lpNode = skipList.Find(27);if(NULL != lpNode){std::cout<<"查找值为27的节点,找到该节点,节点值:"<<lpNode->GetData()<<std::endl;}else{std::cout<<"查找值为27的节点,未找到该节点"<<std::endl;}/// 删除std::cout<<std::endl;int ret = skipList.Delete(46);if(0 == ret){std::cout<<"查找值为46的节点,找到该节点,并删除成功"<<std::endl;}else{std::cout<<"查找值为46的节点,找到该节点,删除失败"<<std::endl;}std::cout<<std::endl;//打印所有等级结构skipList.PrintAll(-1);std::cin.ignore();return 0;
}CNode::CNode()
{m_data = -1;m_iMaxLevel = 0;for(int i=0; i<MAX_LEVEL; i++){m_lpForwards[i] = NULL;}
}
CNode::~CNode()
{}
CNode** CNode::GetIdxList()
{return m_lpForwards;
}void CNode::SetData(int v)
{m_data = v;
}
int CNode::GetData()
{return m_data;
}
void CNode::SetLevel(int l)
{m_iMaxLevel = l;
}
std::string CNode::toString()
{char tmp[32];std::string ret;ret.append("{ data: ");sprintf(tmp, "%d", m_data);ret.append(tmp);ret.append("; levels: ");sprintf(tmp, "%d", m_iMaxLevel);ret.append(tmp);ret.append(" }");return ret;
}CSkipList::CSkipList()
{levelCount = 1;m_lpHead = new CNode();
}
CSkipList::~CSkipList()
{}
CNode* CSkipList::Find(int v)
{CNode* lpNode = m_lpHead;/*** 从 最大级索引链表开始查找.* K -> k-1 -> k-2 ...->0*/for(int i=levelCount-1; i>=0; --i){/*** 查找小于v的节点(lpNode).*/while((NULL != lpNode->GetIdxList()[i]) && (lpNode->GetIdxList()[i]->GetData() < v)){lpNode = lpNode->GetIdxList()[i];}}/*** lpNode 是小于v的节点, lpNode的下一个节点就等于或大于v的节点*/if((NULL != lpNode->GetIdxList()[0]) && (lpNode->GetIdxList()[0]->GetData() == v)){return lpNode->GetIdxList()[0];}return NULL;
}
void CSkipList::Insert(int v)
{/// 新节点CNode* lpNewNode = new CNode();if(NULL == lpNewNode){return;}/*** 新节点最大分布在的索引链表的上限* 如果返回 3,则 新的节点会在索引1、2、3上的链表都存在*/int level = RandomLevel();lpNewNode->SetData(v);lpNewNode->SetLevel(level);/*** 临时索引链表* 主要是得到新的节点在每个索引链表上的位置*/CNode *lpUpdateNode[level];for(int i=0; i<level; i++){/// 每个索引链表的头节点lpUpdateNode[i] =m_lpHead;}CNode* lpFind = m_lpHead;for(int i= level-1; i >= 0; --i){/*** 查找位置* eg. 第1级 1 7 10* 如果插入的是 6* lpFind->GetIdxList()[i]->GetData() : 表示节点lpFind在第1级索引的下一个节点的数据* 当 "lpFind->GetIdxList()[i]->GetData() < v"不成立的时候,* 新节点就要插入到 lpFind节点的后面, lpFind->GetIdxList()[i] 节点的前面* 即在这里 lpFind就是1 lpFind->GetIdxList()[i] 就是7*/while((NULL != lpFind->GetIdxList()[i]) && (lpFind->GetIdxList()[i]->GetData() < v)){lpFind = lpFind->GetIdxList()[i];}/// lpFind 是新节点在 第i级索引链表的后一个节点lpUpdateNode[i] = lpFind;}for(int i=0; i<level; ++i){/*** 重新设置链表指针位置* eg 第1级索引 1 7 10* 插入6.* lpUpdateNode[i] 节点是1; lpUpdateNode[i]->GetIdxList()[i]节点是7* * 这2句代码就是 把6放在 1和7之间*/lpNewNode->GetIdxList()[i] = lpUpdateNode[i]->GetIdxList()[i];lpUpdateNode[i]->GetIdxList()[i] = lpNewNode;}if(levelCount < level){levelCount = level;}
}
int CSkipList::Delete(int v)
{int ret = -1;CNode *lpUpdateNode[levelCount];CNode *lpFind = m_lpHead;for(int i=levelCount-1; i>= 0; --i){/*** 查找小于v的节点(lpFind).*/while((NULL != lpFind->GetIdxList()[i]) && (lpFind->GetIdxList()[i]->GetData() < v)){lpFind = lpFind->GetIdxList()[i];}lpUpdateNode[i] = lpFind;}/*** lpFind 是小于v的节点, lpFind的下一个节点就等于或大于v的节点*/if((NULL != lpFind->GetIdxList()[0]) && (lpFind->GetIdxList()[0]->GetData() == v)){for(int i=levelCount-1; i>=0; --i){if((NULL != lpUpdateNode[i]->GetIdxList()[i]) && (v == lpUpdateNode[i]->GetIdxList()[i]->GetData())){lpUpdateNode[i]->GetIdxList()[i] = lpUpdateNode[i]->GetIdxList()[i]->GetIdxList()[i];ret = 0;}}}return ret;
}
void CSkipList::PrintAll()
{CNode* lpNode = m_lpHead;while(NULL != lpNode->GetIdxList()[0]){std::cout<<lpNode->GetIdxList()[0]->toString().data()<<std::endl;lpNode = lpNode->GetIdxList()[0];}
}
void CSkipList::PrintAll(int l)
{for(int i=MAX_LEVEL-1; i>=0;--i){CNode* lpNode = m_lpHead;std::cout<<"第"<<i<<"级:"<<std::endl;if((l < 0) || ((l >= 0) && (l == i))){while(NULL != lpNode->GetIdxList()[i]){std::cout<<lpNode->GetIdxList()[i]->GetData()<<" ";lpNode = lpNode->GetIdxList()[i];}std::cout<<std::endl;if(l >= 0){break;}}}
}
int GetRandom()
{static int _count = 1;std::default_random_engine generator(time(0) + _count);std::uniform_int_distribution<int> distribution(1,99999/*0x7FFFFFFF*/);int dice_roll = distribution(generator);_count += 100;return dice_roll;
}
int CSkipList::RandomLevel()
{int level = 1;for(int i=1; i<MAX_LEVEL; ++i){if(1 == (GetRandom()%3)){level++;}}return level;
}
相关文章:

php的反射作用是什么意思,php反射的作用是什么
反射是在PHP运行状态中,扩展分析PHP程序,导出或提取出关于类、方法、属性、参数等的详细信息,包括注释。这种动态获取的信息以及动态调用对象的方法的功能称为反射API。反射是操纵面向对象范型中元模型的API,其功能十分强大&#…
《BI项目笔记》用Excel2013连接和浏览OLAP多维数据集
《BI项目笔记》用Excel2013连接和浏览OLAP多维数据集 原文:《BI项目笔记》用Excel2013连接和浏览OLAP多维数据集用Excel2013连接和浏览OLAP多维数据集 posted on 2014-12-02 08:58 NET未来之路 阅读(...) 评论(...) 编辑 收藏 转载于:https://www.cnblogs.com/lonelyxmas/p/413…

mac 拷贝文件时报错 8060 解决方案
解决如下: 即某文件夹下出现多重子目录,级数很多,删除多余的子文件夹即可。 至于如何产生的,有人说是xcode升级导致,不过没有见证 。我的不属于这类情况的。 (参见:http://macosx.com/forums/ma…

C#连接数据库
VScode 配置C#环境 https://blog.csdn.net/qq_40346899/article/details/80955788VScode 配置C#开发环境 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;using System.Data; using System.Data.SqlCli…

C++ 中emplace_back和push_back差异
前言 最近看rocskdb源码,发现了大量的设计模式和C高级特性,特此补充一下,巩固基础。 问题描述 其中关于动态数组的元素添加,代码中基本将push_back抛弃掉了,全部替换为emplace_back进行元素的添加。 看了一下官网描…
[51单片机学习笔记ONE]-----LED灯的多种使用方法
一.交替闪烁8个LED灯,时间间隔为1s 1 /******************************************************2 实验名称: 交替闪烁8个LED灯,时间间隔1s3 实验时间: 2014年12月2日4 ******************************************************/…
php 伪协议 lfi,php://伪协议(I/O)总能给你惊喜——Bugku CTF-welcome to bugkuctf
今天一大早BugkuCTF 的welcome to bugkuctf 就给了我一发暴击:完全不会啊。。。光看源码就发现不知道怎么处理了,于是转向writeup求助。结果发现这是一道非常有营养的题目,赶紧记录一下。题目链接:http://123.206.87.240:8006/tes…

Pascal's Triangle
帕斯卡三角形,主要考察vector的用法。 vector<vector<int> > generate(int numRows){vector<vector<int> > result;vector<int> tmp;result.clear();tmp.clear();int i,j;if(numRows 0)return result;else if(numRows 1){tmp.push_…
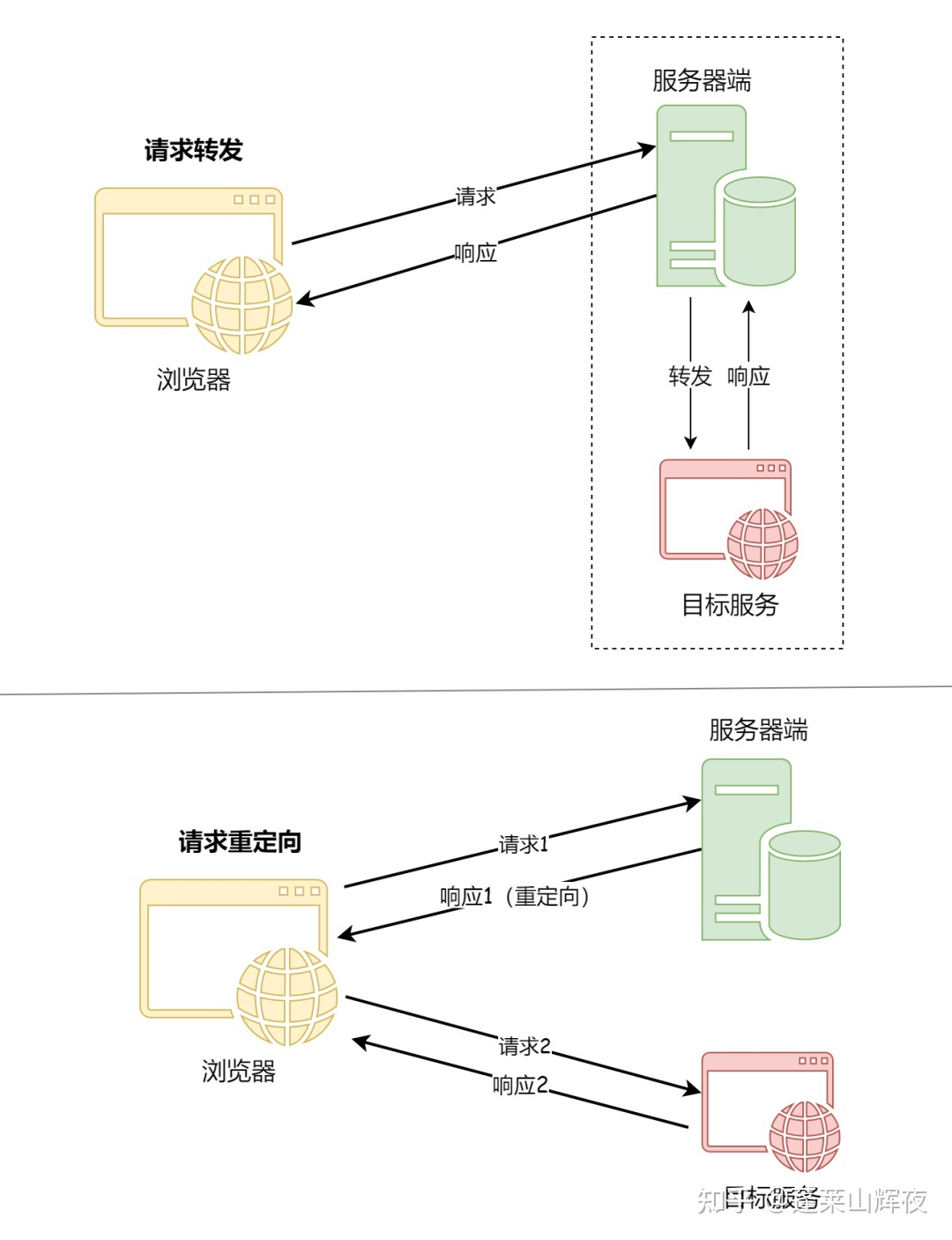
SpringBoot请求转发与重定向
但是可能由于B网址相对于A网址过于复杂,这样搜索引擎就会觉得网址A对用户更加友好,因而在重定向之后任然显示旧的网址A,但是显示网址B的内容。在平常使用手机的过程当中,有时候会发现网页上会有浮动的窗口,或者访问的页面不是正常的页面,这就可能是运营商通过某种方式篡改了用户正常访问的页面。重定向,是指在Nginx中,重定向是指通过修改URL地址,将客户端的请求重定向到另一个URL地址的过程,Nginx中实现重定向的方式有多种,比如使用rewrite模块、return指令等。使用场景:在返回视图的前面加上。

SSO 单点登录和 OAuth2.0 有何区别?
此方法的缺点是它依赖于浏览器和会话状态,对于分布式或者微服务系统而言,可能需要在服务端做会话共享,但是服务端会话共享效率比较低,这不是一个好的方案。在单点登录的上下文中,OAuth 可以用作一个中介,用户在一个“授权服务器”上登录,并获得一个访问令牌,该令牌可以用于访问其他“资源服务器”上的资源。首先,SSO 主要关注用户在多个应用程序和服务之间的无缝切换和保持登录状态的问题。这种方法通过将登录认证和业务系统分离,使用独立的登录中心,实现了在登录中心登录后,所有相关的业务系统都能免登录访问资源。

【转】linux服务器性能查看
转载自https://blog.csdn.net/achenyuan/article/details/78974729 1.1 cpu性能查看 1、查看物理cpu个数: cat /proc/cpuinfo |grep "physical id"|sort|uniq|wc -l 2、查看每个物理cpu中的core个数: cat /proc/cpuinfo |grep "cpu cores…
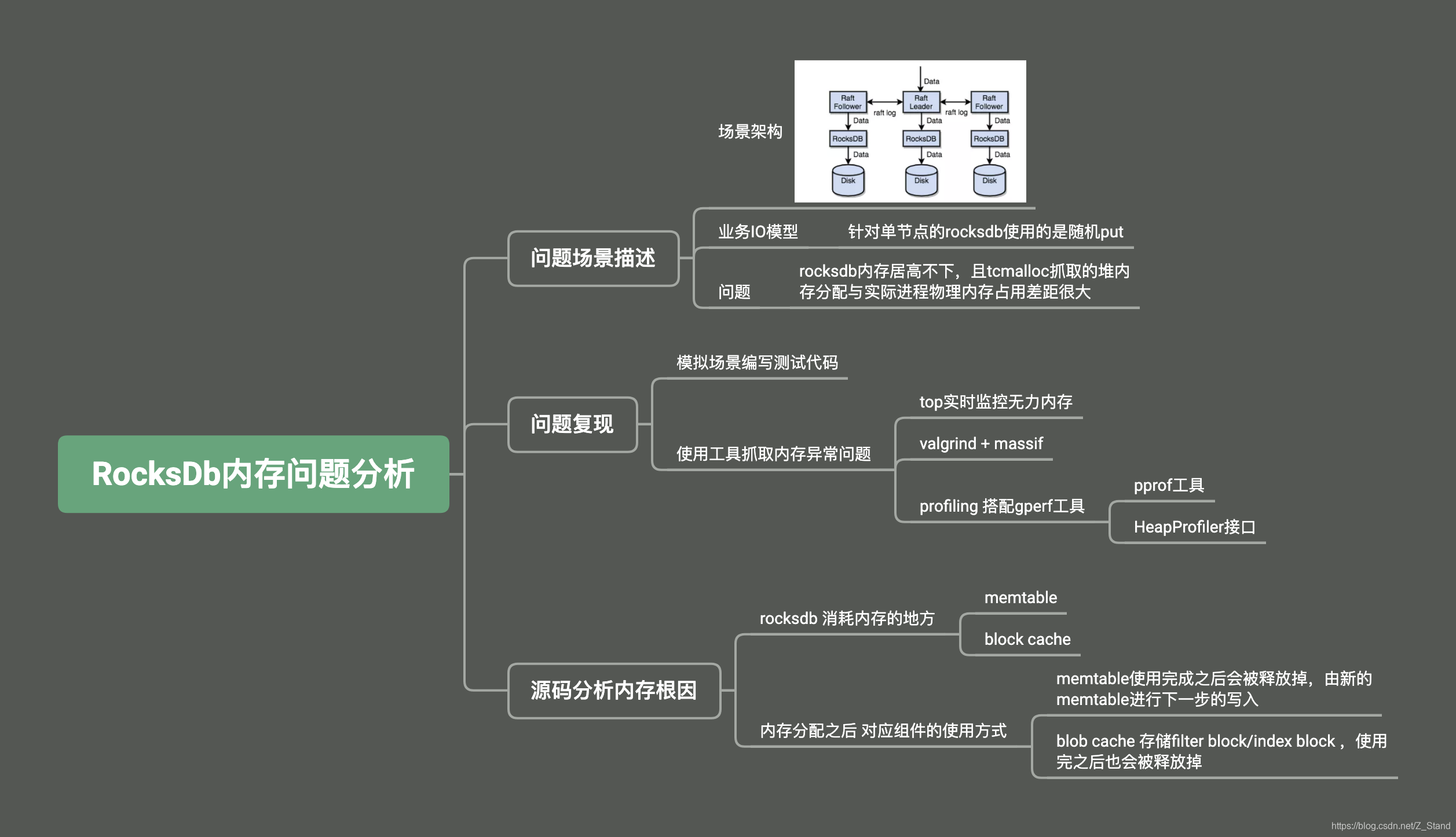
Rocksdb 内存“不释放”问题 分析
文章目录问题场景描述问题复现编写随机写 测试工具使用工具抓取内存分配过程源码分析memtable逻辑table_cache逻辑总结整体的IO场景到底层的源码分析过程如上导图,接下来将详细阐述具体的过程。问题场景描述 我们的rocksdb作为单机存储引擎,跑在用分布式…

GitHub上整理的一些工具【转载】
技术站点Hacker News:非常棒的针对编程的链接聚合网站Programming reddit:同上MSDN:微软相关的官方技术集中地,主要是文档类infoq:企业级应用,关注软件开发领域OSChina:开源技术社区,…

show在php,show.php
我的留言板function dodel(id){if(confirm("确定要删除么?")){window.location del.php?idid;}}我的留言板添加留言查看留言查看留言留言标题留言人留言内容IP地址留言时间操作// 获取留言信息,解析后输出到表格中// 1.从留言liuyan.txt中获取…

#天天复制,今天写一个# 把文字转为图片
/*** 把文字转为图片* * param text* 要写的内容* throws IOException*/public static void textToImg(String text) throws IOException {int len text.length();int fontSize 1000;int width len * fontSize;Font font new Font("楷体", Font2D.NAT…

spark(3) - scala独立编程
>>非集成: 环境需要 * spark 2.4.0 * scala 2.11.12 * sbt (打包) 开发过程 1、shell命令下创建项目目录结构 *****/ project / src / main / scala -> . / ClassName.scala ( touch gedit 命令) …
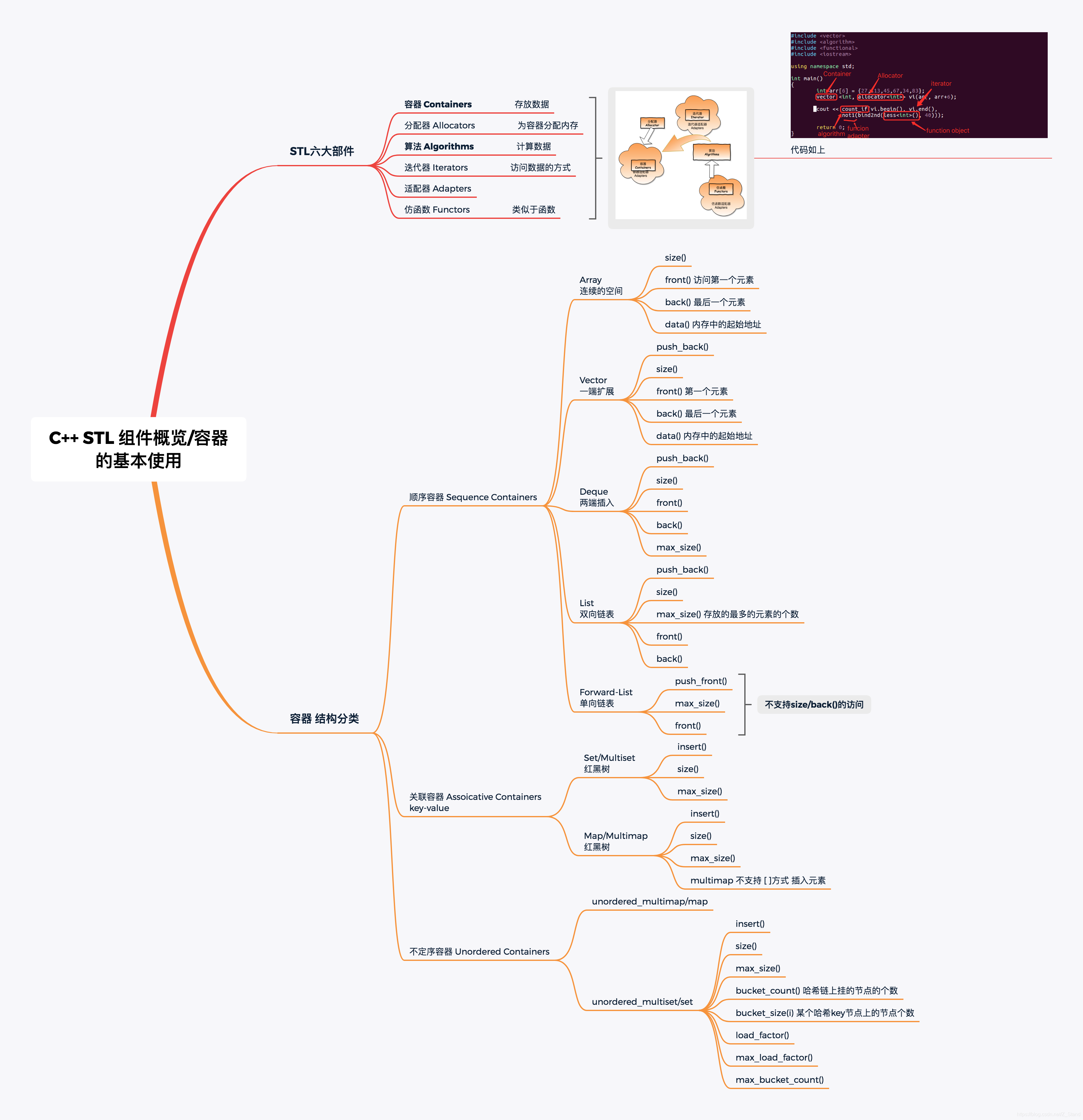
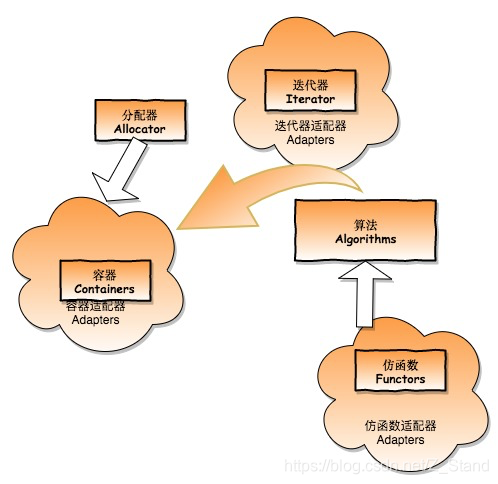
C++ STL: 基本六大部件概览 及 各个容器使用方式和底层实现概览
文章目录STL六大部件容器的使用Arrayvectorlistdequemutisetmultimapunordered_multiset/set使用一个东西,却不明白它的道理,不高明。STL六大部件 容器 Containers 用来存放数据分配器 Allocators 为容器内的数据分配存储空间算法 Algorithms 计算数据迭…

Android窗口管理服务WindowManagerService计算窗口Z轴位置的过程分析
文章转载至CSDN社区罗升阳的安卓之旅,原文地址:http://blog.csdn.net/luoshengyang/article/details/8570428 通过前面几篇文章的学习,我们知道了在 Android系统中,无论是普通的Activity窗口,还是特殊的输入法窗口和壁…

oracle非归档模式下如何备份,Oracle之RMAN数据库在非归档模式下的备份和恢复
1.数据库在非归档模式下的备份 SQLgt; archive log list;数据库日志模式 非存档模式自动存档 禁用存档终点 USE_DB_RECOVERY_FIL1.数据库在非归档模式下的备份SQL> archive log list;数据库日志模式 非存档模式自动存档 禁用存档终点 USE_DB_RECOVERY_FILE_DEST最早的联机日…
C# 视频多人脸识别的实现
上一篇内容的调整,提交到git了,https://github.com/catzhou2002/ArcFaceDemo基本思路如下:一、识别线程1.获取当前图片2.识别当前图片的人脸位置,并将结果存入列表3.分别获取人脸的特征值并比对,并将结果存入列表4.如果…
C++ STL: 分配器allocators 源码分析
STL 基本的六大组件作用以及功能如下: 可以看到allocator是数据存储组件container的幕后支持者,负责为其数据存储分配对应的存储空间。 operator::new 在详细介绍alloctor之前,先描述一下new运算符,我们使用C new一个对象的时候…

android xUtils的使用
gethub地址:https://github.com/wyouflf/xUtils/ xUtils简介 xUtils 包含了很多实用的android工具。xUtils 支持大文件上传,更全面的http请求协议支持(10种谓词),拥有更加灵活的ORM,更多的事件注解支持且不受混淆影响...xUitls 最…
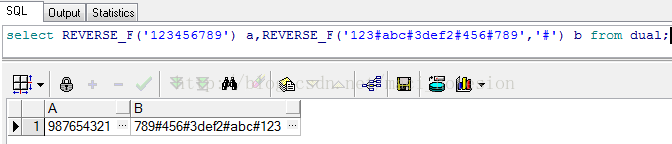
oracle 条件反转,Oracle反转倒置函数
Oracle提供了一个反转倒置函数reverse,但此函数不能分组倒置,本文提供了一个即可分组倒置的函数,如下所示:CREATE OR REPLACE FUNCTION REVERSE_F(p_str VARCHAR2, p_delimiter VARCHAR2:)RETURN VARCHAR2 ISv_return VARCHAR2(40…

android读取大图片并缓存
最近开发电视版的云存储应用,要求”我的相册“模块有全屏预览图片的功能,全屏分辨率是1920*1080超清。UI组件方面采用GalleryImageSwitcher组合,这里略过,详情参见google Android API。相册图片预取缓存策略是内存缓存(…

[ZJOI2018]历史
Description: 给定一棵树,定义每个点的操作为把这个点到1号点的路径覆盖上颜色i,每次该点到1号点经过的不同颜色段数会加到答案中,要使所有点按某一顺序操作完后答案最大 给定每个点要执行的操作次数,并给出m次修改,问每次修改后的最大答案 Hint: \(n,m \le 4*10^5\) Solution:…

C++ STL: lower_bound 和 upper_bound
接口声明 以下有两个不同的版本 lower_bound template <class ForwardIterator, class T>ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,const T& val);template <class ForwardIterator, class T, class Compare>ForwardItera…

1199: 房间安排
1199: 房间安排 Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 1 Solved: 1[Submit][Status][Web Board]Description 2010年上海世界博览会(Expo2010),是第41届世界博览会。于2010年5月1日至10月31日期间,在中国上海市举行。本次世博会也是由中国举办的首届世界…

oracle判断非空并拼接,oracle sql 判断字段非空,数据不重复,插入多跳数据
oracle sql 判断字段非空,数据不重复select distinct(mobile) from wx_user_mobile where active_time is not nullbegininsert into sms_submit(id,gateway_id,source_number,dest_number,message_content)values(sms_system.nextval,1,88…

量产工具介绍(2)
前面介绍了量产工具概念,U盘构造,量产工具获取途径,以及国内的芯片分类,今天,我们从注意事项及常见问题继续介绍量产相关知识注意事项厂家推出的量产工具也是在不断提高版本的,新版本添加有新主控型号驱动。…
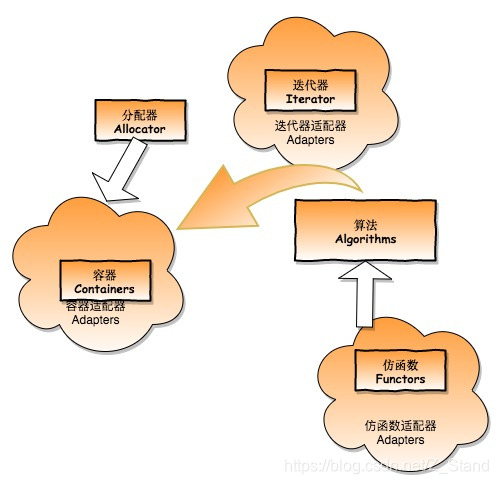
C++ STL: 容器vector源码分析
文章目录前言vector的核心接口vector push_back实现vector 的 Allocatorvector 的 push_back总结前言 vector 是我们CSTL中经常使用的一个容器,提供容量可以动态增长,并且随机访问内部元素的数据存储功能。 这个容器我们最常使用,所以也是最…
