关于 并查集(union find) 算法基本原理 以及 其 在分布式图场景的应用
二月的最后一篇水文…想写一些有意思的东西。
文章目录
- 环检测在图数据结构中的应用
- 深度/广度优先 检测环
- 并查集数据结构 (Union-Find)
- 基本概念
- 初始化
- 合并 union
- 查找祖先
- 优化1: 合并过程 利用 rank 优化路径
- 优化2: 路径压缩(Path Compression)
- 并查集 解决图中检测环问题
环检测在图数据结构中的应用
我们在图数据结构场景中会有一些判断是否存在环的需求,大多数的判断场景是在有向图中:
- 比如我们在图数据存储场景中想要拓扑好友关系,比如查找某一个人到另一个人的好友关系链,这个检索过程需要是一个有向无环图的检索过程,是不能出现环的,需要在检索过程中能够检测到环的存在。
- 再比如 我们在分布式事务场景中,比如悲观事务的实现中往往需要有一个 单key 事务锁 在并发场景的 wait 锁关系的构造 Rocksb 事务锁实现 – 死锁检测部分,这个时候需要对多个事务的 wait锁 之间的互相等待关系构造一个 wait-circle,并且需要在一个元素插入之后检测改有向图是否存在环,存在则需要回退这次的插入。
当然,实际应用到图存储/计算的场景还有很多,对环的检测需求也都是一直存在的。
深度/广度优先 检测环
在这种场景下我们一般检测环存在的做法是遍历图,主要使用两种方式 (bfs/dfs) :
这两种实现方式都比较简单,利用一个visited 数组保证访问过程中除非遇到环,否则不会访问到自己。
下面这个有向图在遍历的过程中会出现环,在分布式事务的场景下 wait-circle 就是出现死锁了,这种情况下是必须要检测出环的。
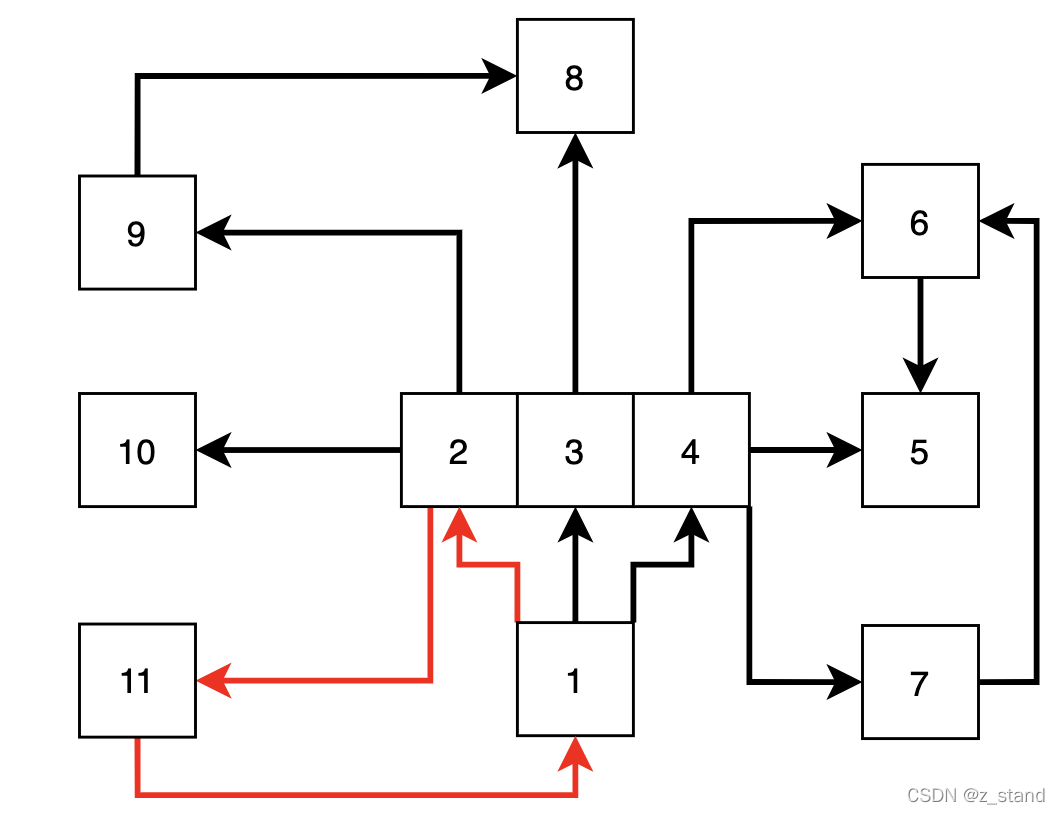
如下使用深度优先搜索来进行环的查找,前置条件就是使用邻接矩阵来标识图中的顶点,比如坐标[i,j] = 1,标识i --> j 即顶点 i 和顶点 j 连通;为 0 则表示两个顶点不连通。
查找的算法也很简单:
- 增加辅助访问数组 visited,标识顶点 i 被访问过。
- 遍历邻接矩阵 且 visited 为 false 的顶点
- 深度优先搜索 所有以 i 为顶点的 [i,j] = 1 即 i --> j ,i --> k的顶点,如果发现某一个顶点 visited[j]=true,那么就标识已经找到环了,否则继续深度优先查找。
// 通过邻接矩阵 matrix 保存有向图
vector<vector<int>> matrix;
bool isCircle(){// 初始化visit 数组,标识已经访问过的节点int m_size = matrix.size();vector<bool> visited(m_size, false);for (int i = 0;i < m_size; i++) {if (!visited[i]) {// 传入当前访问的下标,访问标识数组,最后就是父节点(上一个访问的节点)// 找到了环,就返回真即可.if (dfs_search(i, visited)) {return true;}}}// 整个矩阵都遍历完成还是没有找到,就认为是无环return false;
}// dfs 查找环
bool dfs_search(int current_idx, vector<bool>& visited) {visited[current_index] = true;// 查找 current_idx 即当前节点的连通节点for (int i = 0;i < matrix[current_idx].size(); i++) {// 如果为1,则标识当前current_idx 指向 i,那么check一下这个指向的节点是否访问过,// 那就是找到环了。if (matrix[current_idx][i] == 1) {if ( visited[i] && i != current_idx) return true;else {if (dfs_search(i, visited)) return true;}}}return false;
}
广度优先算法也很类似(层次遍历),同样是通过visited 辅助数组来实。
和dfs的差异只是利用队列来提前将 current_idx 的所有指向的兄弟节点先添加到队列中,再进行下一层的查找,如下代码。
// 通过邻接矩阵 matrix 保存有向图
vector<vector<int>> matrix;
bool isCircle(){int m_size = matrix.size();vector<bool> visited(m_size, false);// 保存当前访问的顶点for (int i = 0;i < m_size; i ++) {if (!visited[i]) {if (bfs_search(i, visited)) return true;}}return false;
}bool bfs_search(int curr_idx, vector<bool>& visited) {queue<int> qu;qu.push(curr_idx);visited[curr_idx] = true;while (!qu.empty()) {int size = qu.size();// 按层遍历for (int j = 0;j < size; j++) {int curr_idx = qu.front();qu.pop();// 需要将 curr_idx 所有的临接顶点 先check 环是否存在,不存在则添加到queue中for (int k = 0;k < matrix[curr_idx].size(); k++) {if (matrix[curr_idx][k] == 1) {if (curr_idx != k && visited[k]) return true;else {qu.push(k);// 标记 curr_idx --> k 的 k顶点已经被访问过了visited[k] = true;}}}}}return false;
}
以上两种实现方式都是非常基础的图中的环的检测,都是是能够正确得检测出环的存在。
但是性能问题却很明显,每一次的检测都需要对整个图进行一个大的scan,对于一个 m*n 的超大矩阵 (我们普通的分布式图存储集群中往往拥有超过百万/千万级别的顶点和 总数目近万亿的边),在这样的图网络中去检测环,利用上面的方式效率可以说是极低的。当然,现在最通用的解决办法就是限制查找的层数。
索引好友关系列表的话也仅仅只会索引3度的出边列表,在分布式事务中的wait-circle 中也会限制死锁检测的深度;但是当我们想要查找两个无关顶点之间的最短到达路径的时候,这个过程中的环检测避免不了,那有没有更加高效的算法,在不用每次插入一个元素都进行一次全链路遍历检测环呢?
当然有~~~, 聪明的人无处不在,并查集 应运而生。
并查集数据结构 (Union-Find)
基本概念
并查集是一种数据结构,其支持对不相交的集合(disjoint sets)执行如下一些操作:
- makeSet(e) 这是 并查集数据结构中的一个操作,用来将输入的元素 e 插入到一个集合中,并返回包含这个元素e 的集合的根节点。
- Union(A,B) 合并两个集合 A,B
- Find(e) 返回包含元素e 的集合
基本概念其实是很晦涩的,直接来看并查集的这几个操作就好。
并查集中的集合元素组织有两种形态:链表形态 和 树形态。
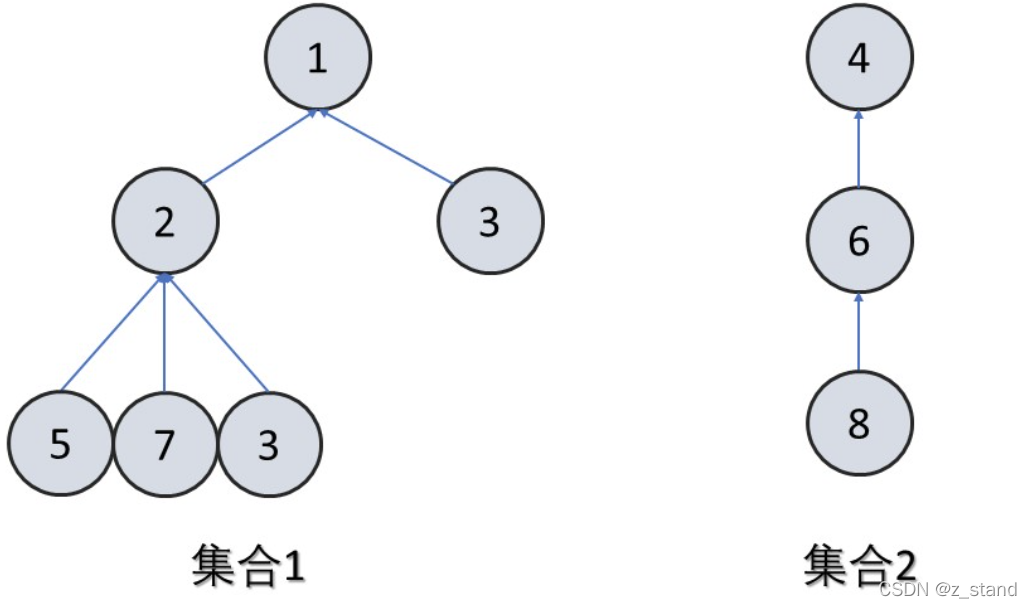
原本我们的链表/树 形态,会记录 parent–>child 或者 prev --> next 这样的关系,而并查集中对数据集的标识 是记录 next 的 prev节点 或者说 是记录 child 的 parent 节点信息。
其中树形态的并查集 表示 方式其实是链表形态的一种优化(路径压缩),能够极大得降低元素查找的层数;当然, 在图的环优化中,这两种形态可以分别用于有向图(链表形态,保存了集合中的方向关系)和 无向图(不需要方向关系)的表示。
接下来,我们看看并查集的每个操作实现。
初始化
对集合中的每一个元素,他们的父节点应该为 空 或者 也可以指向自己(指向自己的这种初始化方式就不能应用在图的环判断中了,可以用于正常的集合操作)。
本文演示均用-1 表示空
虽然前面说并查集的数据结构 有两种形态, 链表或者树,但是实际我们应用的时候,可以采用数组/无序map 的方式就够了。
unorder_map<int,int> father;
void Add(int ele) {if (!father.count(ele)) {father[ele] = -1; }
}
合并 union
这个操作主要是check 两个节点是否可以连通(祖先是不同的), 如果是连通的,那就要进行合并,让他们拥有相同的祖先。
这里两个节点 谁当祖先都是可以的。
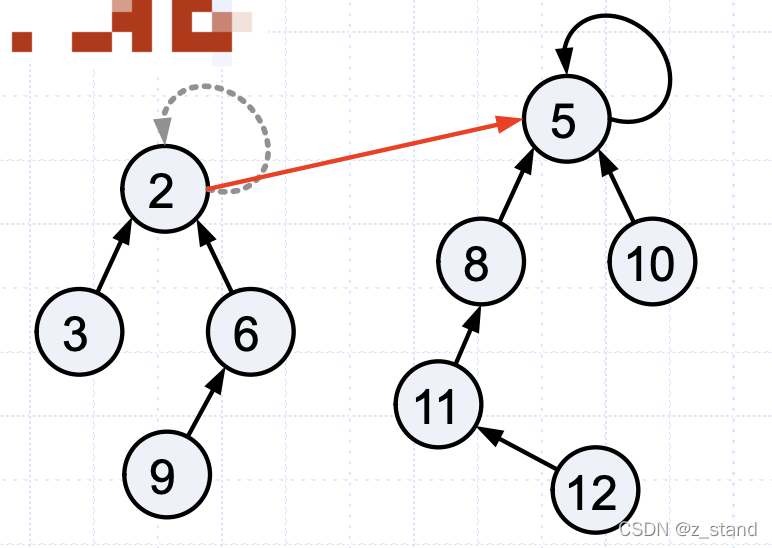
void union(int x, int y) {int x_root = find(x);int y_root = find(y);// 祖先不同,则发现是两个不同的集合,则可以对他们进行合并if (x_root != y_root) {fater[x_root] = y_root;}
}
查找祖先
如果节点的父节点不为空,那就需要持续查找,直到找到父节点为空的节点,就是当前输入的ele 的祖先节点。
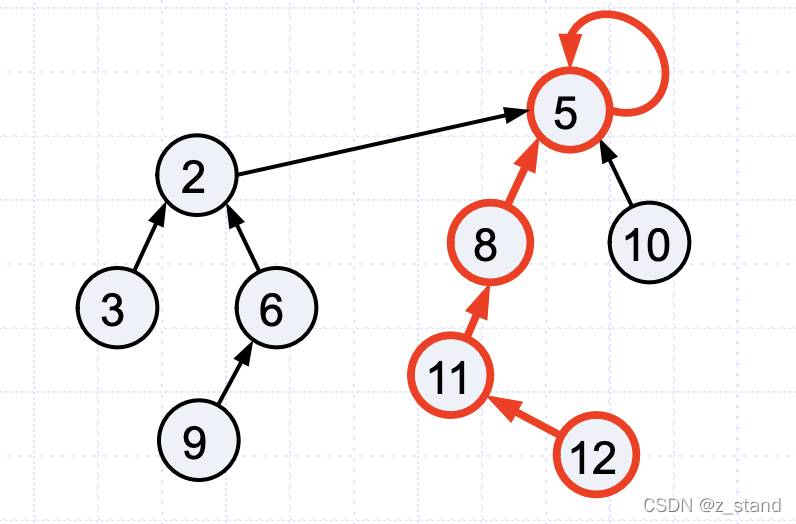
我们想要查找节点 12 的祖先节点,就需要不断的check father节点,直到father节点为空(或者是自己)。
int find(int ele) {int root = ele;while (father[root] != -1) {root = father[root];}return root;
}
这里是有可以优化的地方,我们希望在并查集中的节点分布能够更接近树形态,而不是链表形态。毕竟树形查找的复杂度是小于等于(O(log_n)),也就是我们可以将链表形态的并查集结构转换为树形态。
这样做可行的原因是 对于并查集中的节点来说连通性是可以传递的, 节点之间互相连通的标记只需要拥有一个相同的祖先就好了。
大体过程如下:
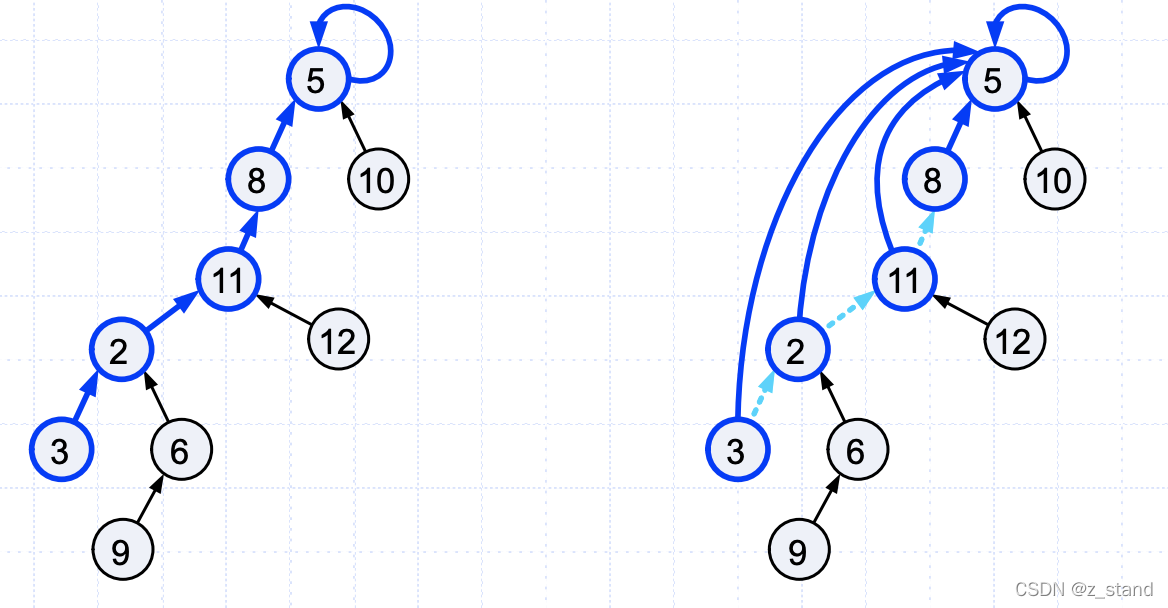
就是将上图中左侧一段链式结构可以合并成右侧的树形结构。
优化1: 合并过程 利用 rank 优化路径
rank 是一个在前面father基础上额外增加的一个数据结构,标识当前节点距离祖先节点的长度,这样我们的初始化以及合并代码就变成下面的样子:
typedef struct UnionFindNode {UnionFindNode* father;int rank;UnionFindNode() : father(nullptr),rank(0) {}bool operator==(const UnionFindNode& lhs) {return father == lhs.father && rank == lhs.rank;}
}Node;void MakeSet(Node& ele) {ele.father = nullptr;ele.rank = 0;
}void Union(const Node x, Node y) {// 找到他们的公共祖先节点auto xRoot = Find(x);auto yRoot = Find(y);if (xRoot == yRoot) {return;}// 他们不在同一个集合,则需要合并他们的祖先。// 将距离比较短的合并到距离长的祖先上。if (xRoot->rank < yRoot->rank) {xRoot->father = yRoot;} else if (xRoot->rank > yRoot->rank) {yRoot->father = xRoot;} else { //rank 相等,互相指向谁都无所谓,需要增加指向后的被指向节点的rank(增加了一个元素的深度)。xRoot->father = yRoot;yRoot->rank += 1;}
}
优化2: 路径压缩(Path Compression)
当然,以上优化方式也能够利用rank 达到我们将链表转换成树的目的,但是需要一个额外的rank 字段,每一个节点都会多消耗4bytes 的内存 。
其实还有一种更简洁优雅的优化方式,就是 路径压缩。
rank 的优化是在 Union 操作的时候,这里路径压缩 则是在 Find的时候。
// 还是继续使用基本的 unorder_map 保留信息
unordered_map<int, int> father;// 查找节点 i 的祖先节点
int Find(int i) {int root = i;// -1 是我们在最前面 Add 一个新的并查集节点的时候// 会将这个节点的父节点设置为 -1,标识它目前是一个单独的集合。while(father[root] != -1) {root = father[root];}// 路径压缩的过程while (i != root) {int origin_father = father[i];father[i] = root;// 关键!进行路径压缩,将节点i 的父节点直接指向祖先节点。i = origin_father;}return root;
}
比如对于这样的一个并查集集合,我们想要查找 6。
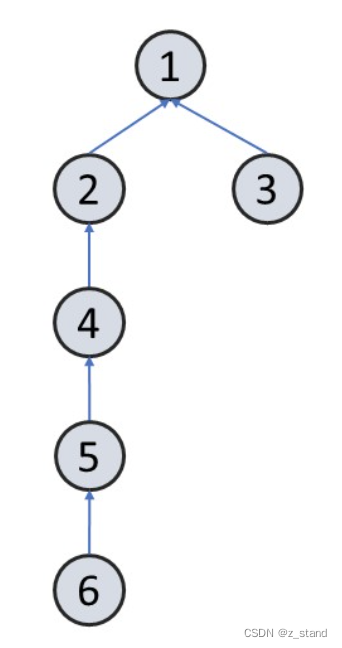
经过路径压缩之后, 6 包括整个之前的节点都会尝试进行一次路径压缩。
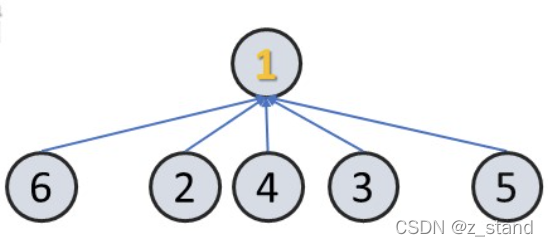
关于路径压缩的时间复杂度证明较为复杂,这个推演是通过 阿克曼函数 进行推演的。
总之表示方式是 O(log*n),其中 log*n表示 n 取多少次 log2nlog_2nlog2n并向下取整之后变成1,可以理解为是 O(1) 级别。
比如 log*2^65526 ,2^65536 在阿克曼函数中表示的是 A(4,3) 的结果,基本是人类思维极限的数字,而 在 log*n 下仅仅只有 5。
关于路径压缩时间复杂度的推演 以及 证明 可以参考 The math in Union-Find.
并查集 解决图中检测环问题
回到我们最初 图中检测环的问题,我们接下来可以利用并查集的几个操作轻松解决。
对于 0 --> 1 --> 2,构造出来的并查集结构 经过路径压缩 是 0 --> 2 <-- 1 ;而如果存在环,也就意味着 2 --> 0,对于并查集来说 我们只需要 提前 find (0) 和 find(2) 是否相等,如果相等,则认为当前的插入是会造成环的(0 已经存在 且 其祖先节点是2)。
实现如下:
class UnionFind {
public:// void Add// void Union// int Find// bool IsConnected
private:unordered_map<int,int> father_;
}
// 通过邻接矩阵 matrix 保存有向图
vector<vector<int>> matrix;
bool IsCircle() {UnionFind uf;for (int i = 0;i < matirx.size(); i++) {// 添加每一个节点到并查集之中uf.Add(i);for (int j = 0;j < i; j++) {if (matrix[i][j]) {int x_root = Find(i);int y_root = Find(j);// 发现了两个不同节点的祖先节点相等,则找到了环if (x_root == y_root && i != j) return true;// 否则,是两个可以连通的节点,那就需要合并这两个集合(他们的祖先直接合并就好了)。if (x_root != y_root) uf.Union(x_root,y_root);}}}return false;
}
通过并查集,我们能够在有节点更新的情况下非常高效得O(1) 的时间内确认这个节点插入后图中是否存在环。
除了检测环之外,并查集在图数据结构的其他方向也有非常高效的应用,比如确认图中两个顶点是否连通,高效合并两组无关联的图等等。
总的来说,并查集这个数据结构 利用阿克曼函数 在集合论 以及 图数据结构领域中 能够非常高效得判断集合交集 以及 图节点连通情况,思想值得学习研究。
相关文章:

Java项目:智能制造生产管理平台(java+SSM+mysql+Maven+Easyui+JSP)
源码获取:博客首页 "资源" 里下载! 运行环境:jdk1.8、tomcat7.0/8.5、Mysql5.7/5.1、Maven3.6/3.5、 eclipse/STS 功能简介:计划进度、设备管理、工艺监控、物料监控、质量监控、人员监控等 访问注册控制层:…

JAVA-Eclipse快捷键
Ctrl1:快速修复。CtrlD:快速删除行。ShiftEnter:快速调到下一行。CtrlF11:快速运行。Alt上下方向键:快速移动。CtrlM:光标所在视图最大化。Alt/:智能补全。Ctrl/:快速注释代码。 转载于:https://www.cnblogs.com/bluewhy/p/44669…

Android RelativeLayout属性
// 相对于给定ID控件android:layout_above 将该控件的底部置于给定ID的控件之上;android:layout_below 将该控件的底部置于给定ID的控件之下;android:layout_toLeftOf 将该控件的右边缘与给定ID的控件左边缘对齐;android:layout_toRightOf 将该控件的左边缘与给定ID的控件右边缘…
详解Azure的权限控制
注意:本文档仅限于Azure国际版,国内版略有不同Azure中的角色分配相对来说是比较复杂的的,对于任何云组织来说,云的资源访问管理权限都是一项非常重要的功能,azure中的授权系统叫做基于角色的访问控制(RBAC&…

SNMP introduction
简单网络管理协议(SNMP)首先是由Internet工程任务组织(Internet Engineering Task Force)(IETF)的研究小组为了解决Internet上的路由器管理问题而提出的。许多人认为 SNMP在IP上运行的原因是Internet运行的是TCP/IP协议,然而事实并不是这样。 SNMP被设计成与协议无…
Java项目:在线考试系统(java+SSM+mysql+JSP)
源码获取:博客首页 "资源" 里下载! 运行环境:jdk1.8、Mysql5.7、Tomcat8.5、IDEA/Eclipse 功能简介:在线考试、历史回顾、个人成绩查询等。 管理员和教师功能有:学院管理、班级管理、课程管理、教师、学生…

Keil中使用宏编译来定义DEBUG输出
使用宏编译来格式化调试信息,是一个不错的方法,即可以在需要的时候打印出信息,还可以格式化我们所需要的输出。 #define DEBUG 1 #if (DEBUG 1) #define DBG(Args...) printf(##Args) #define DBGFL(s, Args...) printf("[%s:%d]&qu…
解决用户使用临时配置文件登陆WIN7的问题
用户登录Win7后,经常会遇到 “您已使用临时配置文件登陆” 的提示,忽略此提示的用户通常在桌面上保留的文件再次重启进入后发现文件丢失了,或者原有桌面上的文件不见了,这样一定程度上降低了工作的效率.这里主要说一下如何解决此问题。用户登…

chosen.jquery.js 有搜索功能、多选功能的下拉框插件
chosen.jquery.js 有搜索功能、多选功能的下拉框插件 官方源码: https://github.com/harvesthq/chosen 该源码中的样例index.html有该插件的详细使用介绍posted on 2019-05-09 14:40 三天打鱼,两天晒网 阅读(...) 评论(...) 编辑 收藏 转载于:https://w…

MIB in SNMP
管理信息库MIB指明了网络元素所维持的变量(即能够被管理进程查询和设置的信息)。MIB给出了一个网络中所有可能的被管理对象的集合的数据结构。SNMP的管理信息库采用和域名系统DNS相似的树型结构,它的根在最上面,根没有名字。图3画…

Java项目:后台管理系统脚手架项目(java+SpringBoot+FreeMarker+mysql+JSP)
源码获取:博客首页 "资源" 里下载! 项目描述: 这是一个基于SpringBoot框架开发的后台管理系统脚手架项目。之所以称为脚手架项目,是因为这个项目复用性很强,如果以后有其他新的项目要设计后台管理系统的话&…

Extjs4.0.7 MVC Architecture异常
uncaught exception: Ext.Loader is not enabled, so dependencies cannot be resolved dynamically. Missing required class: AM.controller.User 解决方法: 在app.js最上面加上:Ext.Loader.setConfig({ enabled: true }); Ext.Loader.setConfig({ …

Mybatis常见面试题(三)
Mybatis 映射文件中,如果 A 标签通过 include 引用了 B 标签的内容,请问, B 标签能否定义在 A 标签的后面,还是说必须定义在 A 标签的前面? :虽然 Mybatis 解析 Xml 映射文件是按照顺序解析的,但是&#x…

SMI in SNMP
SNMP中,数据类型并不多。这里我们就讨论这些数据类型,而不关心这些数据类型在实际中是如何编码的。INTEGER一个变量虽然定义为整型,但也有多种形式。有些整型变量没有范围限制,有些整型变量定义为特定的数值(例如&am…

Java项目:在线拍卖竞价系统(java+SpringBoot+FreeMarker+Mysql+redis)
源码获取:博客首页 "资源" 里下载! 超级管理员:系统管理、用户管理(冻结等)、审批竞拍标的物管理、竞标类型管理、审批机构、个人提现管理(审核)、企业提现管理(审批&…

pig脚本不需要后缀名(python tempfile模块生成pig脚本临时文件,执行)
pig 脚本运行不需要后缀名 pig脚本名为tempfile,无后缀名 用pig -f tempfile 可直接运行 另外,pig tempfile也可以直接运行这样就可以用python临时文件存储pig脚本内容直接调用 python调用pig脚本的一种方式 将pig脚本用任意文件存储,执行时写…

老谢oracle视频笔记_day02
1:databasea:physical structure1:controlfile控制文件select * from v$controlfile;11g 以三个11g二个互为镜像文件坏了数据库就打不开了..IO一个块 16k一个文件2MB不会太大?10MB数据库名数据文件位置很多的参数.....2:datafile 数据文件select file_name,file_id from dba_d…

WCDMA系统中的扰码规划
摘要:宽带码分多址(WCDMA)系统采用码分多址的无线接入方式,不需频率规划,但需进行相邻小区扰码的规划用以区分各小区。通过WCDMA无线网络的扰码规划,可以确定两个使用相同扰码的小区的复用距离,区分各小区。扰码规划时…
Java项目:宿舍寝室维修上报管理系统(java+SpringBoot+FreeMarker+Mysql)
源码获取:博客首页 "资源" 里下载! 管理员:校园管理(楼栋管理、宿舍管理)、师生管理(学生管理、辅导员管理)、维修管理(维修工管理、维修进度管理)、阅览室管理…

项目需求分析与建议
软件名称:私人助手 1.N(需求):当今生活节奏迅速,每个人每天都有许多事情要做,堆积成山的事情往往让人感到迷茫,不知道什么时候要做什么事情。私人助手就是为了解决这个烦恼而产生,它会根据最初你添加的事物…

使用面向 iOS 的本机插件扩展 PhoneGap
本文细致探讨了 Xcode(以 iOS 设备为目标)中的 PhoneGap(也称为 Apache Cordova)应用程序本机插件。如果您刚开始接触 PhoneGap 或者需要回顾 PhoneGap 基础知识,请先阅读 Xcode for iOS 的 PhoneGap 入门,…

算法总结---最常用的五大算法(算法题思路)
算法总结---最常用的五大算法(算法题思路) 一、总结 一句话总结: 【明确所求:dijkstra是求点到点的距离,辅助数组就是源点到目标点的数组】 【最简实例分析:比如思考dijkstra:假设先只有三个点】…

软切换中的测量
软切换中的测量 同频测量: CPICH RSCP、Ec/N0, 事件触发报告,1A,...,1F 1A,相对门限增加事件,表示一个小区的质量已经接近最好小区或者活动集质量 1B,相对门限删除事件,表示一个小区…

测试与封装5.1.5.2
1.第一阶段目标 - 把计算的功能封装成类。2.设计测试用例:用白盒与黑盒测试设计技术,为计算核心设计测试用例。3.在实验环境中(如MyEclipse集成开发环境Junit测试框架)运行测试用例,分析测试结果,找出程序问…

Java项目:企业员工绩效工资管理系统(java+SpringBoot+FreeMarker+Mysql)
源码获取:博客首页 "资源" 里下载! 超级管理员等角色,除基础脚手架外,实现的功能有: 超级管理员:系统管理、用户管理(冻结等)、职称管理、部门管理(工资项&am…

Sql server 阻塞定位
很多人都遇到过这样的情况,当网站达到一定的访问量,数据库就会成为瓶颈,进而引起阻塞。有人认为这可能就是硬件的极限了,于是想办法增加硬件设备。而我本人认为问题的元凶可能是性能不高的sql脚本,引起了阻塞。如果你和…
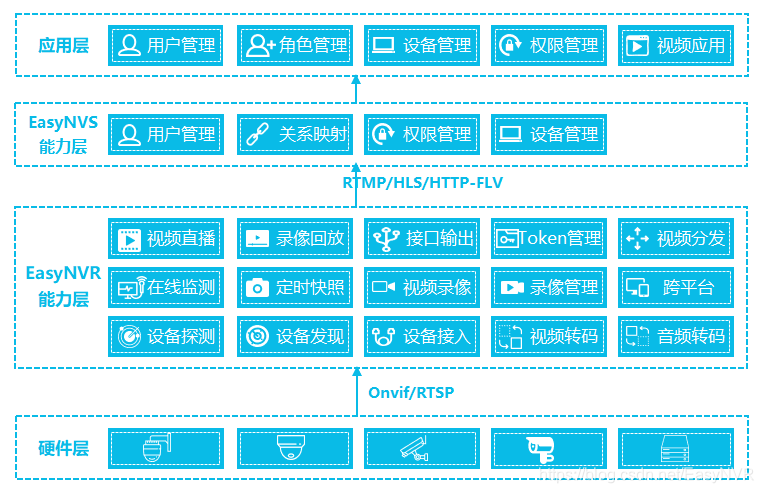
基于EasyNVR摄像机网页无插件直播服务二次开发实现H5播放页面的简单集成方案...
我们通常在构架一套视频SaaS应用的过程中,将平台设计为3层:视频硬件层(视频源)、视频能力平台(vPaaS)、视频应用平台(vSaaS),视频硬件包括各种IPC、NVR、编码器等视频生成…

active set + serving cell
空闲态:这时候手机只能使用一路信号,应该是最强的那一路。手机在空闲态时不断地搜索各个导频的强度,如果搜到比当前使用的导频更强的,那么它就自发的进行切换。这个切换的过程是手机自发的过程,不需要基站的参与。业务…
Java项目:医院分诊挂号住院管理系统(java+SpringBoot+FreeMarker+Mysql)
源码获取:博客首页 "资源" 里下载! 主要实现了从挂号预约到分诊住院出诊等一些列医院基本操作流程的全部功能,系统分医生、患者、管理员三个角色,除基础脚手架外,实现的功能有: 管理员ÿ…

网站压力测试工具webbench
webbench最多可以模拟3万个并发连接去测试网站的负载能力,个人感觉要比Apache自带的ab压力测试工具好,安装使用也特别方便。 1、适用系统:Linux 2、编译安装: 引用wget http://blog.zyan.cc/soft/linux/webbench/webbench-1…
